十四、回归的推断
译者:飞龙
自豪地采用谷歌翻译
到目前为止,我们对变量之间关系的分析纯粹是描述性的。我们知道如何找到穿过散点图的最佳直线来绘制。在所有直线中它的估计的均方误差最小,从这个角度来看,这条线是最好的。
但是,如果我们的数据是更大总体的样本呢?如果我们在样本中发现了两个变量之间的线性关系,那么对于总体也是如此嘛?它会是完全一样的线性关系吗?我们可以预测一个不在我们样本中的新的个体的响应变量吗?
如果我们认为,散点图反映了被绘制的两个变量之间的基本关系,但是并没有完全规定这种关系,那么就会出现这样的推理和预测问题。例如,出生体重与孕期的散点图,显示了我们样本中两个变量之间的精确关系;但是我们可能想知道,对于抽样总体中的所有新生儿或实际中的一般新生儿,这样的关系是否是真实的,或者说几乎是正确的。
一如既往,推断思维起始于仔细检查数据的假设。一组假设被称为模型。大致线性的散点图中的一组随机性的假设称为回归模型。
回归模型
简而言之,这样的模型认为,两个变量之间的底层关系是完全线性的;这条直线是我们想要识别的信号。但是,我们无法清楚地看到这条线。我们看到的是分散在这条线上的点。在每一点上,信号都被随机噪声污染。因此,我们的推断目标是将信号从噪声中分离出来。
更详细地说,回归模型规定了,散点图中的点是随机生成的,如下所示。
x和y之间的关系是完全线性的。我们看不到这个“真实直线”,但它是存在的。- 散点图通过将线上的点垂直移动,或上或下来创建,如下所示:
- 对于每个
x,找到真实直线上的相应点(即信号),然后生成噪声或误差。 - 误差从误差总体中带放回随机抽取,总体是均值为 0 的正态分布。
- 创建一个点,横坐标为
x,纵坐标为“x处的真实高度加上误差”。 - 最后,从散点图中删除真正的线,只显示创建的点。
基于这个散点图,我们应该如何估计真实直线? 我们可以使其穿过散点图的最佳直线是回归线。 所以回归线是真实直线的自然估计。
下面的模拟显示了回归直线与真实直线的距离。 第一个面板显示如何从真实直线生成散点图。 第二个显示我们看到的散点图。 第三个显示穿过散点图的回归线。 第四个显示回归线和真实直线。
为了运行模拟,请使用三个参数调用draw_and_compare函数:真实直线的斜率,真实直线的截距以及样本量。
运行模拟几次,用不同的斜率和截距,以及不同的样本量。 因为所有的点都是根据模型生成的,所以如果样本量适中,你会看到回归线是真实直线的一个良好估计。
# The true line,
# the points created,
# and our estimate of the true line.
# Arguments: true slope, true intercept, number of points
draw_and_compare(4, -5, 10)
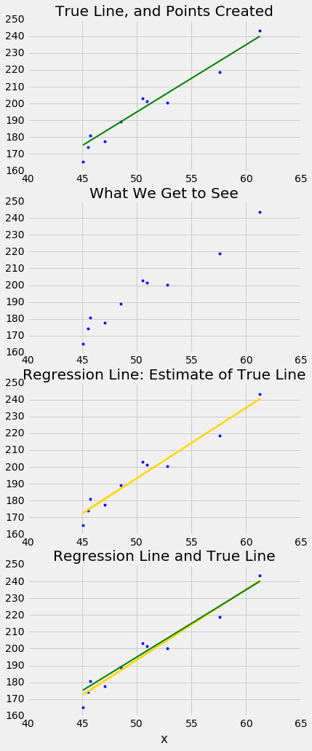
实际上,我们当然不会看到真实直线。 模拟结果表明,如果回归模型看起来合理,并且如果我们拥有大型样本,那么回归线就是真实直线的一个良好近似。
真实斜率的推断
我们的模拟表明,如果回归模型成立,并且样本量很大,则回归线很可能接近真实直线。 这使我们能够估计真实直线的斜率。
我们将使用我们熟悉的母亲和她们的新生儿的样本,来开发估计真实直线的斜率的方法。 首先,我们来看看我们是否相信,回归模型是一系列适当假设,用于描述出生体重和孕期之间的关系。
correlation(baby, 'Gestational Days', 'Birth Weight')
0.40754279338885108
总的来说,散点图看起来相当均匀地分布在这条线上,尽管一些点分布在主云形的周围。 相关系数为 0.4,回归线斜率为正。
这是否反映真实直线斜率为正的事实? 为了回答这个问题,让我们看看我们能否估计真实斜率。 我们当然有了一个估计:我们的回归线斜率。 这大约是 0.47 盎司每天。
slope(baby, 'Gestational Days', 'Birth Weight')
0.46655687694921522
但是如果散点图出现的方式不同,回归线会有所不同,可能会有不同的斜率。 我们如何计算,斜率可能有多么不同?
我们需要点的另一个样本,以便我们可以绘制回归线穿过新的散点图,并找出其斜率。 但另一个样本从哪里得到呢?
你猜对了 - 我们将自举我们的原始样本。 这会给我们自举的散点图,通过它我们可以绘制回归线。
自举散点图
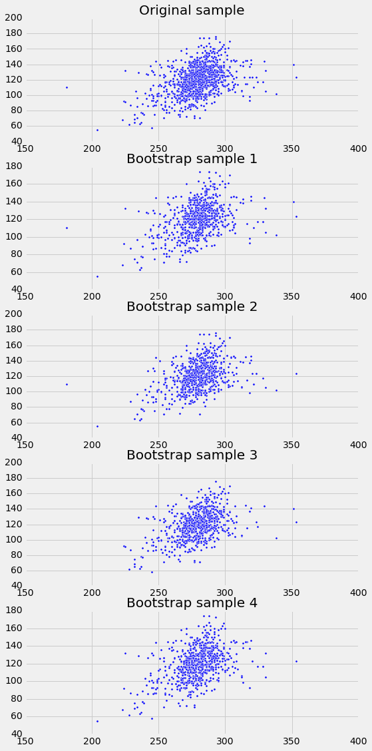
我们可以通过对原始样本带放回地随机抽样,来模拟新样本,它的次数与原始样本量相同。 这些新样本中的每一个都会给我们一个散点图。 我们将这个称为自举散点图,简而言之,我们将调用整个过程来自举散点图。
这里是来自样本的原始散点图,以及自举重采样过程的四个复制品。 请注意,重采样散点图通常比原始图稀疏一点。 这是因为一些原始的点没有在样本中被选中。
估计真实斜率
我们可以多次自举散点图,并绘制穿过每个自举图的回归线。 每条线都有一个斜率。 我们可以简单收集所有的斜率并绘制经验直方图。 回想一下,在默认情况下,sample方法带放回地随机抽取,次数与表中的行数相同。 也就是说,sample默认生成一个自举样本。
slopes = make_array()
for i in np.arange(5000):
bootstrap_sample = baby.sample()
bootstrap_slope = slope(bootstrap_sample, 'Gestational Days', 'Birth Weight')
slopes = np.append(slopes, bootstrap_slope)
Table().with_column('Bootstrap Slopes', slopes).hist(bins=20)
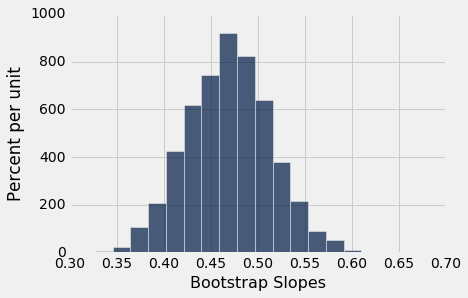
然后,我们可以使用percentile方法,为真实直线的斜率构建约 95% 置信区间。 置信区间从 5000 个自举斜率的第 2.5 百分位数,延伸到第 97.5 百分位数。
left = percentile(2.5, slopes)
right = percentile(97.5, slopes)
left, right
(0.38209399211893086, 0.56014757838023777)
用于自举斜率的函数
让我们收集我们估计斜率的方法的所有步骤,并定义函数bootstrap_slope来执行它们。 它的参数是表的名称,预测变量和响应变量的标签,以及自举复制品的所需数量。 在每个复制品中,该函数自举原始散点图并计算所得回归线的斜率。 然后绘制所有生成的斜率的直方图,并打印由斜率的“中间 95%”组成的区间。
def bootstrap_slope(table, x, y, repetitions):
# For each repetition:
# Bootstrap the scatter, get the slope of the regression line,
# augment the list of generated slopes
slopes = make_array()
for i in np.arange(repetitions):
bootstrap_sample = table.sample()
bootstrap_slope = slope(bootstrap_sample, x, y)
slopes = np.append(slopes, bootstrap_slope)
# Find the endpoints of the 95% confidence interval for the true slope
left = percentile(2.5, slopes)
right = percentile(97.5, slopes)
# Slope of the regression line from the original sample
observed_slope = slope(table, x, y)
# Display results
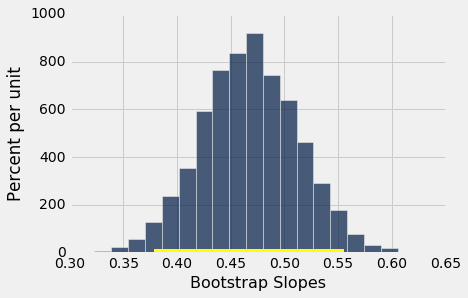
Table().with_column('Bootstrap Slopes', slopes).hist(bins=20)
plots.plot(make_array(left, right), make_array(0, 0), color='yellow', lw=8);
print('Slope of regression line:', observed_slope)
print('Approximate 95%-confidence interval for the true slope:')
print(left, right)
当响应变量为出生体重,预测变量为孕期时,我们调用bootstrap_slope来找到真实斜率的置信区间,我们得到了一个区间,非常接近我们之前获得的东西:大约 0.38 到 0.56 盎司每天。
bootstrap_slope(baby, 'Gestational Days', 'Birth Weight', 5000)
Slope of regression line: 0.466556876949
Approximate 95%-confidence interval for the true slope:
0.378663152966 0.555005146304
现在我们有一个函数,可以自动完成估计在回归模型中展示斜率的过程,我们也可以在其他变量上使用它。
例如,我们来看看出生体重与母亲身高的关系。 更高的女性往往有更重的婴儿吗?
回归模型似乎是合理的,基于散点图,但相关性不高。 这只有大约 0.2。
scatter_fit(baby, 'Maternal Height', 'Birth Weight')
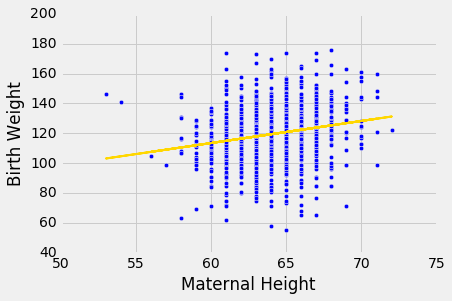
correlation(baby, 'Maternal Height', 'Birth Weight')
0.20370417718968034
像之前一样,我们使用bootstrap_slope来估计回归模型中真实直线的斜率。
bootstrap_slope(baby, 'Maternal Height', 'Birth Weight', 5000)
Slope of regression line: 1.47801935193
Approximate 95%-confidence interval for the true slope:
1.0403083964 1.91576886223
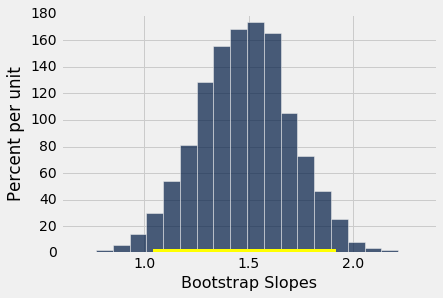
真实斜率的 95% 置信区间,从约 1 延伸到约 1.9 盎司每英寸。
真实斜率可能为 0 嘛?
假设我们相信我们的数据遵循回归模型,并且我们拟合回归线来估计真实直线。 如果回归线不完全是平的,几乎总是如此,我们将观察到散点图中的一些线性关联。
但是,如果这种观察是假的呢? 换句话说,如果真实直线是平的 - 也就是说,这两个变量之间没有线性关系 - 我们观察到的联系,只是由于从样本中产生点的随机性。
这是一个模拟,说明了为什么会出现这个问题。 我们将再次调用draw_and_compare函数,这次要求真实斜率为 0。我们的目标是,观察我们的回归线是否显示不为 0 的斜率。
请记住函数draw_and_compare的参数是真实直线的斜率和截距,以及要生成的点的数量。
draw_and_compare(0, 10, 25)

运行模拟几次,每次保持真实直线的斜率为 0 。你会注意到,虽然真实直线的斜率为 0,但回归线的斜率通常不为 0。回归线有时会向上倾斜,有时会向下倾斜,每次都给我们错误的印象,即这两个变量是相关的。
为了确定我们所看到的斜率是否真实,我们想测试以下假设:
原假设。真实直线的斜率是 0。
备选假设。真实直线的斜率不是 0。
我们很有条件来实现它。由于我们可以为真实斜率构建一个 95% 的置信区间,我们所要做的就是看区间是否包含 0。
如果没有,那么我们可以拒绝原假设(P 值为 5% 的截断值)。
如果真实斜率的置信区间确实包含 0,那么我们没有足够的证据来拒绝原假设。也许我们看到的斜率是假的。
我们在一个例子中使用这个方法。假设我们试图根据母亲的年龄来估计新生儿的出生体重。根据样本,根据母亲年龄估计出生体重的回归线的斜率为正,约为 0.08 盎司每年。
slope(baby, 'Maternal Age', 'Birth Weight')
0.085007669415825132
虽然斜率为正,但是很小。 回归线非常接近平的,这就产生了一个问题,真实直线是否是平的。
scatter_fit(baby, 'Maternal Age', 'Birth Weight')

我们可以使用bootstrap_slope来估计真实直线的斜率。 计算表明,真实斜率的约 95% 的自举置信区间左端为负,右端为正 - 换句话说,区间包含 0。
bootstrap_slope(baby, 'Maternal Age', 'Birth Weight', 5000)
Slope of regression line: 0.0850076694158
Approximate 95%-confidence interval for the true slope:
-0.104335243815 0.272791852339
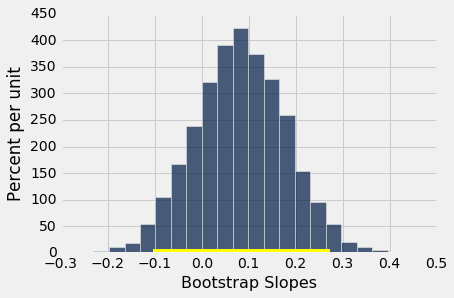
因为区间包含 0,所以我们不能拒绝原假设,母亲年龄与新生儿出生体重之间的真实线性关系的斜率为 0。基于此分析,使用母亲年龄作为预测变量,基于回归模型预测出生体重是不明智的。
预测区间
回归的主要用途之一是对新个体进行预测,这个个体不是我们原始样本的一部分,但是与样本个体相似。在模型的语言中,我们想要估计新值x的y。
我们的估计是真实直线在x处的高度。当然,我们不知道真实直线。我们使用我们的样本点的回归线来代替。
给定值x的拟合值,是基于x值的y的回归估计。换句话说,给定值x的拟合值就是回归线在x处的高度。
假设我们试图根据孕期天数来预测新生儿的出生体重。我们在前面的章节中看到,这些数据非常适合回归模型,真实直线的斜率的 95% 置信区间不包含 0。因此,我们的预测似乎是合理的。
下图显示了预测位于回归线上的位置。红线是x = 300。
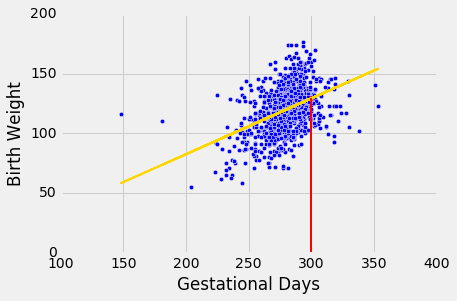
红线与回归线的相交点的高度是孕期天数 300 的拟合值。
函数fitted_value计算这个高度。像函数的相关性,斜率和截距一样,它的参数是表的名称和x和y的列标签。但是它也需要第四个参数,即x的值,在这个值上进行估算。
def fitted_value(table, x, y, given_x):
a = slope(table, x, y)
b = intercept(table, x, y)
return a * given_x + b
孕期天数 300 的拟合值约为 129.2 盎司。 换句话说,对于孕期为 300 天的孕妇,我们估计的新生儿体重约为 129.2 盎司。
fit_300 = fitted_value(baby, 'Gestational Days', 'Birth Weight', 300)
fit_300
129.2129241703143
预测的可变性
我们已经开发了一种方法,使用我们样本中的数据,根据孕期天数预测新生儿的体重。 但作为数据科学家,我们知道样本可能有所不同。 如果样本不同,回归线也会不一样,我们的预测也是。 为了看看我们的预测有多好,我们必须了解预测的可变性。
为此,我们必须生成新的样本。 我们可以像上一节那样,通过自举散点图来实现。 然后,我们为每个散点图的复制品拟合回归线,并根据每一行进行预测。 下图显示了 10 条这样的线,以及孕期天数 300 对应的出生体重预测。
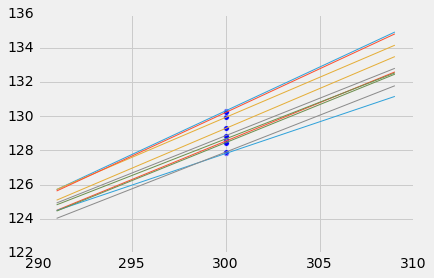
lines
| slope | intercept | prediction at x=300 |
|---|---|---|
| 0.503931 | -21.6998 | 129.479 |
| 0.53227 | -29.5647 | 130.116 |
| 0.518771 | -25.363 | 130.268 |
| 0.430556 | -1.06812 | 128.099 |
| 0.470229 | -11.7611 | 129.308 |
| 0.48713 | -16.5314 | 129.608 |
| 0.51241 | -23.2954 | 130.428 |
| 0.52473 | -27.2053 | 130.214 |
| 0.409943 | 5.22652 | 128.21 |
| 0.468065 | -11.6967 | 128.723 |
每一行的预测都不相同。 下表显示了 10 条线的斜率、截距以及预测。
自举预测区间
如果我们增加重采样过程的重复次数,我们可以生成预测的经验直方图。这将允许我们创建预测区间,使用为斜率创建自举置信区间时的相同的百分比方法。
让我们定义一个名为bootstrap_prediction的函数来实现。该函数有五个参数:
- 表的名称
- 预测变量和响应变量的列标签
- 用于预测的
x的值 - 所需的自举重复次数
在每次重复中,函数将自举原始散点图,并基于x的指定值查找y的预测值。具体来说,它调用我们在本节前面定义的函数fitted_value,来寻找指定x处的拟合值。
最后,绘制所有预测值的经验直方图,并打印由预测值的“中间 95%”组成的区间。它还打印基于穿过原始散点图的回归线的预测值。
# Bootstrap prediction of variable y at new_x
# Data contained in table; prediction by regression of y based on x
# repetitions = number of bootstrap replications of the original scatter plot
def bootstrap_prediction(table, x, y, new_x, repetitions):
# For each repetition:
# Bootstrap the scatter;
# get the regression prediction at new_x;
# augment the predictions list
predictions = make_array()
for i in np.arange(repetitions):
bootstrap_sample = table.sample()
bootstrap_prediction = fitted_value(bootstrap_sample, x, y, new_x)
predictions = np.append(predictions, bootstrap_prediction)
# Find the ends of the approximate 95% prediction interval
left = percentile(2.5, predictions)
right = percentile(97.5, predictions)
# Prediction based on original sample
original = fitted_value(table, x, y, new_x)
# Display results
Table().with_column('Prediction', predictions).hist(bins=20)
plots.xlabel('predictions at x='+str(new_x))
plots.plot(make_array(left, right), make_array(0, 0), color='yellow', lw=8);
print('Height of regression line at x='+str(new_x)+':', original)
print('Approximate 95%-confidence interval:')
print(left, right)
bootstrap_prediction(baby, 'Gestational Days', 'Birth Weight', 300, 5000)
Height of regression line at x=300: 129.21292417
Approximate 95%-confidence interval:
127.300774171 131.361729528

上图显示了基于 5000 次重复的自举过程,孕期天数 300 的预测出生体重的自举经验直方图。经验分布大致是正泰的。
我们已经通过预测的“中间 95%”,即预测的第 2.5 百分位数到第 97.5 百分位数的区间,构建了分数的约 95% 的预测区间。 区间范围从大约 127 到大约 131。基于原始样本的预测是大约 129,接近区间的中心。
改变预测变量的值的效果
下图显示了孕期天数 285 的 5,000 次自举预测的直方图。 基于原始样本的预测是约 122 盎司,区间范围从约 121 盎司到约 123 盎司。
bootstrap_prediction(baby, 'Gestational Days', 'Birth Weight', 285, 5000)
Height of regression line at x=285: 122.214571016
Approximate 95%-confidence interval:
121.177089926 123.291373304

请注意,这个区间比孕妇天数 300 的预测区间更窄。 让我们来调查其原因。
孕妇天数均值约为 279 天:
np.mean(baby.column('Gestational Days'))
279.10136286201021
所以 285 比 300 更接近分布的中心。 通常,基于自举样本的回归线,在预测变量的分布中心附近彼此更接近。 因此,所有的预测值也更接近。 这解释了预测区间的宽度更窄。
你可以在下面的图中看到这一点,它显示了 10 个自举复制品中每一个的x = 285和x = 300的预测值。 通常情况下,直线在x = 300处比x = 285处相距更远,因此x = 300的预测更加可变。
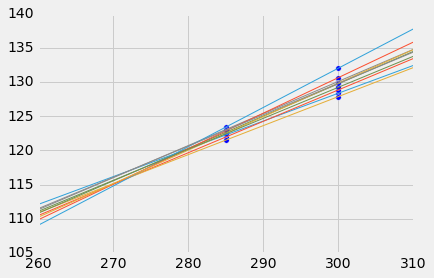
注意事项
我们在本章中进行的所有预测和测试,都假设回归模型是成立的。 具体来说,这些方法假设,散点图中的点由直线上的点产生,然后通过添加随机正态噪声将它们推离直线。
如果散点图看起来不像那样,那么模型可能不适用于数据。 如果模型不成立,那么假设模型为真的计算是无效的。
因此,在开始基于模型进行预测,或者对模型参数进行假设检验之前,我们首先要确定回归模型是否适用于我们的数据。 一个简单的方法就是,按照我们在本节所做的操作,即绘制两个变量的散点图,看看它看起来是否大致线性,并均匀分布在一条线上。 我们还应该使用残差图,执行我们在前一节中开发的诊断。