Javascript 轻量级函数式编程
第 9 章:递归
在下一页,我们将进入到递归的论题。
(本页剩余部分故意留白)
我们来谈谈递归吧。在我们入坑之前,请查阅上一页的正式定义。
我知道,这个笑话弱爆了 :)
大部分的开发人员都承认递归是一门非常强大的编程技术,但他们并不喜欢去使用它。在这个意义上,我把它放在与正则表达式相同的类别中。递归技术强大但又令人困惑,因此被视为 不值得我们投入努力。
我是递归编程的超级粉丝,你,也可以的!在这一章节中我的目标就是说服你:递归是一个重要的工具,你应该将它用在你的函数式编程中。当你正确使用时,递归编程可以轻松地描述复杂问题。
定义
所谓递归,是当一个函数调用自身,并且该调用做了同样的事情,这个循环持续到基本条件满足时,调用循环返回。
警告: 如果你不能确保基本条件是递归的 终结者,递归将会一直执行下去,并且会把你的项目损坏或锁死;恰当的基本条件十分重要!
但是... 这个定义的书面形式太让人疑惑了。我们可以做的更好些。思考下这个递归函数:
function foo(x) {
if (x < 5) return x;
return foo( x / 2 );
}
设想一下,如果我们调用 foo(16) 将会发生什么:

在 step 2 中, x / 2 的结果是 8, 这个结果以参数的形式传递到 foo(..) 并运行。同样的,在 step 3 中, x / 2 的结果是 4,这个结果以参数的形式传递到另一个 foo(..) 并运行。但愿我解释得足够直白。
但是一些人经常会在 step 4 中卡壳。一旦我们满足了基本条件 x (值为4) < 5,我们将不再调用递归函数,只是(有效地)执行了 return 4。
特别是图中返回 4 的虚线那块,它简化了那里的过程,因此我们来深入了解最后一步,并把它折分为三个子步骤:

该次的返回值会回过头来触发调用栈中所有的函数调用(并且它们都执行 return)。
另外一个递归实例:
function isPrime(num,divisor = 2){
if (num < 2 || (num > 2 && num % divisor == 0)) {
return false;
}
if (divisor <= Math.sqrt( num )) {
return isPrime( num, divisor + 1 );
}
return true;
}
这个质数的判断主要是通过验证,从2到 num 的平方根之间的每个整数,看是否存在某一整数可以整除 num (% 求余结果为 0)。如果存在这样的整数,那么 num 不是质数。反之,是质数。divisor + 1 使用递归来遍历每个可能的 divisor 值。
递归的最著名的例子之一是计算斐波那契数,该数列定义如下:
fib( 0 ): 0
fib( 1 ): 1
fib( n ):
fib( n - 2 ) + fib( n - 1 )
注意: 数列的前几个数值是: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... 每一个数字都是数列中前两个数字之和。
直接用代码来定义斐波那契:
function fib(n) {
if (n <= 1) return n;
return fib( n - 2 ) + fib( n - 1 );
}
函数 fib(..) 对自身进行了两次递归调用,这通常叫作二分递归查找。后面我们将会更多地讨论二分递归查找。
在整个章节中,我们将会用不同形式的 fib(..) 来说明关于递归的想法,但不太好的地方就是,这种特殊的方式会造成很多重复性的工作。 fib(n-1) 和 fib(n-2) 运行时候两者之间并没有任何的共享,但做的事情几乎又完全相同,这种情况一直持续到整个整数空间(译者注:形参 n)降到 0 。
在第五章的性能优化方面我们简单的谈到了记忆存储技术。本章中,记忆存储技术使得任意一个传入到 fib(..) 的数值只会被计算一次而不是多次。虽然我们不会在这里过多地讨论这个技术话题,但不论是递归或其它任何算法,我们都要谨记,性能优化是非常重要的。
相互递归
当一个函数调用自身时,很明显,这叫作直接递归。比如前面部分我们谈到的 foo(..),isPrime(..)以及 fib(..)。如果在一个递归循环中,出现两个及以上的函数相互调用,则称之为相互递归。
这两个函数就是相互递归:
function isOdd(v) {
if (v === 0) return false;
return isEven( Math.abs( v ) - 1 );
}
function isEven(v) {
if (v === 0) return true;
return isOdd( Math.abs( v ) - 1 );
}
是的,这个奇偶数的判断笨笨的。但也给我们提供了一些思路:某些算法可以根据相互递归来定义。
回顾下上节中的二分递归法 fib(..);我们可以换成相互递归来表示:
function fib_(n) {
if (n == 1) return 1;
else return fib( n - 2 );
}
function fib(n) {
if (n == 0) return 0;
else return fib( n - 1 ) + fib_( n );
}
注意: fib(..) 相互递归的实现方式改编自 “用相互递归来实现斐波纳契数列” 研究报告(https://www.researchgate.net/publication/246180510_Fibonacci_Numbers_Using_Mutual_Recursion) 。
虽然这些相互递归的示例有点不切实际,但是在更复杂的使用场景下,相互递归是非常有用的。
为什么选择递归?
现在我们已经给出了递归的定义和说明,下面来看下,为什么说递归是有用的。
递归深谙函数式编程之精髓,最被广泛引证的原因是,在调用栈中,递归把(大部分)显式状态跟踪换为了隐式状态。通常,当问题需要条件分支和回溯计算时,递归非常有用,此外在纯迭代环境中管理这种状态,是相当棘手的;最起码,这些代码是不可或缺且晦涩难懂。但是在堆栈上调用每一级的分支作为其自己的作用域,很明显,这通常会影响到代码的可读性。
简单的迭代算法可以用递归来表达:
function sum(total,...nums) {
for (let i = 0; i < nums.length; i++) {
total = total + nums[i];
}
return total;
}
// vs
function sum(num1,...nums) {
if (nums.length == 0) return num1;
return num1 + sum( ...nums );
}
我们不仅用调用栈代替了 for 循环,而且用 returns 的形式在回调栈中隐式地跟踪增量的求和( total 的间歇状态),而非在每次迭代中重新分配 total。通常,FPer 倾向于尽可能地避免重新分配局部变量。
像我们总结的那样,在基本算法里,这些差异是微乎其微的。但是,随着算法复杂度的提升,你将更加能体会到递归带来的收益,而不是这些命令式状态跟踪。
声明式递归
数学家使用 Σ 符号来表示一列数字的总和。主要原因是,如果他们使用更复杂的公式而且不得不手动书写求和的话,会造成更多麻烦(而且会降低阅读性!),比如
1 + 3 + 5 + 7 + 9 + ..。符号是数学的声明式语言!
正如 Σ 是为运算而声明,递归是为算法而声明。递归说明:一个问题存在解决方案,但并不一定要求阅读代码的人了解该解决方案的工作原理。我们来思考下找出入参最大偶数值的两种方法:
function maxEven(...nums) {
var num = -Infinity;
for (let i = 0; i < nums.length; i++) {
if (nums[i] % 2 == 0 && nums[i] > num) {
num = nums[i];
}
}
if (num !== -Infinity) {
return num;
}
}
这种实现方式不是特别难处理,但它的一些细微的问题也不容忽视。很明显,运行 maxEven(),maxEven(1) 和 maxEven(1,13) 都将会返回 undefined?最终的 if 语句是必需的吗?
我们试着换一个递归的方法来对比下。我们用下面的符号来表示递归:
maxEven( nums ):
maxEven( nums.0, maxEven( ...nums.1 ) )
换句话说,我们可以将数字列表的 max-even 定义为其余数字的 max-even 与第一个数字的 max-even 的结果。例如:
maxEven( 1, 10, 3, 2 ):
maxEven( 1, maxEven( 10, maxEven( 3, maxEven( 2 ) ) )
在 JS 中实现这个递归定义的方法之一是:
function maxEven(num1,...restNums) {
var maxRest = restNums.length > 0 ?
maxEven( ...restNums ) :
undefined;
return (num1 % 2 != 0 || num1 < maxRest) ?
maxRest :
num1;
}
那么这个方法有什么优点吗?
首先,参数与之前不一样了。我专门把第一个参数叫作 num1,剩余的其它参数放在一起叫作 restNums。我们本可以把所有参数都放在 nums 数组中,并从 nums[0] 获取第一个参数。这是为什么呢?
函数的参数是专门为递归定义的。它看起来像这样:
maxEven( num1, ...restNums ):
maxEven( num1, maxEven( ...restNums ) )
你有发现参数和递归之间的相似性吗?
当我们在函数体签名中进一步提升递归的定义,函数的声明也会得到提升。如果我们能够把递归的定义从参数反映到函数体中,那就更棒了。
但我想说最明显的改进是,for 循环造成的错乱感没有了。所有循环逻辑都被抽象为递归回调栈,所以这些东西不会造成代码混乱。我们可以轻松的把精力集中在一次比较两个数字来找到最大偶数值的逻辑中 —— 不管怎么说,这都是很重要的部分!
从思想上来讲,这如同一位数学家在更庞大的方程中使用 Σ 求和一样。我们说,“数列中剩余值的最大偶数是通过 maxEven(...restNums) 计算出来的,所以我们只需要继续推断这一部分。”
另外,我们用 restNums.length > 0 保证推断更加合理,因为当没有参数的情况下,返回的 maxRest 结果肯定是 undefined。我们不需要对这部分的推理投入额外的精力。这个基本条件(没有参数情况下)显而易见。
接下来,我们把精力放在对比 num1 和 maxRest 上 —— 算法的主要逻辑是如何确定两个数字中的哪一个(如果有的话)是最大偶数。如果 num1 不是偶数(num1 % 2 != 0),或着它小于 maxRest,那么,即使 maxRest 的值是 undefined,maxRest 会 return 掉。否则,返回结果会是 num1。
在阅读整个实现过程中,与命令式的方法相比,我所做这个例子的推理过程更加直接,核心点更加突出,少做无用功;比 for 循环中引用 无穷数值 这一方法 更具有声明性。
小贴士: 我们应该指出,除了手动迭代或递归之外,另一种(可能更好的)建模的方法是我们在在第7章中讨论的列表操作。我们先把数列中的偶数用 filter(..) 过滤出来,然后通过递归 reduce(..) 函数(对比两个数值并返回其中较大的数值)来找到最大值。在这里,我们只是使用这个例子来说明在手动迭代中递归的声明性更强。
还有一个递归的例子:计算二叉树的深度。二叉树的深度是指通过树的节点向下(左或右)的最长路径。还有另一种通过递归来定义的方式:任何树节点的深度为1(当前节点)加上来自其左侧或右侧子树的深度的最大值:
depth( node ):
1 + max( depth( node.left ), depth( node.right ) )
直接转换为二分法递归函数:
function depth(node) {
if (node) {
let depthLeft = depth( node.left );
let depthRight = depth( node.right );
return 1 + max( depthLeft, depthRight );
}
return 0;
}
我不打算列出这个算法的命令式形式,但请相信我,它太麻烦、过于命令式了。这种递归方法很不错,声明也很优雅。它遵循递归的定义,与递归定义的算法非常接近,省心。
并不是所有的问题都是完全可递归的。它不是你可以广泛应用的灵丹妙药。但是递归可以非常有效地将问题的表达,从更具必要性转变为更有声明性。
栈、堆
一起看下之前的两个递归函数 isOdd(..) 和 isEven(..):
function isOdd(v) {
if (v === 0) return false;
return isEven( Math.abs( v ) - 1 );
}
function isEven(v) {
if (v === 0) return true;
return isOdd( Math.abs( v ) - 1 );
}
如果你执行下面这行代码,在大多数浏览器里面都会报错:
isOdd( 33333 ); // RangeError: Maximum call stack size exceeded
这个错误是什么情况?引擎抛出这个错误,是因为它试图保护系统内存不会被你的程序耗尽。为了解释这个问题,我们需要先看看当函数调用时JS引擎中发生了什么。
每个函数调用都将开辟出一小块称为堆栈帧的内存。堆栈帧中包含了函数语句当前状态的某些重要信息,包括任意变量的值。之所以这样,是因为一个函数暂停去执行另外一个函数,而另外一个函数运行结束后,引擎需要返回到之前暂停时候的状态继续执行。
当第二个函数开始执行,堆栈帧增加到 2 个。如果第二个函数又调用了另外一个函数,堆栈帧将增加到 3 个,以此类推。“栈”的意思是,函数被它前一个函数调用时,这个函数帧会被“推”到最顶部。当这个函数调用结束后,它的帧会从堆栈中退出。
看下这段程序:
function foo() {
var z = "foo!";
}
function bar() {
var y = "bar!";
foo();
}
function baz() {
var x = "baz!";
bar();
}
baz();
来一步步想象下这个程序的堆栈帧:
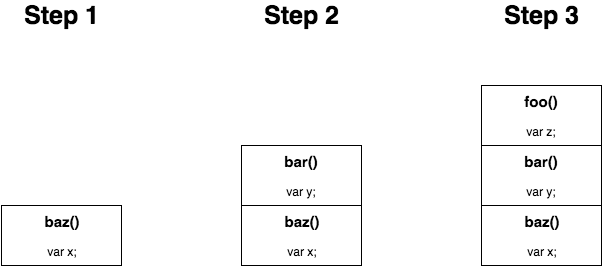
注意: 如果这些函数间没有相互调用,而只是依次执行 -- 比如前一个函数运行结束后才开始调用下一个函数 baz(); bar(); foo(); -- 则堆栈帧并没有产生;因为在下一个函数开始之前,上一个函数运行结束并把它的帧从堆栈里面移除了。
所以,每一个函数运行时候,都会占用一些内存。对多数程序来说,这没什么大不了的,不是吗?但是,一旦你引用了递归,问题就不一样了。 虽然你几乎肯定不会在一个调用栈中手动调用成千(或数百)次不同的函数,但你很容易看到产生数万个或更多递归调用的堆栈。
当引擎认为调用栈增加的太多并且应该停止增加时候,它会以主观的限制来阻止当前步骤,所以 isOdd(..) 或 isEven(..) 函数抛出了 RangeError 未知错误。这不太可能是内存接近零时候产生的限制,而是引擎的预测,因为如果这种程序持续运行下去,内存会爆掉的。由于引擎无法判断一个程序最终是否会停止,所以它必须做出确定的猜测。
引擎的限制因情况而定。规范里面并没有任何说明,因此,它也不是 必需的。但如果没有限制的话,设备很容易遭到破坏或恶意代码攻击,故而几乎所有的JS引擎都有一个限制。不同的设备环境、不同的引擎,会有不同的限制,也就无法预测或保证函数调用栈能调用多少次。
在处理大数据量时候,这个限制对于开发人员来说,会对递归的性能有一定的要求。我认为,这种限制也可能是造成开发人员不喜欢使用递归编程的最大原因。 遗憾的是,递归编程是一种编程思想而不是主流的编程技术。
尾调用
递归编程和内存限制都要比 JS 技术出现的早。追溯到上世纪 60 年代,当时开发人员想使用递归编程并希望运行在他们强大的计算机的设备,而所谓强大计算机的内存,尚远不如我们今天在手表上的内存。
幸运的是,在那个希望的原野上,进行了一个有力的观测。该技术称为 尾调用。
它的思路是如果一个回调从函数 baz() 转到函数 bar() 时候,而回调是在函数 baz() 的最底部执行 -- 也就是尾调用 -- 那么 baz() 的堆栈帧就不再需要了。也就意谓着,内存可以被回收,或只需简单的执行 bar() 函数。 如图所示:
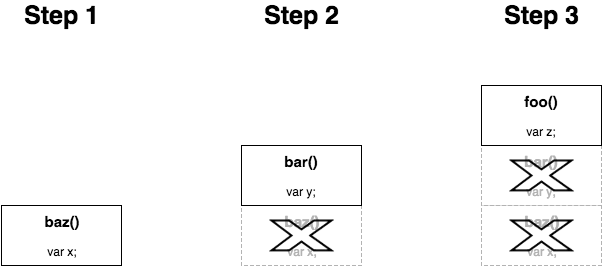
尾调用并不是递归特有的;它适用于任何函数调用。但是,在大多数情况下,你的手动非递归调用栈不太可能超过 10 级,因此尾调用对你程序内存的影响可能相当低。
在递归的情况下,尾调用作用很明显,因为这意味着递归堆栈可以“永远”运行下去,唯一的性能问题就是计算,而不再是固定的内存限制。在固定的内存中尾递归可以运行 O(1) (常数阶时间复杂度计算)。
这些技术通常被称为尾调用优化(TCO),但重点在于从优化技术中,区分出在固定内存空间中检测尾调用运行的能力。从技术上讲,尾调用并不像大多数人所想的那样,它们的运行速度可能比普通回调还慢。TCO 是关于把尾调用更加高效运行的一些优化技术。
正确的尾调用 (PTC)
在 ES6 出来之前,JavaScript 对尾调用一直没明确规定(也没有禁用)。ES6 明确规定了 PTC 的特定形式,在 ES6 中,只要使用尾调用,就不会发生栈溢出。实际上这也就意味着,只要正确的使用 PTC,就不会抛出 RangeError 这样的异常错误。
首先,在 JavaScript 中应用 PTC,必须以严格模式书写代码。如果你以前没有用过严格模式,你得试着用用了。那么,您,应该已经在使用严格模式了吧!?
其次,正确 的尾调用就像这个样子:
return foo( .. );
换句话说,函数调用应该放在最后一步去执行,并且不管返回什么东东,都得有返回( return )。这样的话,JS 就不再需要当前的堆栈帧了。
下面这些 不能 称之为 PTC:
foo();
return;
// 或
var x = foo( .. );
return x;
// 或
return 1 + foo( .. );
注意: 一些 JS 引擎 能够 把 var x = foo(); return x; 自动识别为 return foo();,这样也可以达到 PTC 的效果。但这毕竟不符合规范。
foo(..) 运行结束之后 1+ 这部分才开始执行,所以此时的堆栈帧依然存在。
不过,下面这个 是 PTC:
return x ? foo( .. ) : bar( .. );
x 进行条件判断之后,或执行 foo(..),或执行 bar(..),不论执行哪个,返回结果都会被 return 返回掉。这个例子符合 PTC 规范。
为了避免堆栈增加,PTC 要求所有的递归必须是在尾部调用,因此,二分法递归 —— 两次(或以上)递归调用 —— 是不能实现 PTC 的。我们曾在文章的前面部分展示过把二分法递归转变为相互递归的例子。也许我们可以试着化整为零,把多重递归拆分成符合 PTC 规范的单个函数回调。
重构递归
如果你想用递归来处理问题,却又超出了 JS 引擎的内存堆栈,这时候就需要重构下你的递归调用,使它能够符合 PTC 规范(或着避免嵌套调用)。这里有一些重构方法也许可以用到,但需要根据实际情况权衡。
可读性强的代码,是我们的终级目标 —— 谨记,谨记。如果使用递归后会造成代码难以阅读/理解,那就 不要使用递归;换个容易理解的方法吧。
更换堆栈
对递归来说,最主要的问题是它的内存使用情况。保持堆栈帧跟踪函数调用的状态,并将其分派给下一个递归调用迭。如果我们弄清楚了如何重新排列我们的递归,就可以用 PTC 实现递归,并利用 JS 引擎对尾调用的优化处理,那么我们就不用在内存中保留当前的堆栈帧了。
来回顾下之前用到的一个求和的例子:
function sum(num1,...nums) {
if (nums.length == 0) return num1;
return num1 + sum( ...nums );
}
这个例子并不符合 PTC 规范。sum(...nums) 运行结束之后,num1 与 sum(...nums) 的运行结果进行了累加。这样的话,当其余参数 ...nums 再次进行递归调用时候,为了得到其与 num1 累加的结果,必须要保留上一次递归调用的堆栈帧。
重构策略的关键点在于,我们可以通过把 置后 处理累加改为 提前 处理,来消除对堆栈的依赖,然后将该部分结果作为参数传递到递归调用。换句话说,我们不用在当前运用函数的堆栈帧中保留 num1 + sum(...num1) 的总和,而是把它传递到下一个递归的堆栈帧中,这样就能释放当前递归的堆栈帧。
开始之前,我们做些改动:把部分结果作为一个新的第一个参数传入到函数 sum(..):
function sum(result,num1,...nums) {
// ..
}
这次我们先把 result 和 num1 提前计算,然后把 result 作为参数一起传入:
"use strict";
function sum(result,num1,...nums) {
result = result + num1;
if (nums.length == 0) return result;
return sum( result, ...nums );
}
现在 sum(..) 已经符合 PTC 优化规范了!耶!
但是还有一个缺点,我们修改了函数的参数传递形式后,用法就跟以前不一样了。调用者不得不在需要求和的那些参数的前面,再传递一个 0 作为第一个参数。
sum( /*initialResult=*/0, 3, 1, 17, 94, 8 ); // 123
这就尴尬了。
通常,大家的处理方式是,把这个尴尬的递归函数重新命名,然后定义一个接口函数把问题隐藏起来:
"use strict";
function sumRec(result,num1,...nums) {
result = result + num1;
if (nums.length == 0) return result;
return sumRec( result, ...nums );
}
function sum(...nums) {
return sumRec( /*initialResult=*/0, ...nums );
}
sum( 3, 1, 17, 94, 8 ); // 123
情况好了些。但依然有问题:之前只需要一个函数就能解决的事,现在我们用了两个。有时候你会发现,在处理这类问题上,有些开发者用内部函数把递归 “藏了起来”:
"use strict";
function sum(...nums) {
return sumRec( /*initialResult=*/0, ...nums );
function sumRec(result,num1,...nums) {
result = result + num1;
if (nums.length == 0) return result;
return sumRec( result, ...nums );
}
}
sum( 3, 1, 17, 94, 8 ); // 123
这个方法的缺点是,每次调用外部函数 sum(..),我们都得重新创建内部函数 sumRec(..)。我们可以把他们平级放置在立即执行的函数中,只暴露出我们想要的那个的函数:
"use strict";
var sum = (function IIFE(){
return function sum(...nums) {
return sumRec( /*initialResult=*/0, ...nums );
}
function sumRec(result,num1,...nums) {
result = result + num1;
if (nums.length == 0) return result;
return sumRec( result, ...nums );
}
})();
sum( 3, 1, 17, 94, 8 ); // 123
好啦,现在即符合了 PTC 规范,又保证了 sum(..) 参数的整洁性,调用者不需要了解函数的内部实现细节。完美!
可是...天呐,本来是简单的递归函数,现在却出现了很多噪点。可读性已经明显降低。至少说,这是不成功的。有些时候,这只是我们能做的最好的。
幸运的事,在一些其它的例子中,比如上一个例子,有一个比较好的方式。一起重新看下:
"use strict";
function sum(result,num1,...nums) {
result = result + num1;
if (nums.length == 0) return result;
return sum( result, ...nums );
}
sum( /*initialResult=*/0, 3, 1, 17, 94, 8 ); // 123
也许你会注意到,result 就像 num1 一样,也就是说,我们可以把列表中的第一个数字作为我们的运行总和;这甚至包括了第一次调用的情况。我们需要的是重新命名这些参数,使函数清晰可读:
"use strict";
function sum(num1,num2,...nums) {
num1 = num1 + num2;
if (nums.length == 0) return num1;
return sum( num1, ...nums );
}
sum( 3, 1, 17, 94, 8 ); // 123
帅呆了。比之前好了很多,嗯?!我认为这种模式在声明/合理和执行之间达到了很好的平衡。
让我们试着重构下前面的 maxEven(..)(目前还不符合 PTC 规范)。就像之前我们把参数的和作为第一个参数一样,我们可以依次减少列表中的数字,同时一直把遇到的最大偶数作为第一个参数。
为了清楚起见,我们可能使用算法策略(类似于我们之前讨论过的):
- 首先对前两个参数
num1和num2进行对比。 - 如果
num1是偶数,并且num1大于num2,num1保持不变。 - 如果
num2是偶数,把num2赋值给num1。 - 否则的话,
num1等于undefined。 - 如果除了这两个参数之外,还存在其它参数
nums,把它们与num1进行递归对比。 - 最后,不管是什么值,只需返回
num1。
依照上面的步骤,代码如下:
"use strict";
function maxEven(num1,num2,...nums) {
num1 =
(num1 % 2 == 0 && !(maxEven( num2 ) > num1)) ?
num1 :
(num2 % 2 == 0 ? num2 : undefined);
return nums.length == 0 ?
num1 :
maxEven( num1, ...nums )
}
注意: 函数第一次调用 maxEven(..) 并不是为了 PTC 优化,当它只传递 num2 时,只递归一级就返回了;它只是一个避免重复 % 逻辑的技巧。因此,只要该调用是完全不同的函数,就不会增加递归堆栈。第二次调用 maxEven(..) 是基于 PTC 优化角度的真正递归调用,因此不会随着递归的进行而造成堆栈的增加。
重申下,此示例仅用于说明将递归转化为符合 PTC 规范以优化堆栈(内存)使用的方法。求最大偶数值的更直接方法可能是,先对参数列表中的 nums 过滤,然后冒泡或排序处理。
基于 PTC 重构递归,固然对简单的声明形式有一些影响,但依然有理由去做这样的事。不幸的是,存在一些递归,即使我们使用了接口函数来扩展,也不会很好,因此,我们需要有不同的思路。
后继传递格式 (CPS)
在 JavaScript 中, continuation 一词通常用于表示在某个函数完成后指定需要执行的下一个步骤的回调函数。组织代码,使得每个函数在其结束时接收另一个执行函数,被称为后继传递格式(CPS)。
有些形式的递归,实际上是无法按照纯粹的 PTC 规范重构的,特别是相互递归。我们之前提到过的 fib(..) 函数,以及我们派生出来的相互递归形式。这两个情况,皆是存在多个递归调用,这些递归调用阻碍了 PTC 内存优化。
但是,你可以执行第一个递归调用,并将后续递归调用包含在后续函数中并传递到第一个调用。尽管这意味着最终需要在堆栈中执行更多的函数,但由于后继函数所包含的都是 PTC 形式的,所以堆栈内存的使用情况不会无限增长。
把 fib(..) 做如下修改:
"use strict";
function fib(n,cont = identity) {
if (n <= 1) return cont( n );
return fib(
n - 2,
n2 => fib(
n - 1,
n1 => cont( n2 + n1 )
)
);
}
仔细看下都做了哪些事情。首先,我们默认用了第三章中的 cont(..) 后继函数表示 identity(..);记住,它只简单的返回传递给它的任何东西。
更重要的是,这里面增加了不仅仅是一个而是两个后续函数。第一个后续函数接收 fib(n-2) 的运行结果作为参数 n2。第二个内部后续函数接收 fib(n-1)的运行结果作为参数 n1。当得到 n1 和 n2 的值后,两者再相加 (n2 + n1),相加的运行结果会传入到下一个后续函数 cont(..)。
也许这将有助于我们梳理下流程:就像我们之前讨论的,在递归堆栈之后,当我们传递部分结果而不是返回它们时,每一步都被包含在一个后续函数中,这拖慢了计算速度。这个技巧允许我们执行多个符合 PTC 规范的步骤。
在静态语言中,CPS通常为尾调用提供了编译器可以自动识别并重新排列递归代码以利用的机会。很可惜,不能用在原生 JS 上。
在 JavaScript 中,你得自己书写出符合 CPS 格式的代码。这并不是明智的做法;以命令符号声明的形式肯定会让内容有些不清楚。 但总的来说,这种形式仍然要比 for 循环更具有声明性。
警告: 我们需要注意的一个比较重要的事项是,在 CPS 中,创建额外的内部后续函数仍然消耗内存,但有些不同。并不是之前的堆栈帧累积,闭包只是消耗多余的内存空间(一般情况下,是堆栈里面的多余内存空间)。在这些情况下,引擎似乎没有启动 RangeError 限制,但这并不意味着你的内存使用量是按比例固定好的。
弹簧床
除了 CPS 后续传递格式之外,另外一种内存优化的技术称为弹簧床。在弹簧床格式的代码中,同样的创建了类似 CPS 的后续函数,不同的是,它们没有被传递,而是被简单的返回了。
不再是函数调用另外的函数,堆栈的深度也不会大于一层,因为每个函数只会返回下一个将调用的函数。循环只是继续运行每个返回的函数,直到再也没有函数可运行。
弹簧床的优点之一是在非 PTC 环境下你一样可以应用此技术。另一个优点是每个函数都是正常调用,而不是 PTC 优化,所以它可以运行得更快。
一起来试下 trampoline(..):
function trampoline(fn) {
return function trampolined(...args) {
var result = fn( ...args );
while (typeof result == "function") {
result = result();
}
return result;
};
}
当返回一个函数时,循环继续,执行该函数并返回其运行结果,然后检查返回结果的类型。一旦返回的结果类型不是函数,弹簧床就认为函数调用完成了并返回结果值。
所以我们可能需要使用前面讲到的,将部分结果作为参数传递的技巧。以下是我们在之前的数组求和中使用此技巧的示例:
var sum = trampoline(
function sum(num1,num2,...nums) {
num1 = num1 + num2;
if (nums.length == 0) return num1;
return () => sum( num1, ...nums );
}
);
var xs = [];
for (let i=0; i<20000; i++) {
xs.push( i );
}
sum( ...xs ); // 199990000
缺点是你需要将递归函数包裹在执行弹簧床功能的函数中; 此外,就像 CPS 一样,需要为每个后续函数创建闭包。然而,与 CPS 不一样的地方是,每个返回的后续数数,运行并立即完成,所以,当调用堆栈的深度用尽时,引擎中不会累积越来越多的闭包。
除了执行和记忆性能之外,弹簧床技术优于CPS的优点是它们在声明递归形式上的侵入性更小,由于你不必为了接收后续函数的参数而更改函数参数,所以除了执行和内存性能之外,弹簧床技术优于 CPS 的地方还有,它们在声明递归形式上侵入性更小。虽然弹簧床技术并不是理想的,但它们可以有效地在命令循环代码和声明性递归之间达到平衡。
总结
递归,是指函数递归调用自身。呃,这就是递归的定义。明白了吧!?
直递归是指对自身至少调用一次,直到满足基本条件才能停止调用。多重递归(像二分递归)是指对自身进行多次调用。相互递归是当两个或以上函数循环递归 相互 调用。而递归的优点是它更具声明性,因此通常更易于阅读。
递归的优点是它更具声明性,因此通常更易于阅读。缺点通常是性能方面,但是相比执行速度,更多的限制在于内存方面。
尾调用是通过减少或释放堆栈帧来节约内存空间。要在 JavaScript 中实现尾调用 “优化”,需要基于严格模式和适当的尾调用( PTC )。我们也可以混合几种技术来将非 PTC 递归函数重构为 PTC 格式,或者至少能通过平铺堆栈来节约内存空间。
谨记:递归应该使代码更容易读懂。如果你误用或滥用递归,代码的可读性将会比命令形式更糟。千万不要这样做。