第二章:推荐系统入门
原文:http://guidetodatamining.com/chapter-2/
内容:
- 推荐系统工作原理
- 社会化协同过滤工作原理
- 如何找到相似物品
- 曼哈顿距离
- 欧几里得距离
- 闵可夫斯基距离
- 皮尔逊相关系数
- 余弦相似度
- 使用Python实现K最邻近算法
- 图书漂流站(BookCrossing)数据集
你喜欢的东西我也喜欢
我们将从推荐系统开始,开启数据挖掘之旅。推荐系统无处不在,如亚马逊网站的“看过这件商品的顾客还购买过”板块:

last.fm上对音乐和演唱会的推荐(相似歌手):

在亚马逊的例子里,它用了两个元素来进行推荐:一是我浏览了里维斯翻译的《法华经》一书;二是其他浏览过该书的顾客还浏览过的译作。
本章我们讲述的推荐方法称为协同过滤。顾名思义,这个方法是利用他人的喜好来进行推荐,也就是说,是大家一起产生的推荐。他的工作原理是这样的:如果要推荐一本书给你,我会在网站上查找一个和你类似的用户,然后将他喜欢的书籍推荐给你——比如巴奇加卢比的《发条女孩》。
如何找到相似的用户?
所以首先要做的工作是找到相似的用户。这里用最简单的二维模型来描述。假设用户会在网站用五颗星来评价一本书——没有星表示书写得很糟,五颗星表示很好。因为我们用的是二维模型,所以仅对两本书进行评价:史蒂芬森的《雪崩》(纵轴)和拉尔森的《龙纹身的女孩》(横轴)。
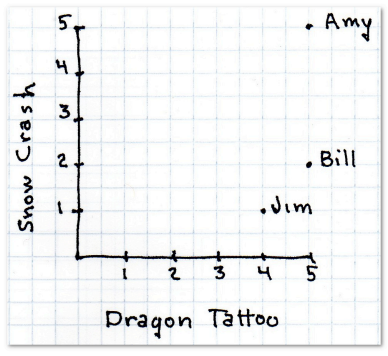
首先,下表显示有三位用户对这两本书做了评价:

现在我想为神秘的X先生推荐一本书,他给《雪崩》打了四星,《龙纹身的女孩》两星。第一个任务是找出哪个用户和他最为相似。我们用距离来表示。
曼哈顿距离
最简单的距离计算方式是曼哈顿距离。在二维模型中,每个人都可以用(x, y)的点来表示,这里我用下标来表示不同的人,(x1, y1)表示艾米,(x2, y2)表示那位神秘的X先生,那么他们之间的曼哈顿距离就是:
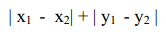
也就是x之差的绝对值加上y之差的绝对值,这样他们的距离就是4。
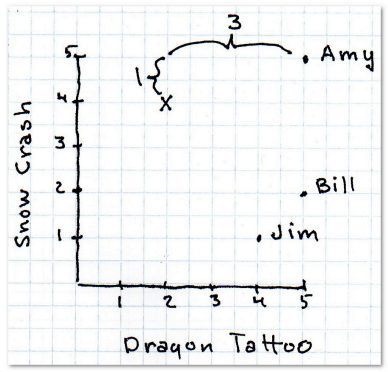
完整的计算结果如下:

艾米的距离最近,在她的浏览历史中可以看到她曾给巴奇加卢比的《发条女孩》打过五星,于是我们就可以把这本书推荐给X先生。
欧几里得距离
曼哈顿距离的优点之一是计算速度快,对于Facebook这样需要计算百万用户之间的相似度时就非常有利。
勾股定理
也许你还隐约记得勾股定理。另一种计算距离的方式就是看两点之间的直线距离:

利用勾股定理,我们可以如下计算距离:
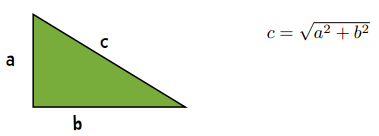
这条斜线就是欧几里得距离,公式是:

回顾一下,这里的x1表示用户1喜欢《龙纹身》的程度,x2是用户2喜欢这本书的程度;y1则是用户1喜欢《雪崩》的程度,y2是用户2喜欢这本书的程度。
艾米给《龙纹身》和《雪崩》都打了五颗星,神秘的X先生分别打了两星和四星,这样他们之间的欧几里得距离就是:
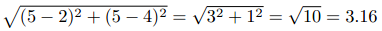
以下是全部用户的计算结果:

N维模型
刚才我们仅仅对两本书进行评价(二维模型),下面让我们扩展一下,尝试更复杂的模型。假设我们现在要为一个在线音乐网站的用户推荐乐队。用户可以用1至5星来评价一个乐队,其中包含半星(如2.5星)。下表展示了8位用户对8支乐队的评价:
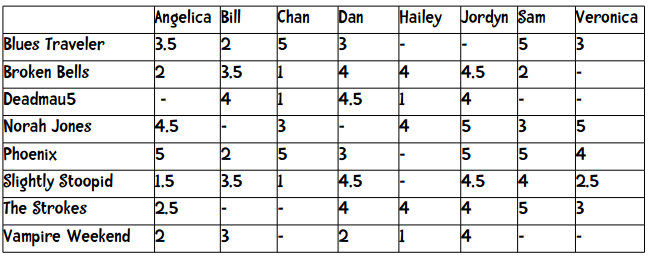
表中的短横表示这位用户没有给这支乐队打分。我们在计算两个用户的距离时,只采用他们都评价过的乐队,比如要计算Angelica和Bill的距离,我们只会用到5支乐队。这两个用户的曼哈顿距离为:
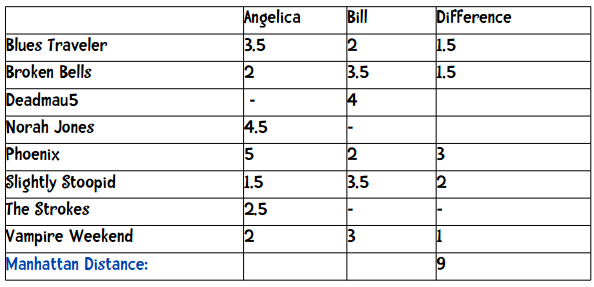
最后距离即是上方数据的加和:(1.5 + 1.5 + 3 + 2 + 1)。
计算欧几里得距离的方法也是类似的,我们也只取双方都评价过的乐队。
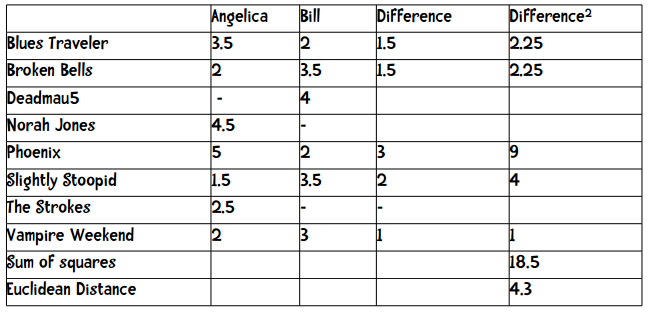
用公式来描述即:
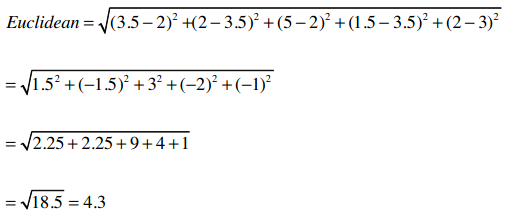
掌握了吗? 那就试试计算其他几个用户之间的距离吧。

有个瑕疵
当我们计算Hailey和Veronica的距离时会发现一个问题:他们共同评价的乐队只有两支(Norah Jones和The Strokes),而Hailey和Jordyn共同评价了五支乐队,这似乎会影响我们的计算结果,因为Hailey和Veronica之间是二维的,而Haily和Veronica之间是五维的。曼哈顿距离和欧几里得距离在数据完整的情况下效果最好。如何处理缺失数据,这在研究领域仍是一个活跃的话题。本书的后续内容会进行一些讨论,这里先不展开。现在,让我们开始构建一个推荐系统吧。
推广:闵可夫斯基距离
我们可以将曼哈顿距离和欧几里得距离归纳成一个公式,这个公式称为闵可夫斯基距离:
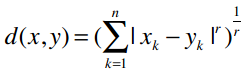
其中:
r = 1该公式即曼哈顿距离r = 2该公式即欧几里得距离r = ∞极大距离

当你在书中看到这些数学公式,你可以选择快速略过它,继续读下面的文字,过去我就是这样;你也可以停下来,好好分析一下这些公式,会发现其实它们并不难理解。比如上面的公式,当r = 1时,可以简化成如下形式:
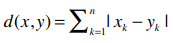
仍用上文的音乐站点为例,x和y分别表示两个用户,d(x, y)表示他们之间的距离,n表示他们共同评价过的乐队数量,我们之前已经做过计算:
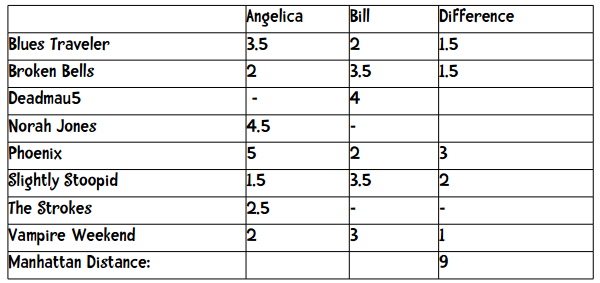
其中Difference一栏表示两者评分之差的绝对值,加起来等于9,也就是他们之间的距离。
当r = 2时,我们得到欧几里得距离的计算公式:
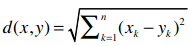
提前预告一下:r值越大,单个维度的差值大小会对整体距离有更大的影响。

使用Python代码来表示数据(终于要开始编程了)
在Python中,我们可以用多种方式来描述上表中的数据,这里我选择Python的字典类型(或者称为关联数组、哈希表)。
注:本书的所有代码可以在这里找到。
users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoenix": 5.0, "Slightly Stoopid": 1.5, "The Strokes": 2.5, "Vampire Weekend": 2.0},
"Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5, "Deadmau5": 4.0, "Phoenix": 2.0, "Slightly Stoopid": 3.5, "Vampire Weekend": 3.0},
"Chan": {"Blues Traveler": 5.0, "Broken Bells": 1.0, "Deadmau5": 1.0, "Norah Jones": 3.0, "Phoenix": 5, "Slightly Stoopid": 1.0},
"Dan": {"Blues Traveler": 3.0, "Broken Bells": 4.0, "Deadmau5": 4.5, "Phoenix": 3.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 2.0},
"Hailey": {"Broken Bells": 4.0, "Deadmau5": 1.0, "Norah Jones": 4.0, "The Strokes": 4.0, "Vampire Weekend": 1.0},
"Jordyn": {"Broken Bells": 4.5, "Deadmau5": 4.0, "Norah Jones": 5.0, "Phoenix": 5.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 4.0},
"Sam": {"Blues Traveler": 5.0, "Broken Bells": 2.0, "Norah Jones": 3.0, "Phoenix": 5.0, "Slightly Stoopid": 4.0, "The Strokes": 5.0},
"Veronica": {"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
}
我们可以用以下方式来获取某个用户的评分:
>>> users["Veronica"]
{"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
>>>
计算曼哈顿距离
def manhattan(rating1, rating2):
"""计算曼哈顿距离。rating1和rating2参数中存储的数据格式均为
{'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
distance = 0
for key in rating1:
if key in rating2:
distance += abs(rating1[key] - rating2[key])
return distance
我们可以做一下测试:
>>> manhattan(users['Hailey'], users['Veronica'])
2.0
>>> manhattan(users['Hailey'], users['Jordyn'])
7.5
>>>
下面我们编写一个函数来找出距离最近的用户(其实该函数会返回一个用户列表,按距离排序):
def computeNearestNeighbor(username, users):
"""计算所有用户至username用户的距离,倒序排列并返回结果列表"""
distances = []
for user in users:
if user != username:
distance = manhattan(users[user], users[username])
distances.append((distance, user))
# 按距离排序——距离近的排在前面
distances.sort()
return distances
简单测试一下:
>>> computeNearestNeighbor("Hailey", users)
[(2.0, 'Veronica'), (4.0, 'Chan'), (4.0, 'Sam'), (4.5, 'Dan'), (5.0, 'Angelica'), (5.5, 'Bill'), (7.5, 'Jordyn')]
最后,我们结合以上内容来进行推荐。假设我想为Hailey做推荐,这里我找到了离他距离最近的用户Veronica。然后,我会找到出Veronica评价过但Hailey没有评价的乐队,并假设Hailey对这些陌生乐队的评价会和Veronica相近。比如,Hailey没有评价过Phoenix乐队,而Veronica对这个乐队打出了4分,所以我们认为Hailey也会喜欢这支乐队。下面的函数就实现了这一逻辑:
def recommend(username, users):
"""返回推荐结果列表"""
# 找到距离最近的用户
nearest = computeNearestNeighbor(username, users)[0][1]
recommendations = []
# 找出这位用户评价过、但自己未曾评价的乐队
neighborRatings = users[nearest]
userRatings = users[username]
for artist in neighborRatings:
if not artist in userRatings:
recommendations.append((artist, neighborRatings[artist]))
# 按照评分进行排序
return sorted(recommendations, key=lambda artistTuple: artistTuple[1], reverse = True)
下面我们就可以用它来为Hailey做推荐了:
>>> recommend('Hailey', users)
[('Phoenix', 4.0), ('Blues Traveler', 3.0), ('Slightly Stoopid', 2.5)]
运行结果和我们的预期相符。我们看可以看到,和Hailey距离最近的用户是Veronica,Veronica对Phoenix乐队打了4分。我们再试试其他人:
>>> recommend('Chan', users)
[('The Strokes', 4.0), ('Vampire Weekend', 1.0)]
>>> recommend('Sam', users)
[('Deadmau5', 1.0)]
我们可以猜想Chan会喜欢The Strokes乐队,而Sam不会太欣赏Deadmau5。
>>> recommend('Angelica', users)
[]
对于Angelica,我们得到了空的返回值,也就是说我们无法对其进行推荐。让我们看看是哪里有问题:
>>> computeNearestNeighbor('Angelica', users)
[(3.5, 'Veronica'), (4.5, 'Chan'), (5.0, 'Hailey'), (8.0, 'Sam'), (9.0, 'Bill'), (9.0, 'Dan'), (9.5, 'Jordyn')]
Angelica最相似的用户是Veronica,让我们回头看看数据:

我们可以看到,Veronica评价过的乐队,Angelica也都评价过了,所以我们没有推荐。
之后,我们会讨论如何解决这一问题。
作业:实现一个计算闵可夫斯基距离的函数,并在计算用户距离时使用它。
def minkowski(rating1, rating2, r):
distance = 0
for key in rating1:
if key in rating2:
distance += pow(abs(rating1[key] - rating2[key]), r)
return pow(distance, 1.0 / r)
# 修改computeNearestNeighbor函数中的一行
distance = minkowski(users[user], users[username], 2)
# 这里2表示使用欧几里得距离
用户的问题
让我们仔细看看用户对乐队的评分,可以发现每个用户的打分标准非常不同:
- Bill没有打出极端的分数,都在2至4分之间;
- Jordyn似乎喜欢所有的乐队,打分都在4至5之间;
- Hailey是一个有趣的人,他的分数不是1就是4。
那么,如何比较这些用户呢?比如Hailey的4分相当于Jordan的4分还是5分呢?我觉得更接近5分。这样一来就会影响到推荐系统的准确性了。

- 左:我非常喜欢Broken Bells乐队,所以我给他们打4分!
- 右:Broken Bells乐队还可以,我打4分。
皮尔逊相关系数
解决方法之一是使用皮尔逊相关系数。简单起见,我们先看下面的数据(和之前的数据不同):
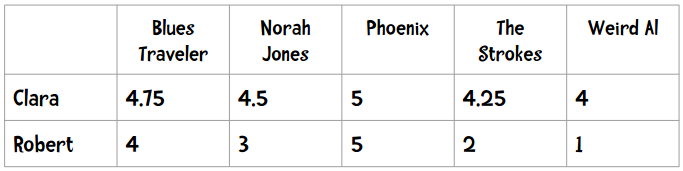
这种现象在数据挖掘领域称为“分数膨胀”。Clara最低给了4分——她所有的打分都在4至5分之间。我们将它绘制成图表:
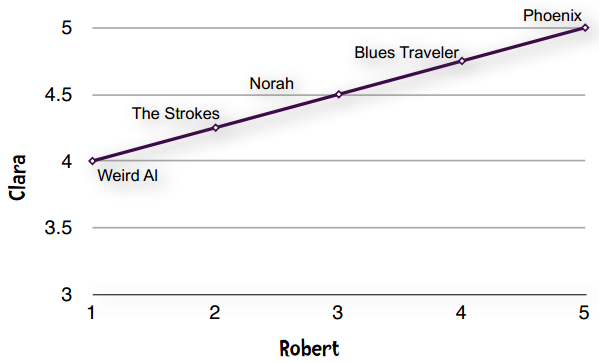
一条直线——完全吻合!!!
直线即表示Clara和Robert的偏好完全一致。他们都认为Phoenix是最好的乐队,然后是Blues Traveler、Norah Jones。如果Clara和Robert的意见不一致,那么落在直线上的点就越少。
意见基本一致的情形

意见不太一致的情形
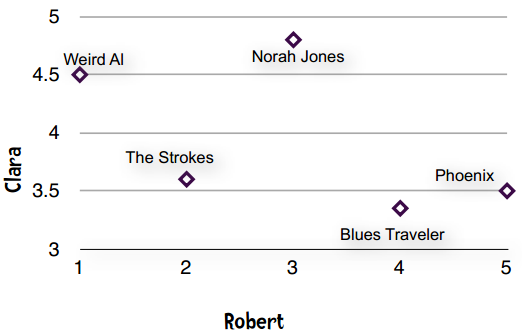
所以从图表上理解,意见相一致表现为一条直线。皮尔逊相关系数用于衡量两个变量之间的相关性(这里的两个变量指的是Clara和Robert),它的值在-1至1之间,1表示完全吻合,-1表示完全相悖。从直观上理解,最开始的那条直线皮尔逊相关系数为1,第二张是0.91,第三张是0.81。因此我们利用这一点来找到相似的用户。
皮尔逊相关系数的计算公式是:
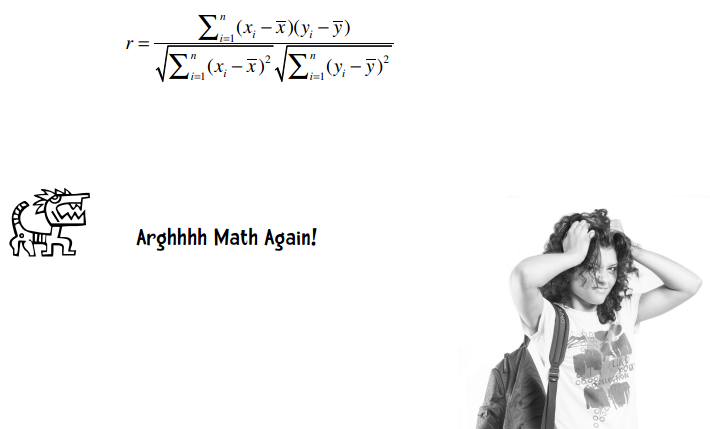
这里我说说自己的经历。我大学读的是现代音乐艺术,课程包括芭蕾、现代舞、服装设计等,没有任何数学课程。我高中读的是男子学校,学习了管道工程和汽车维修,只懂得很基础的数学知识。不知是因为我的学科背景,还是习惯于用直觉来思考,当我遇到这样的数学公式时会习惯性地跳过,继续读下面的文字。如果你和我一样,我强烈建议你与这种惰性抗争,试着去理解这些公式。它们虽然看起来很复杂,但还是能够被常人所理解的。
上面的公式除了看起来比较复杂,另一个问题是要获得计算结果必须对数据做多次遍历。好在我们有另外一个公式,能够计算皮尔逊相关系数的近似值:
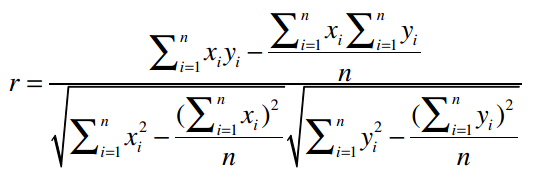
这个公式虽然看起来更加复杂,而且其计算结果会不太稳定,有一定误差存在,但它最大的优点是,用代码实现的时候可以只遍历一次数据,我们会在下文看到。首先,我们将这个公式做一个分解,计算下面这个表达式的值:
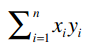
对于Clara和Robert,我们可以得到:
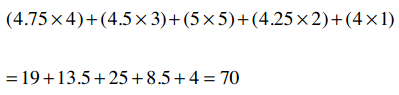
很简单把?下面我们计算这个公式:

Clara的总评分是22.5, Robert是15,他们评价了5支乐队,因此:
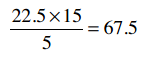
所以,那个巨型公式的分子就是70 - 67.5 = 2.5。
下面我们来看分母:
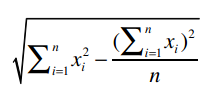
首先:

我们已经计算过Clara的总评分是22.5,它的平方是506.25,除以乐队的数量5,得到101.25。综合得到:

对于Robert,我们用同样的方法计算:
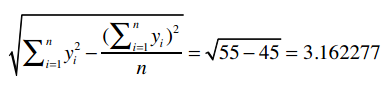
最后得到:
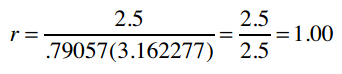
因此,1表示Clara和Robert的偏好完全吻合。
先休息一下吧

计算皮尔逊相关系数的代码
from math import sqrt
def pearson(rating1, rating2):
sum_xy = 0
sum_x = 0
sum_y = 0
sum_x2 = 0
sum_y2 = 0
n = 0
for key in rating1:
if key in rating2:
n += 1
x = rating1[key]
y = rating2[key]
sum_xy += x * y
sum_x += x
sum_y += y
sum_x2 += pow(x, 2)
sum_y2 += pow(y, 2)
# 计算分母
denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n)
if denominator == 0:
return 0
else:
return (sum_xy - (sum_x * sum_y) / n) / denominator
测试一下:
>>> pearson(users['Angelica'], users['Bill'])
-0.9040534990682699
>>> pearson(users['Angelica'], users['Hailey'])
0.42008402520840293
>>> pearson(users['Angelica'], users['Jordyn'])
0.7639748605475432
最后一个公式:余弦相似度
这里我将奉上最后一个公式:余弦相似度。它在文本挖掘中应用得较多,在协同过滤中也会使用到。为了演示如何使用该公式,我们换一个示例。这里记录了每个用户播放歌曲的次数,我们用这些数据进行推荐:
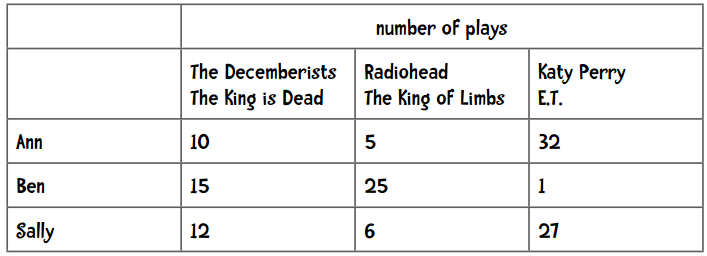
简单扫一眼上面的数据(或者用之前讲过的距离计算公式),我们可以发现Ann的偏好和Sally更为相似。
问题在哪儿?
我在iTunes上有大约4000首歌曲,下面是我最常听的音乐:
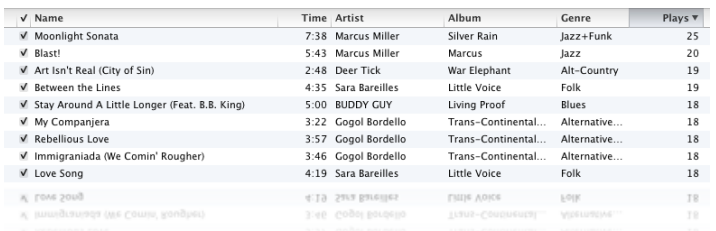
可以看到,Moonlight Sonata这首歌我播放了25次,但很有可能你一次都没有听过。事实上,上面列出的这些歌曲可能你一首都没听过。此外,iTunes上有1500万首音乐,而我只听过4000首。所以说单个用户的数据是 稀疏 的,因为非零值较总体要少得多。当我们用1500万首歌曲来比较两个用户时,很有可能他们之间没有任何交集,这样一来就无从计算他们之间的距离了。

类似的情况是在计算两篇文章的相似度时。比如说我们想找一本和《The Space Pioneers》相类似的书,方法之一是利用单词出现的频率,即统计每个单词在书中出现的次数占全书单词的比例,如“the”出现频率为6.13%,“Tom” 0.89%,“space” 0.25%。我们可以用这些数据来寻找一本相近的书。但是,这里同样有数据的稀疏性问题。《The Space Pioneers》中有6629个不同的单词,但英语语言中有超过100万个单词,这样一来非零值就很稀少了,也就不能计算两本书之间的距离。
余弦相似度的计算中会略过这些非零值。它的计算公式是:

其中,“·”号表示数量积。“||x||”表示向量x的模,计算公式是:
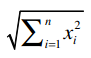
我们用上文中“偏好完全一致”的示例:

所以两个向量为:
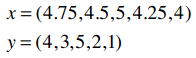
它们的模是:
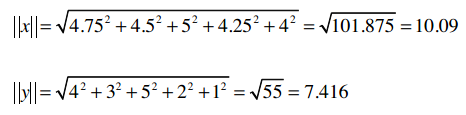
数量积的计算:

因此余弦相似度是:
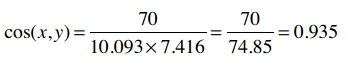
余弦相似度的范围从1到-1,1表示完全匹配,-1表示完全相悖。所以0.935表示匹配度很高。
作业:尝试计算Angelica和Veronica的余弦相似度
应该使用哪种相似度?
我们整本书都会探索这个问题,以下是一些提示:

- 如果数据存在“分数膨胀”问题,就使用皮尔逊相关系数。
- 如果数据比较“密集”,变量之间基本都存在公有值,且这些距离数据是非常重要的,那就使用欧几里得或曼哈顿距离。
- 如果数据是稀疏的,则使用余弦相似度。
所以,如果数据是密集的,曼哈顿距离和欧几里得距离都是适用的。那么稀疏的数据可以使用吗?我们来看一个也和音乐有关的示例:假设有三个人,每人都给100首音乐评过分。

- Jake(左):乡村音乐的忠实听众。
- Linda和Eric(右):我们爱六十年代的摇滚乐!
Linda和Eric喜欢相同的音乐,他们的评分列表中有20首相同的的歌曲,且评分均值相差不到0.5!所以他们之间的曼哈顿距离为20 x 0.5 = 10,欧几里得距离则为:
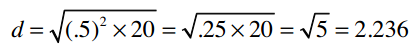
Linda和Jake只共同评分了一首歌曲:Chris Cagle的 What a Beautiful Day 。Linda打了3分,Jake打了5分,所以他们之间的曼哈顿距离为2,欧几里得距离为:
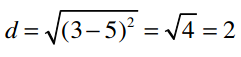
所以不管是曼哈顿距离还是欧几里得距离,Jake都要比Eric离Linda近,这不符合实际情况。

嘿,我想到一个办法。人们给音乐打分是从1到5分,那些没有打分的音乐就统一给0分好了,这样就能解决数据稀疏的问题了!
想法不错,但是这样做也不行。为了解释这一问题,我们再引入两个人到例子里来:Cooper和Kelsey。他们和Jake都有着非常相似的音乐偏好,其中Jake在我们网站上评价了25首歌曲。

Cooper评价了26首歌曲,其中25首和Jake是一样的。他们对每首歌曲的评价差值只有0.25!
Kelsey在我们网站上评价了150首歌曲,其中25首和Jake相同。和Cooper一样,她和Jake之间的评价差值也只有0.25!
所以我们从直觉上看Cooper和Keylsey离Jake的距离应该相似。但是,当我们计算他们之间的曼哈顿距离和欧几里得距离时(代入0值),会发现Cooper要比Keylsey离Jake近得多。
为什么呢?
我们来看下面的数据:
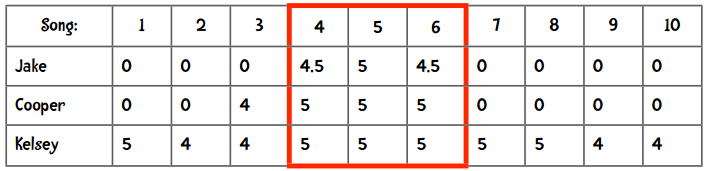
从4、5、6这三首歌来看,两人离Jake的距离是相同的,但计算出的曼哈顿距离却不这么显示:
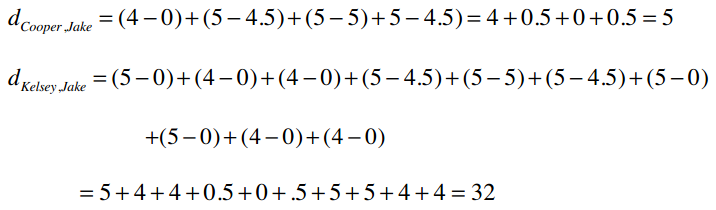
问题就在于数据中的0值对结果的影响很大,所以用0代替空值的方法并不比原来的方程好。还有一种变通的方式是计算“平均值”——将两人共同评价过的歌曲分数除以歌曲数量。
总之,曼哈顿距离和欧几里得距离在数据完整的情况下会运作得非常好,如果数据比较稀疏,则要考虑使用余弦距离。
古怪的现象
假设我们要为Amy推荐乐队,她喜欢Phoenix、Passion Pit、以及Vampire Weekend。和她最相似的用户是Bob,他也喜欢这三支乐队。他的父亲为Walter Ostanek乐队演奏手风琴,所以受此影响,他给了这支乐队5星评价。按照我们现在的推荐逻辑,我们会将这支乐队推荐给Amy,但有可能她并不喜欢。

或者试想一下,Billy Bob Olivera教授喜欢阅读数据挖掘方面的书籍以及科幻小说,他最邻近的用户是我,因为我也喜欢这两种书。然而,我又是一个贵宾犬的爱好者,所以给《贵宾犬的隐秘生活》这本书打了很高的分。这样一来,现有的推荐方法会将这本书介绍给Olivera教授。

问题就在于我们只依靠最相似的 一个 用户来做推荐,如果这个用户有些特殊的偏好,就会直接反映在推荐内容里。解决方法之一是找寻多个相似的用户,这里就要用到K最邻近算法了。
K最邻近算法
在协同过滤中可以使用K最邻近算法来找出K个最相似的用户,以此作为推荐的基础。不同的应用有不同的K值,需要做一些实验来得出。以下给到读者一个基本的思路。
假设我要为Ann做推荐,并令K=3。使用皮尔逊相关系数得到的结果是:

这三个人都会对推荐结果有所贡献,问题在于我们如何确定他们的比重呢?我们直接用相关系数的比重来描述,Sally的比重是0.8/2=40%,Eric是0.7/2=35%,Amanda则是25%:
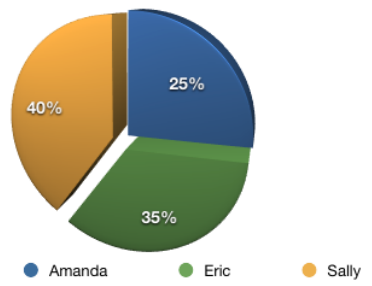
假设他们三人对Grey Wardens的评分以及加权后的结果如下:

最后计算得到的分数为:
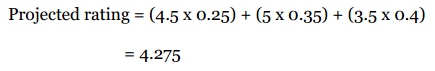
Python推荐模块
我将本章学到的内容都汇集成了一个Python类,虽然代码有些长,我还是贴在了这里:
import codecs
from math import sqrt
users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0,
"Norah Jones": 4.5, "Phoenix": 5.0,
"Slightly Stoopid": 1.5,
"The Strokes": 2.5, "Vampire Weekend": 2.0},
"Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5,
"Deadmau5": 4.0, "Phoenix": 2.0,
"Slightly Stoopid": 3.5, "Vampire Weekend": 3.0},
"Chan": {"Blues Traveler": 5.0, "Broken Bells": 1.0,
"Deadmau5": 1.0, "Norah Jones": 3.0, "Phoenix": 5,
"Slightly Stoopid": 1.0},
"Dan": {"Blues Traveler": 3.0, "Broken Bells": 4.0,
"Deadmau5": 4.5, "Phoenix": 3.0,
"Slightly Stoopid": 4.5, "The Strokes": 4.0,
"Vampire Weekend": 2.0},
"Hailey": {"Broken Bells": 4.0, "Deadmau5": 1.0,
"Norah Jones": 4.0, "The Strokes": 4.0,
"Vampire Weekend": 1.0},
"Jordyn": {"Broken Bells": 4.5, "Deadmau5": 4.0,
"Norah Jones": 5.0, "Phoenix": 5.0,
"Slightly Stoopid": 4.5, "The Strokes": 4.0,
"Vampire Weekend": 4.0},
"Sam": {"Blues Traveler": 5.0, "Broken Bells": 2.0,
"Norah Jones": 3.0, "Phoenix": 5.0,
"Slightly Stoopid": 4.0, "The Strokes": 5.0},
"Veronica": {"Blues Traveler": 3.0, "Norah Jones": 5.0,
"Phoenix": 4.0, "Slightly Stoopid": 2.5,
"The Strokes": 3.0}
}
class recommender:
def __init__(self, data, k=1, metric='pearson', n=5):
""" 初始化推荐模块
data 训练数据
k K邻近算法中的值
metric 使用何种距离计算方式
n 推荐结果的数量
"""
self.k = k
self.n = n
self.username2id = {}
self.userid2name = {}
self.productid2name = {}
# 将距离计算方式保存下来
self.metric = metric
if self.metric == 'pearson':
self.fn = self.pearson
#
# 如果data是一个字典类型,则保存下来,否则忽略
#
if type(data).__name__ == 'dict':
self.data = data
def convertProductID2name(self, id):
"""通过产品ID获取名称"""
if id in self.productid2name:
return self.productid2name[id]
else:
return id
def userRatings(self, id, n):
"""返回该用户评分最高的物品"""
print ("Ratings for " + self.userid2name[id])
ratings = self.data[id]
print(len(ratings))
ratings = list(ratings.items())
ratings = [(self.convertProductID2name(k), v)
for (k, v) in ratings]
# 排序并返回结果
ratings.sort(key=lambda artistTuple: artistTuple[1],
reverse = True)
ratings = ratings[:n]
for rating in ratings:
print("%s\t%i" % (rating[0], rating[1]))
def loadBookDB(self, path=''):
"""加载BX数据集,path是数据文件位置"""
self.data = {}
i = 0
#
# 将书籍评分数据放入self.data
#
f = codecs.open(path + "BX-Book-Ratings.csv", 'r', 'utf8')
for line in f:
i += 1
#separate line into fields
fields = line.split(';')
user = fields[0].strip('"')
book = fields[1].strip('"')
rating = int(fields[2].strip().strip('"'))
if user in self.data:
currentRatings = self.data[user]
else:
currentRatings = {}
currentRatings[book] = rating
self.data[user] = currentRatings
f.close()
#
# 将书籍信息存入self.productid2name
# 包括isbn号、书名、作者等
#
f = codecs.open(path + "BX-Books.csv", 'r', 'utf8')
for line in f:
i += 1
#separate line into fields
fields = line.split(';')
isbn = fields[0].strip('"')
title = fields[1].strip('"')
author = fields[2].strip().strip('"')
title = title + ' by ' + author
self.productid2name[isbn] = title
f.close()
#
# 将用户信息存入self.userid2name和self.username2id
#
f = codecs.open(path + "BX-Users.csv", 'r', 'utf8')
for line in f:
i += 1
#print(line)
#separate line into fields
fields = line.split(';')
userid = fields[0].strip('"')
location = fields[1].strip('"')
if len(fields) > 3:
age = fields[2].strip().strip('"')
else:
age = 'NULL'
if age != 'NULL':
value = location + ' (age: ' + age + ')'
else:
value = location
self.userid2name[userid] = value
self.username2id[location] = userid
f.close()
print(i)
def pearson(self, rating1, rating2):
sum_xy = 0
sum_x = 0
sum_y = 0
sum_x2 = 0
sum_y2 = 0
n = 0
for key in rating1:
if key in rating2:
n += 1
x = rating1[key]
y = rating2[key]
sum_xy += x * y
sum_x += x
sum_y += y
sum_x2 += pow(x, 2)
sum_y2 += pow(y, 2)
if n == 0:
return 0
# 计算分母
denominator = (sqrt(sum_x2 - pow(sum_x, 2) / n)
* sqrt(sum_y2 - pow(sum_y, 2) / n))
if denominator == 0:
return 0
else:
return (sum_xy - (sum_x * sum_y) / n) / denominator
def computeNearestNeighbor(self, username):
"""获取邻近用户"""
distances = []
for instance in self.data:
if instance != username:
distance = self.fn(self.data[username],
self.data[instance])
distances.append((instance, distance))
# 按距离排序,距离近的排在前面
distances.sort(key=lambda artistTuple: artistTuple[1],
reverse=True)
return distances
def recommend(self, user):
"""返回推荐列表"""
recommendations = {}
# 首先,获取邻近用户
nearest = self.computeNearestNeighbor(user)
#
# 获取用户评价过的商品
#
userRatings = self.data[user]
#
# 计算总距离
totalDistance = 0.0
for i in range(self.k):
totalDistance += nearest[i][1]
# 汇总K邻近用户的评分
for i in range(self.k):
# 计算饼图的每个分片
weight = nearest[i][1] / totalDistance
# 获取用户名称
name = nearest[i][0]
# 获取用户评分
neighborRatings = self.data[name]
# 获得没有评价过的商品
for artist in neighborRatings:
if not artist in userRatings:
if artist not in recommendations:
recommendations[artist] = (neighborRatings[artist]
* weight)
else:
recommendations[artist] = (recommendations[artist]
+ neighborRatings[artist]
* weight)
# 开始推荐
recommendations = list(recommendations.items())
recommendations = [(self.convertProductID2name(k), v)
for (k, v) in recommendations]
# 排序并返回
recommendations.sort(key=lambda artistTuple: artistTuple[1],
reverse = True)
# 返回前n个结果
return recommendations[:self.n]
运行示例
首先构建一个推荐类,然后获取推荐结果:
>>> r = recommender(users)
>>> r.recommend('Jordyn')
[('Blues Traveler', 5.0)]
>>> r.recommend('Hailey')
[('Phoenix', 5.0), ('Slightly Stoopid', 4.5)]
新的数据集
现在让我们使用一个更为真实的数据集。Cai-Nicolas Zeigler从图书漂流站收集了超过100万条评价数据——278,858位用户为271,379本书打了分。这份数据(匿名)可以从这个地址获得,有SQL和CSV两种格式。由于特殊符号的关系,这些数据无法直接加载到Python里。我做了一些清洗,可以从这里下载。
CSV文件包含了三张表:
- 用户表,包括用户ID、位置、年龄等信息。其中用户的姓名已经隐去;
- 书籍表,包括ISBN号、标题、作者、出版日期、出版社等;
- 评分表,包括用户ID、书籍ISBN号、以及评分(0-10分)。
上文Python代码中的loadBookDB方法可以加载这些数据,用法如下:
>>> r.loadBookDB('/Users/raz/Downloads/BX-Dump/')
1700018
>>> r.recommend('171118')
注意 由于数据集比较大,大约需要几十秒的时间加载和查询。
项目实践
只有运行调试过书中的代码后才能真正掌握这些方法,以下是一些实践建议:
- 实现一个计算曼哈顿距离和欧几里得距离的方法;
- 本书的网站上有一个包含25部电影评价的数据集,实现一个推荐算法。