第二部分 分类
十三、KNN 分类入门
欢迎阅读第十三篇机器学习系列讲义。我们开始了一个全新的部分:分类。这面,我们会涉及两个主要的分类算法:K 最近邻和支持向量机(SVM)。这两个算法都是分类算法,它们的工作方式不同。
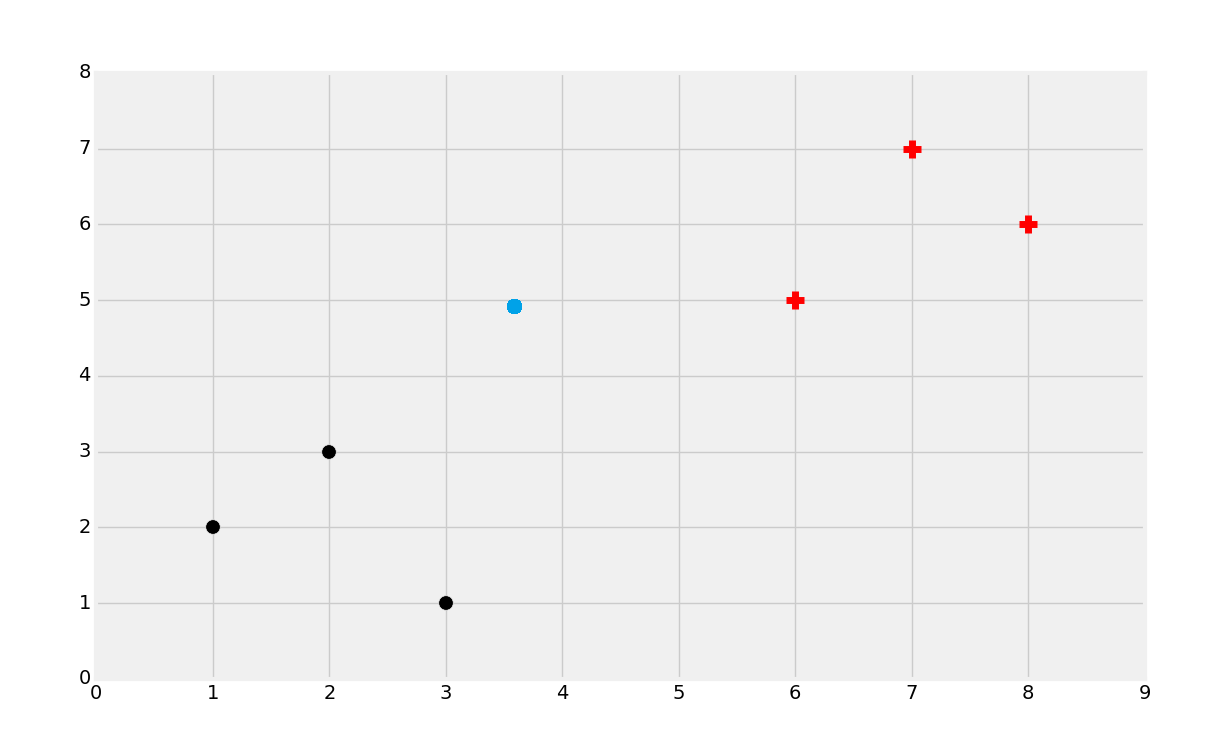
首先,让我们考虑一个数据集,创建下面的图像:
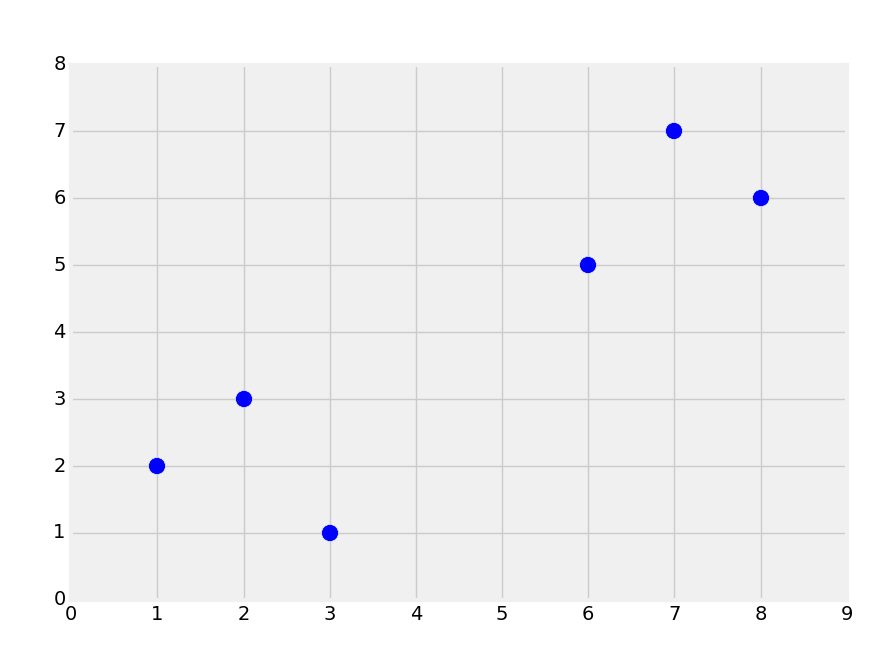
直观上,你应该能够看到两个组。但是,分类是监督式机器学习。当我们将数据提供给机器学习算法的时候,我们实际上已经告诉它组的存在,以及哪个数据属于哪个组。一个机器学习的相似形式是聚类,其中你让机器寻找组,但它是非监督机器学习算法,后面我们会降到。所以,使用监督式机器学习,我们需要拥有预置标签的数据用于训练,像这样:
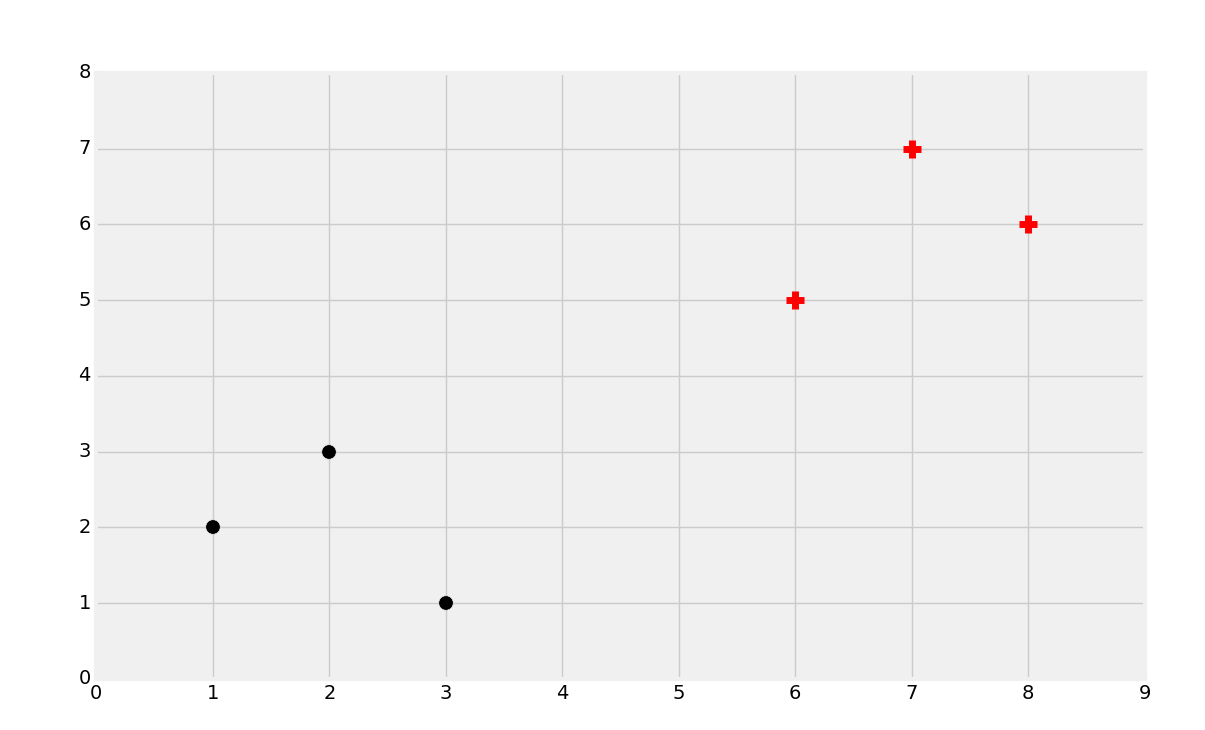
这里我们拥有黑的点和红的点。分类的目标就是拿已知的数据训练机器,就像这样,使机器能够识别新数据的分类(红的还是黑的)。例如,我们会处理乳腺肿瘤的数据,来基于一些属性尝试判断是良性的还是恶性的。我们实现它的方式,就是获取已知的样本属性,例如大小、形状作为特征,标签或者分类就是良性或者恶性。这里,我们可以根据纵六的相同属性来评估未来的肿瘤,并且预测是良性还是恶性。
所以,分类的目标就是识别下面的点属于哪个类:
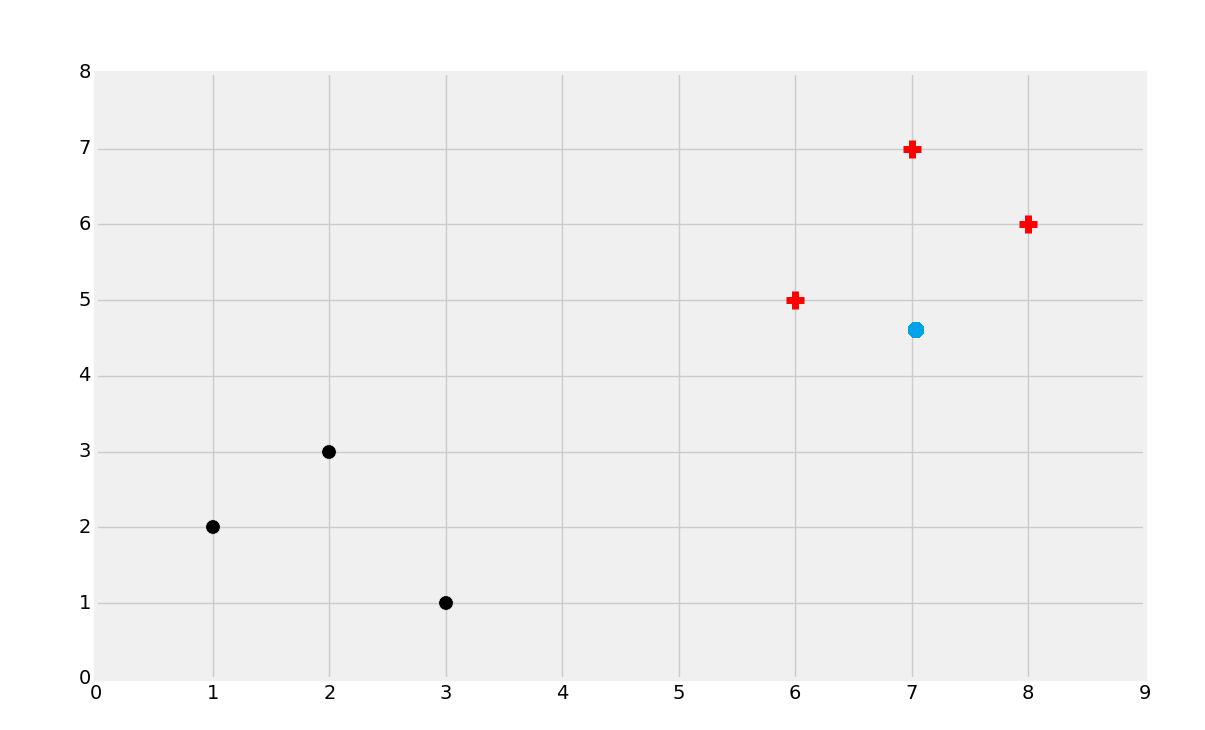
你可能能猜到它是红的类,但是为什么呢?尝试为自己定义这里有什么参数。下面这种情况呢?
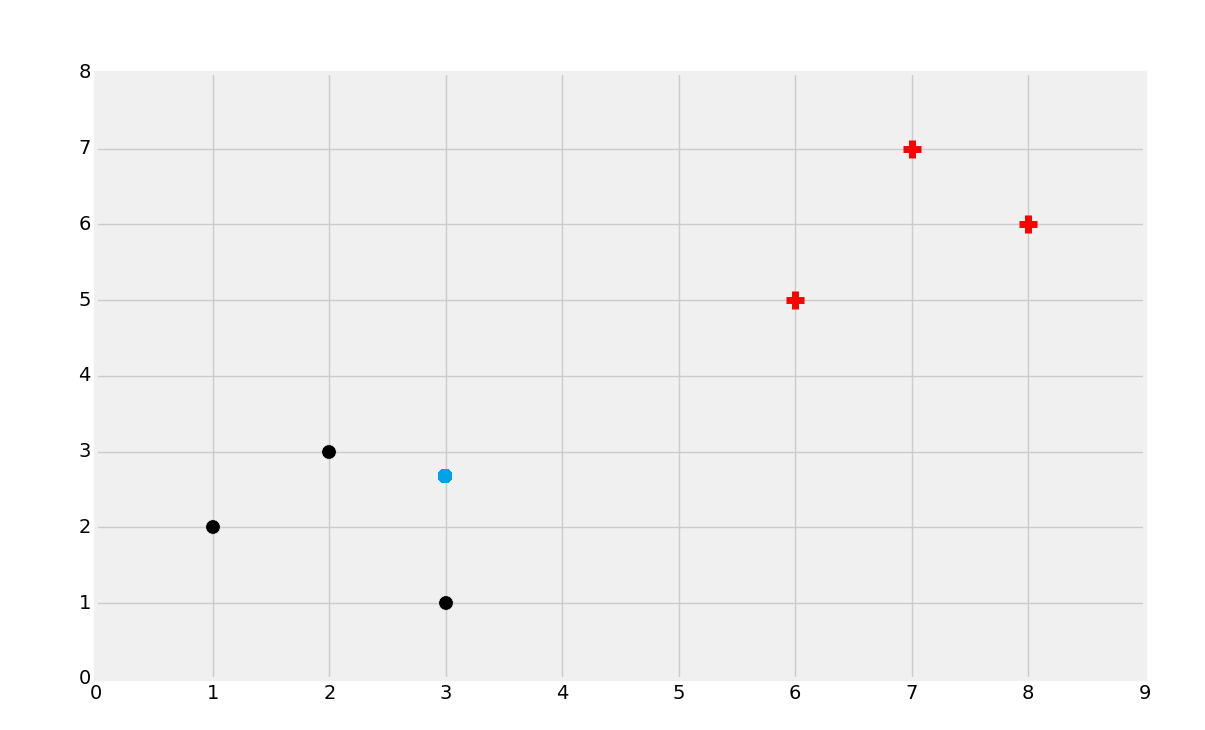
第二种情况中我们可能选取黑色。同样,尝试定义为啥这么选择。最后,如果是这样:
这种情况比较复杂,尝试选取一种分类。
大多数人都会选择黑色。无论哪种,考虑为什么你会做出这种选择。多数人会根据近似性对数据集分组。直觉上它是最有意义的。如果你拿尺子画出它到最近的黑色点的直线,之后画出它到最近的红色点的直线,你就会发现黑色点更近一些。与之相似,当数据点距离一个分组比另一个更近时,你就会基于近似性做出判断。因此 KNN 机器学习算法就诞生了。
KNN 是个简单高效的机器学习分类算法。如果这非常简单,就像我们看到的那样,我们为什么需要一个算法,而不是直接拿眼睛看呢?就像回归那样,机器可以计算得更快,处理更大的数据集,扩展,以及更重要的是,处理更多维度,例如 100 维。
它的工作方式就是它的名字。K 就是你选取的数量,近邻就是已知数据中的相邻数据点。我们寻找任意数量的“最近”的相邻点。假设K=3,所以我们就寻找三个最近的相邻点。例如:
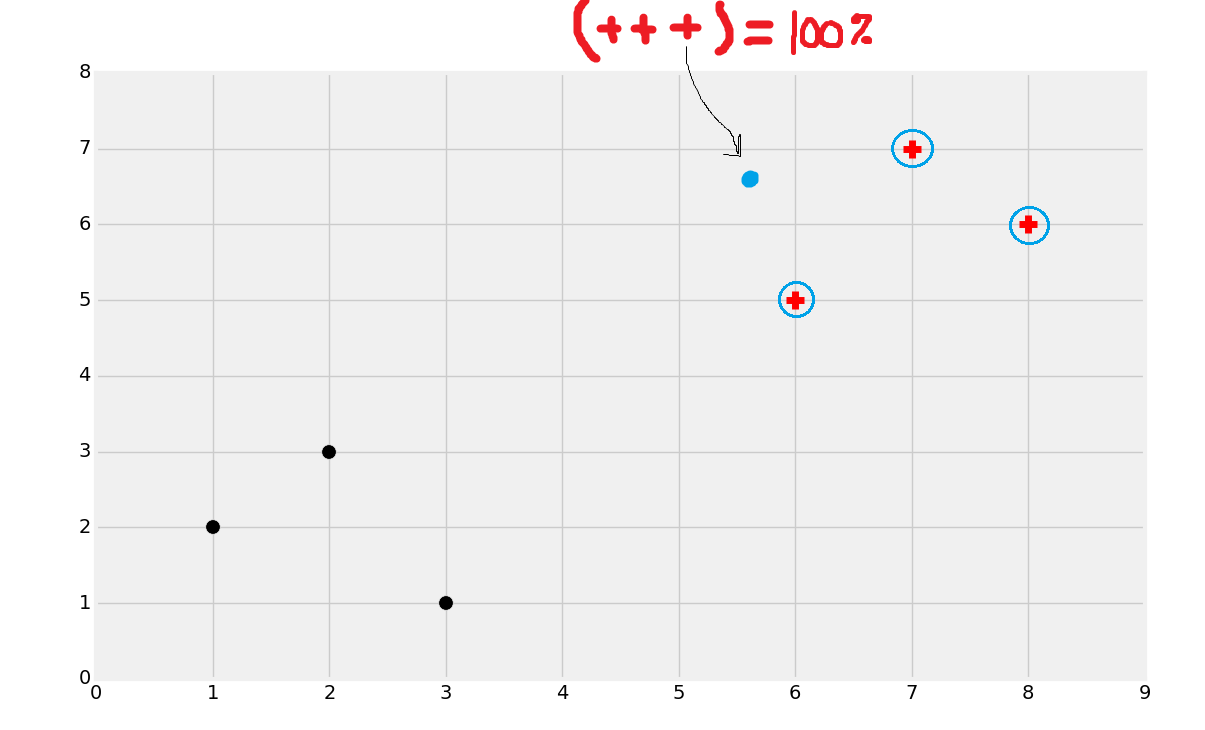
上面的图中,我圈出了三个最近的相邻点。这里,所有三个点都是红色分类。KNN 会基于相邻点进行计数。所有三个近邻都是红色,所以它 100% 是红色分类。如果两个近邻都是红色,一个是黑色,我们也将其分类为红色,只是置信度就少了。要注意,由于计数的本质,你会更希望使用奇数 K,否则会产生 50:50 的情况。有一种方式在距离上应用权重,来惩罚那些更远的点,所以你就可以使用偶数的 K 值了。
下一个教程中,我们会涉及到 Scikit 的 KNN 算法,来处理乳腺肿瘤数据,之后我们会尝试自己来编写这个算法。
十四、对数据使用 KNN
欢迎阅读第十四个部分。上一个部分我们介绍了分类,它是一种机器学习的监督算法,并且解释了 KNN 算法的直觉。这个教程中,我们打算使用 Sklearn,讲解一个简单的算法示例,之后在后面的教程中,我们会构建我们自己的算法来更多了解背后的工作原理。
为了使用例子说明分类,我们打算使用乳腺肿瘤数据集,它是 UCI 所贡献的数据集,从威斯康星大学收集。UCI 拥有庞大的机器学习仓库。这里的数据集组织为经常使用的机器学习算法类型、数据类型、属性类型、主题范围以及其它。它们对教学和机器学习算法开发都很实用。我自己经常浏览那里,非常值得收藏。在乳腺肿瘤数据集的页面,选择Data Folder链接。之后,下载breast-cancer-wisconsin.data和breast-cancer-wisconsin.names。这些可能不能下载,而是会在浏览器中展示。如果是这样右键点击“另存为”。
下载之后,打开breast-cancer-wisconsin.names文件。查看文件,向下滚动 100 行,我们就能获取属性(列)的名称、使用这些信息,我们打算手动将这些标签添加到breast-cancer-wisconsin.data文件中。打开它,并输入新的第一行:
id,clump_thickness,uniform_cell_size,
uniform_cell_shape,marginal_adhesion,
single_epi_cell_size,bare_nuclei,bland_chromation,
normal_nucleoli,mitoses,class
之后,你应该会思考,我们的特征和标签应该是什么。我们尝试对数据进行分类,所以很显然分类就是这些属性会导致良性还是恶性。同样,大多数这些属性看起来都是可用的,但是是否有任何属性与其它属性类似,或者是无用的?ID 属性并不是我们打算扔给分类器的东西。
缺失或者损坏的数据:这个数据集拥有一些缺失数据,我们需要清理。让我们以导入来开始,拉取数据,之后做一些清理:
import numpy as np
from sklearn import preprocessing, cross_validation, neighbors
import pandas as pd
df = pd.read_csv('breast-cancer-wisconsin.data.txt')
df.replace('?',-99999, inplace=True)
df.drop(['id'], 1, inplace=True)
在读取数据之后,我们注意到,有一些列存在缺失数据。这些缺失数据以?填充。.names文件告诉了我们,但是我们最终可以通过错误来发现,如果我们尝试将这些信息扔给分类为。这个时候,我们选择将缺失数据填充为 -99999 值。你可以选择你自己的方法来处理缺失数据,但是在真实世界中,你可能发现 50% 或者更多记录,一个或多个列都含有缺失数据。尤其是,如果你使用可扩展的属性来收集数据。-99999 并不完美,但是它足够有效了。下面,我们丢弃了 ID 列。完成之后,我们会注释掉 ID 列的丢弃,只是看看包含他可能有哪些影响。
下面,我们定义我们的特征和标签。
特征X是除了分类的任何东西。调用df.drop会返回一个新的 DataFrame,不带丢弃的列。标签y仅仅是分类列。
现在我们创建训练和测试样本,使用 Sklearn 的cross_validation.train_test_split。
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.2)
定义分类器:
clf = neighbors.KNeighborsClassifier()
这里,我们使用 KNN 分类器。
训练分类器:
clf.fit(X_train, y_train)
测试:
accuracy = clf.score(X_test, y_test)
print(accuracy)
结果应该是 95%,并且开箱即用,无需任何调整。非常棒。让我们展示一下,当我们注释掉 ID 列,包含一些无意义和误导性的数据之后,会发生什么。
import numpy as np
from sklearn import preprocessing, cross_validation, neighbors
import pandas as pd
df = pd.read_csv('breast-cancer-wisconsin.data.txt')
df.replace('?',-99999, inplace=True)
#df.drop(['id'], 1, inplace=True)
X = np.array(df.drop(['class'], 1))
y = np.array(df['class'])
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.2)
clf = neighbors.KNeighborsClassifier()
clf.fit(X_train, y_train)
accuracy = clf.score(X_test, y_test)
print(accuracy)
影响很令人吃惊,准确率从 95% 降到了 60%。在未来,如果 AI 通知了这个星球,要注意你只需要给它一些无意义的属性来智取它。非常有意思,添加噪声是一种损害你的算法的方式。当你和你的机器人霸主较量时,分辨有意义和恶意的噪声会节省你的时间。
下面你可以大致猜测,我们如何做预测,如果你遵循了 Sklearn 的教程。首先,我们需要一些沿革本数据。我们可以自己编。例如,我们会查看样本文件的某一行。你可以添加噪声来执行进一步的分析,假设标准差不是那么离谱。这么做也比较安全,由于你并不在篡改的数据上训练,你仅仅做了测试。我会通过编造一行来手动实现它。
example_measures = np.array([4,2,1,1,1,2,3,2,1])
你可以尽管在文档中搜索特征列表。它不存在。现在你可以:
prediction = clf.predict(example_measures)
print(prediction)
或者取决于你的阅读时间,你可能不能这么做。在这么做的时候,我得到了一个警告:
DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and will raise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample.
好的,没有问题。我们只拥有一个特征吗?不是。我们只拥有一个记录吗?是的。所以我们使用X.reshape(1, -1)。
example_measures = np.array([4,2,1,1,1,2,3,2,1])
example_measures = example_measures.reshape(1, -1)
prediction = clf.predict(example_measures)
print(prediction)
# 0.95
# [2]
这里的第一个输出是准确率(95%)和预测(2)。这就是我们的伪造数据的建模。
如果我们有两条呢?
example_measures = np.array([[4,2,1,1,1,2,3,2,1],[4,2,1,1,1,2,3,2,1]])
example_measures = example_measures.reshape(2, -1)
prediction = clf.predict(example_measures)
print(prediction)
忽略这个硬编码。如果我们不知道有几何样例会怎么样?
example_measures = np.array([[4,2,1,1,1,2,3,2,1],[4,2,1,1,1,2,3,2,1]])
example_measures = example_measures.reshape(len(example_measures), -1)
prediction = clf.predict(example_measures)
print(prediction)
你可以看到,KNN 算法的实现不仅仅很简单,而且这里也很准确。下一个教程中,我们打算从零构建我们自己的 KNN 算法,而不是使用 Sklearn,来尝试了解更多算法的东西,理解它的工作原理,最重要的是,了解它的陷阱。
十五、对数据使用 KNN
欢迎阅读第十五篇教程,其中我们当前涉及到使用 KNN 算法来分类。上一篇教程中,我们涉及到如何使用 Sklearn 的 KNN 算法来预测良性或者恶性肿瘤,基于肿瘤的属性,准确率有 95%。现在,我们打算深入 KNN 的工作原理,以便完全理解算法本身,来使其更好为我们工作。
我们会回到我们的乳腺肿瘤数据集,对其使用我们自定义 KNN 算法,并将其与 Sklearn 的比较,但是我们打算首先以一个非常简单的理论开始。KNN 基于近似性,不是分组,而是单独的点。所以,所有这种算法所做的,实际上是计算点之间的距离,并且之后选取距离最近的前 K 个点的最常出现的分类。有几种方式来计算平面上的距离,他们中许多都可以在这里使用,但是最常使用的版本是欧氏距离,以欧几里得命名。他是一个著名的数学家,被称为几何之父,他编写了《几何原本》,被称为数学家的圣经。欧氏距离为:
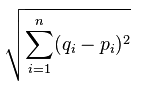
所以这是什么意思?基本上,它是每个点之间距离的平方和的平方根。在 Python 的术语中,是这样:
plot1 = [1,3]
plot2 = [2,5]
euclidean_distance = sqrt( (plot1[0]-plot2[0])**2 + (plot1[1]-plot2[1])**2 )
这里距离是 2.236。
这就是 KNN 背后的基本数学原理了,现在我们仅仅需要构建一个系统来处理算法的剩余部分,例如寻找最近距离,它们的分组,然后是计数。
十六、从零创建 KNN 分类器:第一部分
欢迎阅读第十六个部分,我们现在涉及到 KNN 算法的分类。在上一个教程中,我们涉及到了欧氏距离,现在我们开始使用纯粹的 Python 代码来建立我们自己的简单样例。
最开始,让我们导入下列东西并为 Matplotlib 设置一个样式。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
import warnings
from math import sqrt
from collections import Counter
style.use('fivethirtyeight')
我们打算使用警告来避免使用比分组数量更低的 K 值,至少是最开始(因为我会展示一个更加高效的方法),之后对集合计数来获取出现次数最多的分类。
下面,我们创建一些数据:
dataset = {'k':[[1,2],[2,3],[3,1]], 'r':[[6,5],[7,7],[8,6]]}
new_features = [5,7]
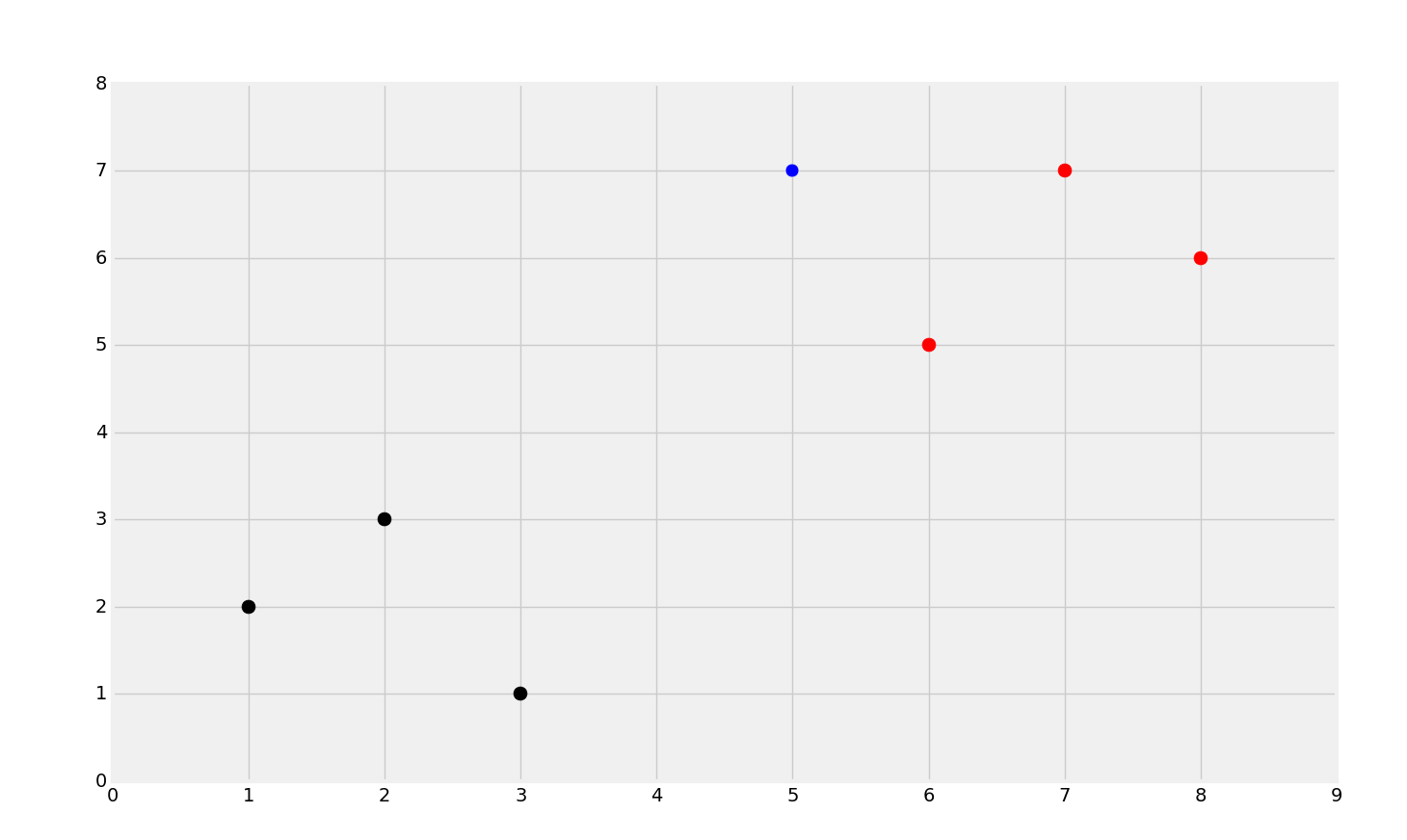
这个数据集只是个 Python 字典,键是点的颜色(将这些看做分类),值是属于这个分类的数据点。如果你回忆我们的乳腺肿瘤数据集,分类都是数字,通常 Sklearn 只能处理数字。例如,向量翻译为任意数字2,而恶性翻译为任意数字4,而不是一个字符串。这是因为,Sklearn 只能使用数字,但是你并不一定要使用数字来代表分类。下面,我们创建简单的数据集5, 7,用于测试。我们可以这样来快速绘图:
[[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in dataset[i]] for i in dataset]
plt.scatter(new_features[0], new_features[1], s=100)
plt.show()
[[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in dataset[i]] for i in dataset]这一行和下面这个相同:
for i in dataset:
for ii in dataset[i]:
plt.scatter(ii[0],ii[1],s=100,color=i)
你可以看到红色和黑色的明显分组,并且我们还有蓝色的点,它是new_features,我们打算对其分类。
我们拥有了数据,现在我们打算创建一些函数,来分类数据。
def k_nearest_neighbors(data, predict, k=3):
return vote_result
这就是我们的框架,从这里开始。我们想要一个函数,它接受要训练的数据,预测的数据,和 K 值,它的默认值为 3。
下面,我们会开始填充函数,首先是一个简单的警告:
def k_nearest_neighbors(data, predict, k=3):
if len(data) >= k:
warnings.warn('K is set to a value less than total voting groups!')
return vote_result
如果选取的最近邻的数量小于或等于分类数量,那么就给出警告(因为这样会产生偏差)。
现在,如何寻找最近的三个点呢?是否有一些用于搜索的魔法呢?没有,如果有的话,也是很复杂而。为什么呢?KNN 的工作原理是,我们需要将问题中的数据与之前的数据比较,之后才能知道最近的点是什么。因此,如果你的数据越多,KNN 就越慢。我们这里告一段落,但是要考虑是否有方法来加速这个过程。
十七、从零创建 KNN 分类器:第二部分
欢迎阅读第十七个部分,我们正在讲解 KNN 算法的分类。上一个教程中,我们开始构建我们的 KNN 示例,这里我们将其完成。
我处理它的方式,就是首先创建一个 Python 列表,它包含另一个列表,里面包含数据集中每个点的距离和分类。一旦填充完毕,我们就可以根据距离来排序列表,截取列表的前 K 个值,找到出现次数最多的,就找到了答案。
def k_nearest_neighbors(data, predict, k=3):
if len(data) >= k:
warnings.warn('K is set to a value less than total voting groups!')
distances = []
for group in data:
for features in data[group]:
euclidean_distance = sqrt( (features[0]-predict[0])**2 + (features[1]-predict[1])**2 )
distances.append([euclidean_distance,group])
有一种方式来计算欧氏距离,最简洁的方式就是遵循定义。也就是说,使用 NumPy 会更快一点。由于 KNN 是一种机器学习的爆破方法,我们需要我们能得到的所有帮助。因此,我们可以将函数修改一点。一个选项是:
euclidean_distance = np.sqrt(np.sum((np.array(features)-np.array(predict))**2))
print(euclidean_distance)
这还是很清楚,我们刚刚使用了 NumPy 版本。NumPy 使用 C 优化,是个非常高效的库,很多时候允许我们计算更快的算术。也就是说,NumPy 实际上拥有大量的线性代数函数。例如,这是范数:
euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict))
print(euclidean_distance)
欧式距离度量两个端点之间的线段长度。欧几里得范数度量向量的模。向量的模就是它的长度,这个是等价的。名称仅仅告诉你你所在的控件。
我打算使用后面那一个,但是我会遵循我的约定,使其易于拆解成代码。如果你不了解 NumPy 的内建功能,你需要去了解如何使用。
现在,for循环之外,我们得到了距离列表,它包含距离和分类的列表。我们打算对列表排序,之后截取前 K 个元素,选取下标 1,它就是分类。
votes = [i[1] for i in sorted(distances)[:k]]
上面,我们遍历了排序后的距离列表的每个列表。排序方法会(首先)基于列表中每个列表的第一个元素。第一个元素是距离,所以执行orted(distances)之后我们就按照从小到大的距离排序了列表。之后我们截取了列表的[:k],因为我们仅仅对前 K 个感兴趣。最后,在for循环的外层,我们选取了i[1],其中i就是列表中的列表,它包含[diatance, class](距离和分类的列表)。按照距离排序之后,我们无需再关心距离,只需要关心分类。
所以现在有三个候选分类了。我们需要寻找出现次数最多的分类。我们会使用 Python 标准库模块collections.Counter。
vote_result = Counter(votes).most_common(1)[0][0]
Collections会寻找最常出现的元素。这里,我们想要一个最常出现的元素,但是你可以寻找前 3 个或者前x个。如果没有[0][0]这部分,你会得到[('r', 3)](元素和计数的元组的列表)。所以[0][0]会给我们元组的第一个元素。你看到的 3 是'r'的计数。
最后,返回预测结果,就完成了。完整的代码是:
def k_nearest_neighbors(data, predict, k=3):
if len(data) >= k:
warnings.warn('K is set to a value less than total voting groups!')
distances = []
for group in data:
for features in data[group]:
euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict))
distances.append([euclidean_distance,group])
votes = [i[1] for i in sorted(distances)[:k]]
vote_result = Counter(votes).most_common(1)[0][0]
return vote_result
现在,如果我们打算基于我们之前所选的点,来做预测:
result = k_nearest_neighbors(dataset, new_features)
print(result)
非常肯定,我得到了r,这就是预期的值。让我们绘制它吧。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
import warnings
from math import sqrt
from collections import Counter
style.use('fivethirtyeight')
def k_nearest_neighbors(data, predict, k=3):
if len(data) >= k:
warnings.warn('K is set to a value less than total voting groups!')
distances = []
for group in data:
for features in data[group]:
euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict))
distances.append([euclidean_distance,group])
votes = [i[1] for i in sorted(distances)[:k]]
vote_result = Counter(votes).most_common(1)[0][0]
return vote_result
dataset = {'k':[[1,2],[2,3],[3,1]], 'r':[[6,5],[7,7],[8,6]]}
new_features = [5,7]
[[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in dataset[i]] for i in dataset]
# same as:
##for i in dataset:
## for ii in dataset[i]:
## plt.scatter(ii[0],ii[1],s=100,color=i)
plt.scatter(new_features[0], new_features[1], s=100)
result = k_nearest_neighbors(dataset, new_features)
plt.scatter(new_features[0], new_features[1], s=100, color = result)
plt.show()
你可以看到,我们添加了新的点5, 7,它分类为红色的点,符合预期。
这只是小规模的处理,但是如果我们处理乳腺肿瘤数据集呢?我们如何和 Sklearn 的 KNN 算法比较?下一个教程中,我们会将算法用于这个数据集。
十八、测试 KNN 分类器
欢迎阅读第十八篇教程,我们刚刚编写了我们自己的 KNN 分类器算法,现在我们准备好了使用一些真实数据来测试它。开始,我们打算使用之前的乳腺肿瘤数据集。如果你没有它,返回教程 13 并抓取数据。
目前为止,我们的算法像这样处理数据:

其中蓝色的点是位置数据,运行算法,并正确分类数据:

现在,我们打算回顾乳腺肿瘤数据集,它记录肿瘤的属性变将它们按照良性还是恶性分类。Sklearn 的 KNN 分类器有 95% 的准确率,并且我们打算测试我们自己的算法。
我们会以下列代码开始:
import numpy as np
import warnings
from collections import Counter
import pandas as pd
import random
def k_nearest_neighbors(data, predict, k=3):
if len(data) >= k:
warnings.warn('K is set to a value less than total voting groups!')
distances = []
for group in data:
for features in data[group]:
euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict))
distances.append([euclidean_distance,group])
votes = [i[1] for i in sorted(distances)[:k]]
vote_result = Counter(votes).most_common(1)[0][0]
return vote_result
这应该看起来很熟悉。要注意我导入了 Pandas 和 random。我已经移除了 Matplotlib 的导入,因为我们不打算绘制任何东西。下面,我们打算加载数据:
df = pd.read_csv('breast-cancer-wisconsin.data.txt')
df.replace('?',-99999, inplace=True)
df.drop(['id'], 1, inplace=True)
full_data = df.astype(float).values.tolist()
这里,我们加载了数据,替换掉了问号,丢弃了 ID 列,并且将数据转危为列表的列表。要注意我们显式将 DataFrame 转换为浮点类型。出于一些原因,至少对于我来说,一些数据点仍然是数字,但是字符串数据类型并不是很好。
下面,我们打算把数据打乱,之后将其分割:
Next, we're going to shuffle the data, and then split it up:
random.shuffle(full_data)
test_size = 0.2
train_set = {2:[], 4:[]}
test_set = {2:[], 4:[]}
train_data = full_data[:-int(test_size*len(full_data))]
test_data = full_data[-int(test_size*len(full_data)):]
首先我们打乱了数据(它包含特征和标签)。之后我们为训练和测试集准备了一个字典用于填充。下面,我们指定了哪个是train_data,哪个是test_data。我们选取前 80% 作为train_data(逻辑是在后 20% 的地方分割),之后我们通过在后 20% 的地方分割,来创建test_data。
现在我们开始填充字典。如果不清楚的话,字典有两个键:2 和 4。2 是良性肿瘤(和实际数据集相同),4 是恶性肿瘤,也和数据集相同。我们将其硬编码,但是其他人可以选取分类,并像这样创建字典,它的键是分类中的唯一值。我们仅仅是使其简单。
for i in train_data:
train_set[i[-1]].append(i[:-1])
for i in test_data:
test_set[i[-1]].append(i[:-1])
现在我们填充了字典,我们拥有了测试集,其中键是分类,值是属性。
最后就是训练和测试的时候了。使用 KNN,这些步骤基本就完成了,因为训练步骤就是把点村进内存,测试步骤就是比较距离:
correct = 0
total = 0
for group in test_set:
for data in test_set[group]:
vote = k_nearest_neighbors(train_set, data, k=5)
if group == vote:
correct += 1
total += 1
print('Accuracy:', correct/total)
现在我们首先迭代测试集的分组(分类,2 或者 4,也是字典的键),之后我们遍历每个数据点,将数据点扔给k_nearest_neighbors,以及我们的训练集train_set,之后是我们的 K,它是 5。我选择了 5,纯粹是因为它是 SKlearn 的KNeighborsClassifier的默认值。所以我们的完整代码是:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
import warnings
from collections import Counter
#dont forget this
import pandas as pd
import random
style.use('fivethirtyeight')
def k_nearest_neighbors(data, predict, k=3):
if len(data) >= k:
warnings.warn('K is set to a value less than total voting groups!')
distances = []
for group in data:
for features in data[group]:
euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict))
distances.append([euclidean_distance,group])
votes = [i[1] for i in sorted(distances)[:k]]
vote_result = Counter(votes).most_common(1)[0][0]
return vote_result
df = pd.read_csv('breast-cancer-wisconsin.data.txt')
df.replace('?',-99999, inplace=True)
df.drop(['id'], 1, inplace=True)
full_data = df.astype(float).values.tolist()
random.shuffle(full_data)
test_size = 0.2
train_set = {2:[], 4:[]}
test_set = {2:[], 4:[]}
train_data = full_data[:-int(test_size*len(full_data))]
test_data = full_data[-int(test_size*len(full_data)):]
for i in train_data:
train_set[i[-1]].append(i[:-1])
for i in test_data:
test_set[i[-1]].append(i[:-1])
correct = 0
total = 0
for group in test_set:
for data in test_set[group]:
vote = k_nearest_neighbors(train_set, data, k=5)
if group == vote:
correct += 1
total += 1
print('Accuracy:', correct/total)
十九、KNN 的最终见解
既然我们了解了它的工作原理,这里我们打算涉及一些 KNN 算法的最终见解,包含 K 值,置信度,速度,以及算法的优点和缺点。
在执行 100 个样例的测试之后,Sklearn 的neighbors.KNeighborsClassifier分类器的准确率是 0.97,我们自己编写的分类器也一样。不要故步自封,因为这个算法非常简单和基础。KNN 分类器的真正价值并不在准确率上,而是它的速度。KNN 分类器的主要缺陷就是就是速度,你可以用它来执行操作。
对于速度,Sklearn 的 KNN 版本的每个周期是 0.044 秒,我们的是 0.55 秒。因此,虽然我们实现了相同的结果,我们比 Sklearn 慢很多。好的消息是,如果你对它们如何实现的感兴趣,你可以查看源代码、我们也提到了,我们也可以使用一个主流方式来提升速度。KNN 并不需要过多的训练。训练仅仅是将数据集加载到内存。你可以将数据集保留在内存中,但是 KNN 分类器的真正痛点就是对比每个数据集来寻找最近的那个。之后,如果你打算对 1000 个数据集分类,会发生什么呢?是的,一个选项是可以并发。串行执行它们没有任何好处。我们的方式是这样,仅仅使用一点点的处理器的能力。但是,我们可以一次性至少计算 100~200 个数据,即使是在便宜的处理器上。如果你打算了解如何并发,看一看这个并发教程。使用 Sklearn,KNN 分类器自带一个并行处理参数n_jobs。你可以将其设置为任何数值,你可以以这个线程数来并发。如果你打算一次运行 100 个操作,n_jobs=100。如果你仅仅打算运行尽可能做的操作,设置n_jobs=-1。阅读最近邻文档,你可以了解更多选项。有几种方式将你的数据与指定半径之内的数据对比,如果你对加速 KNN,以及 Sklearn 的 KNN 版本感兴趣,你可能想要看一看。
最后,我要讲的最后一点就是预测的置信度。有两种方式来度量置信度。一种是比较你预测对了多少个点,另一个是,检查计数的百分比。例如,你的算法准确率可能是 97%,但是对于一些分类,计数可能是 3 比 2。其中 3 是主流,它的占有率是 60%,而不是理想情况下的 100%。但是告诉别人它是否有癌症的话,就像自动驾驶汽车分辨一团土和毛毯上的孩子,你可能更希望是 100%。可能 60% 的计数就是 3% 的不准确度量的一部分。
好的,所以我们刚刚编写了准确率为 97% 的分类器,但是没有把所有事情都做好。KNN 非常拥有,因为它对线性和非线性数据都表现出色。主要的缺陷是规模、离群点和不良数据(要记得 ID 列的无效引入)。
我们仍然专注于监督式机器学习,特别是分类,我们下面打算设计支持向量机。
最后的代码:
import numpy as np
from math import sqrt
import warnings
from collections import Counter
import pandas as pd
import random
def k_nearest_neighbors(data, predict, k=3):
if len(data) >= k:
warnings.warn('K is set to a value less than total voting groups!')
distances = []
for group in data:
for features in data[group]:
euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict))
distances.append([euclidean_distance, group])
votes = [i[1] for i in sorted(distances)[:k]]
vote_result = Counter(votes).most_common(1)[0][0]
confidence = Counter(votes).most_common(1)[0][1] / k
return vote_result, confidence
df = pd.read_csv("breast-cancer-wisconsin.data.txt")
df.replace('?',-99999, inplace=True)
df.drop(['id'], 1, inplace=True)
full_data = df.astype(float).values.tolist()
random.shuffle(full_data)
test_size = 0.4
train_set = {2:[], 4:[]}
test_set = {2:[], 4:[]}
train_data = full_data[:-int(test_size*len(full_data))]
test_data = full_data[-int(test_size*len(full_data)):]
for i in train_data:
train_set[i[-1]].append(i[:-1])
for i in test_data:
test_set[i[-1]].append(i[:-1])
correct = 0
total = 0
for group in test_set:
for data in test_set[group]:
vote,confidence = k_nearest_neighbors(train_set, data, k=5)
if group == vote:
correct += 1
total += 1
print('Accuracy:', correct/total)
二十、支持向量机简介
欢迎阅读第二十篇。我们现在打算深入另一个监督式机器学习和分类的形式:支持向量机。
支持向量机,由 Vladimir Vapnik 在上个世纪 60 年代发明,但是 90 年代之前都被忽视,并且是最热门的机器学习分类器之一。
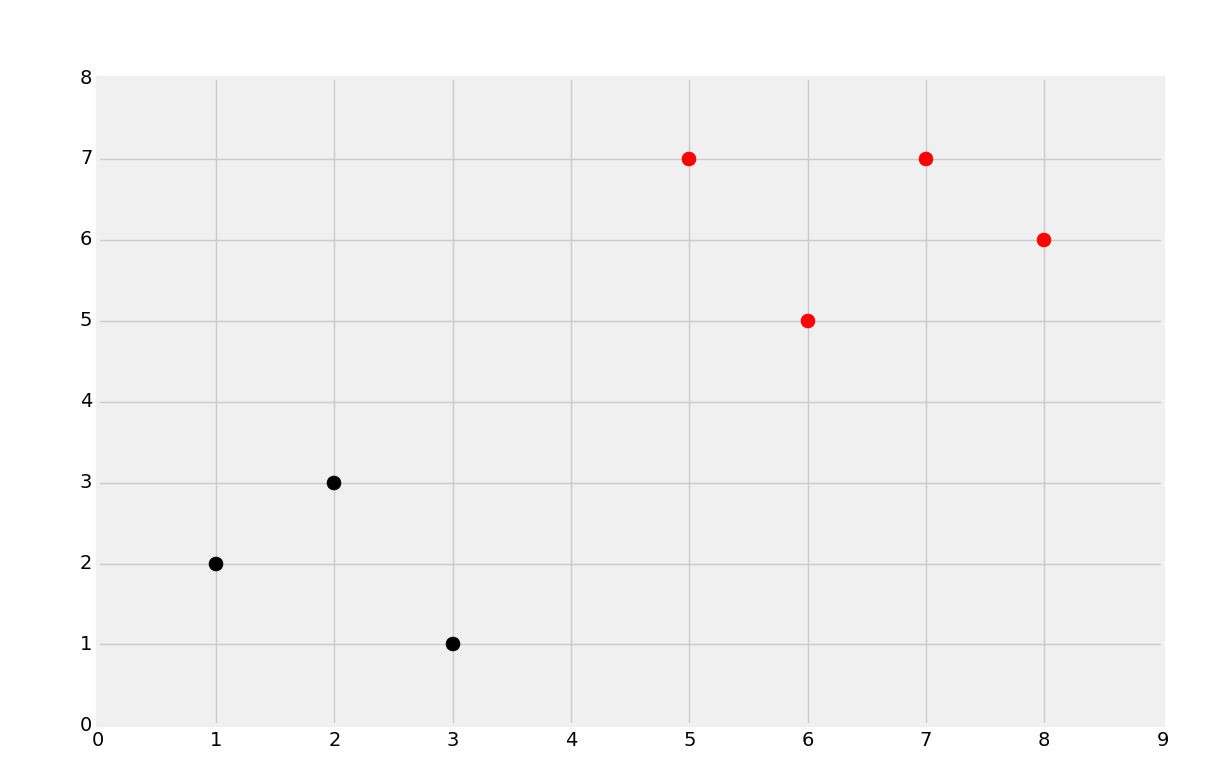
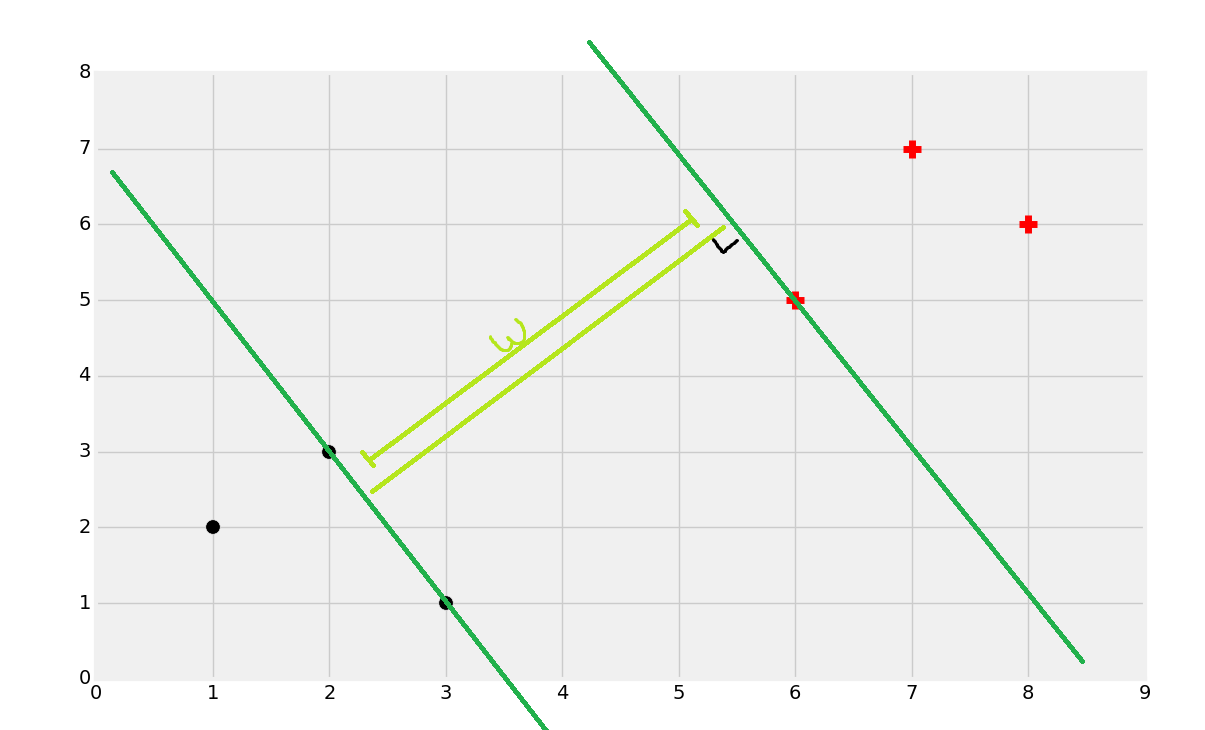
支持向量的目标就是寻找数据之间的最佳分割边界。在二维空间中,你可以将其看做分隔你的数据集的最佳拟合直线。使用支持向量机,我们在向量空间中处理问题,因此分隔直线实际上是个单独的超平面。最佳的分隔超平面定义为,支持向量之间间距“最宽”的超平面。超平面也可以叫做决策边界。最简单的讲解方式就是图片:
我们会使用上面的数据开始。我们注意到,之前最普遍的直觉就是,你会将一个新的点基于它的近邻来分类,这就是 KNN 的工作原理。这个方式的主要问题是,对于每个数据点,你将其与每个其它数据点比较,来获取距离,因为算法不能很好扩展,尽管准确率上很可靠。支持向量机的目标就是,一次性生成“最佳拟合”直线(实际上是个平面,甚至是个超平面),他可以最优划分数据。一旦计算出了超平面,我们就将其作为决策边界。我们这样做,因为决策边界划分两个分类的数据。一旦我们计算了决策边界,我们就再也不需要计算了,除非我们重新训练数据集。因此,算法易于扩展,不像 KNN 分类器。
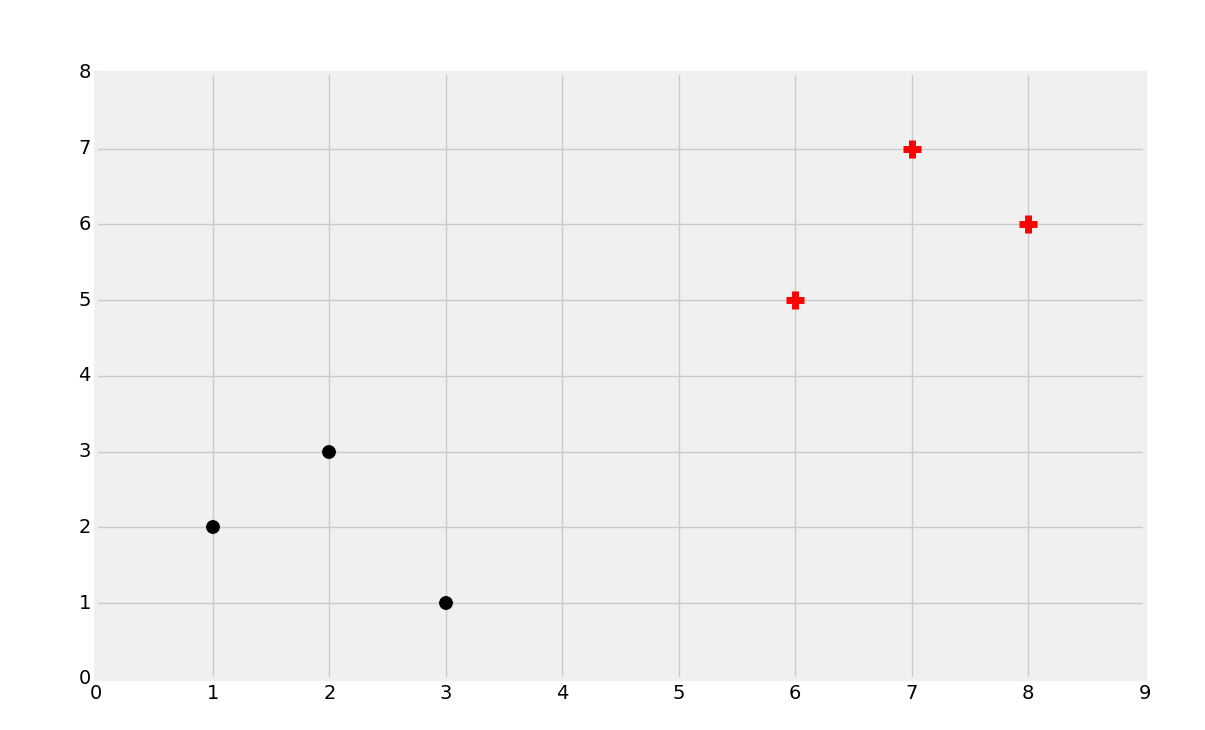
好奇之处在于,我们如何找出最佳分隔超平面?我们可以先使用眼睛来找。
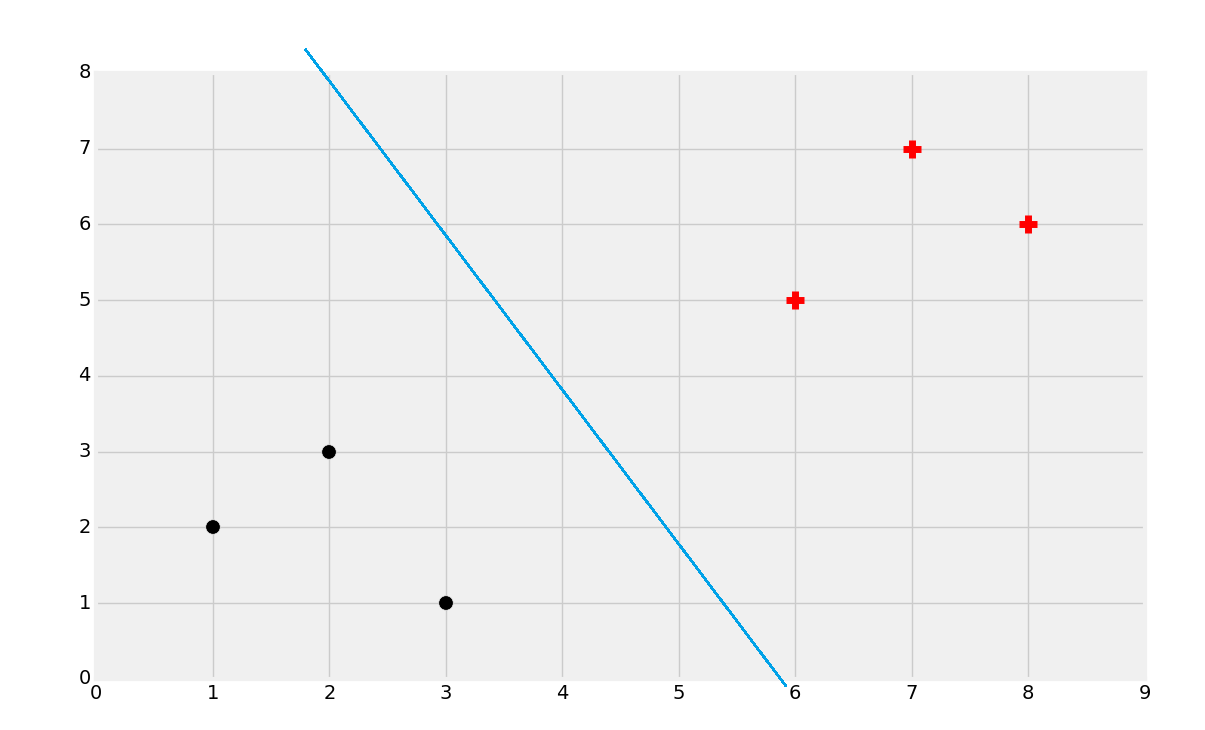
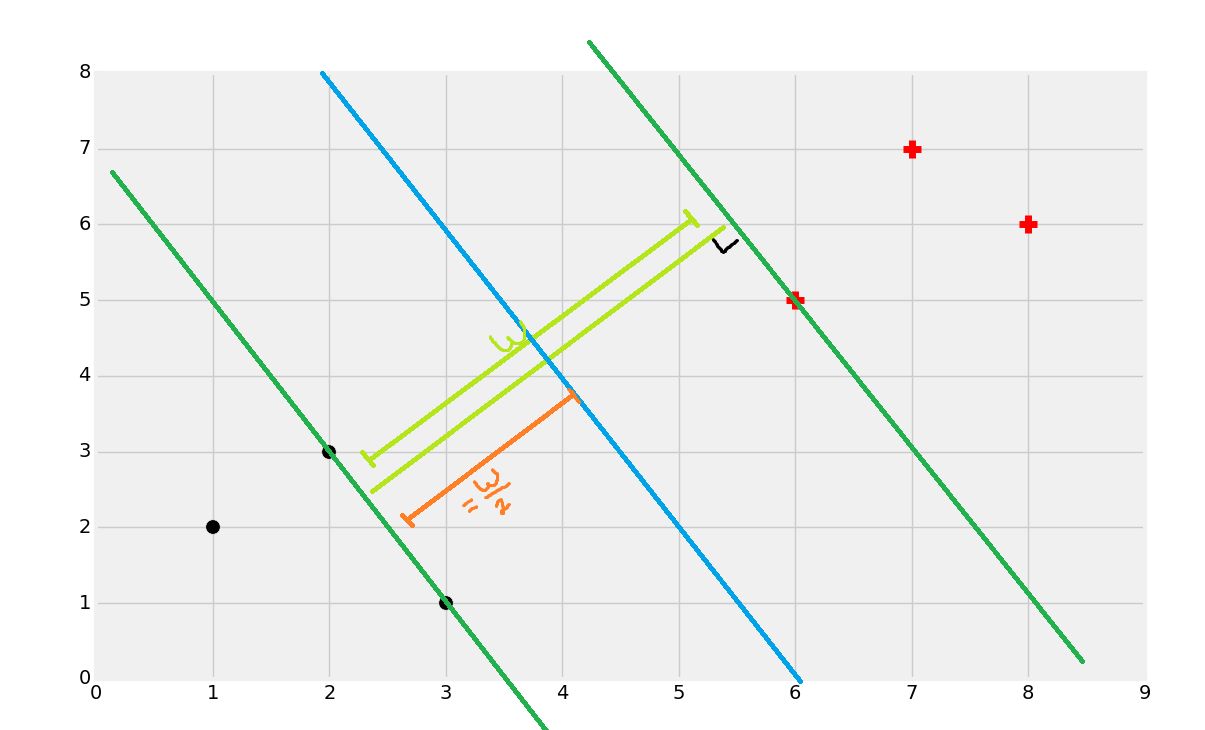
这几乎是争取的,但是如何寻找呢?首先寻找支持向量。
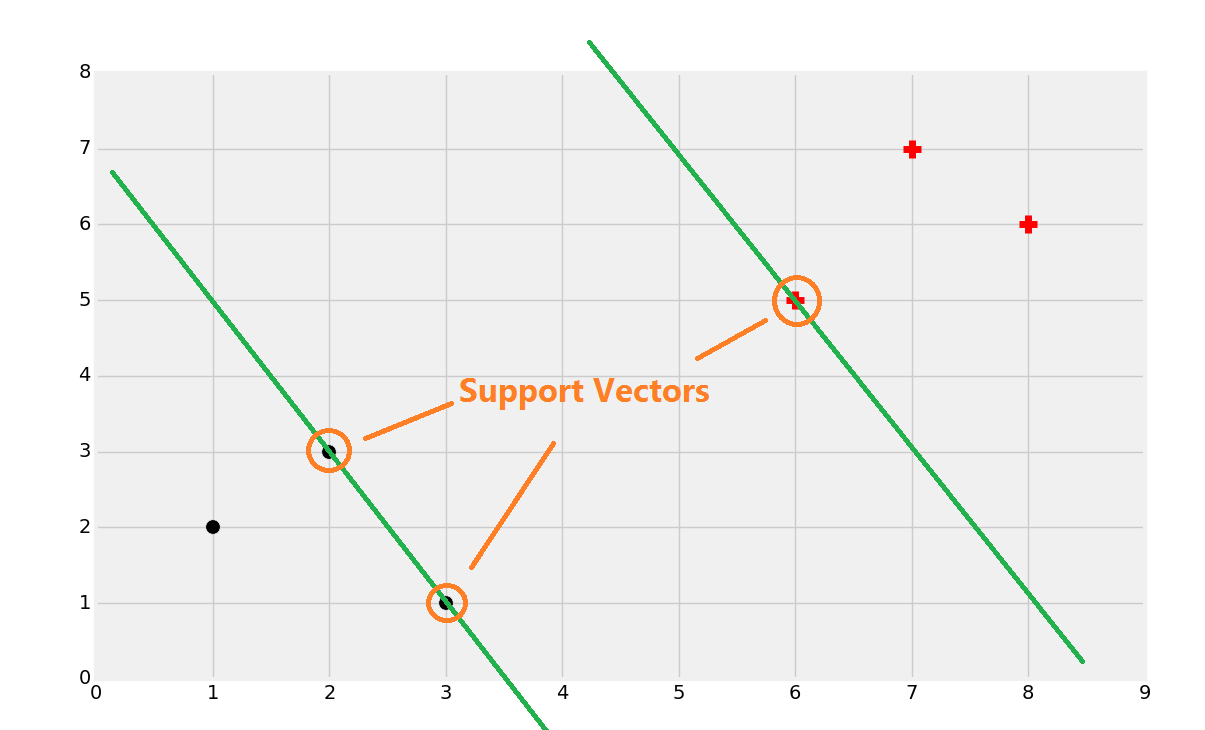
一旦你找到了支持向量,你就可以创建直线,最大分隔彼此。这里,我们可以通过计算总宽度来轻易找到决策边界。
一分为二。
你就会得到边界。
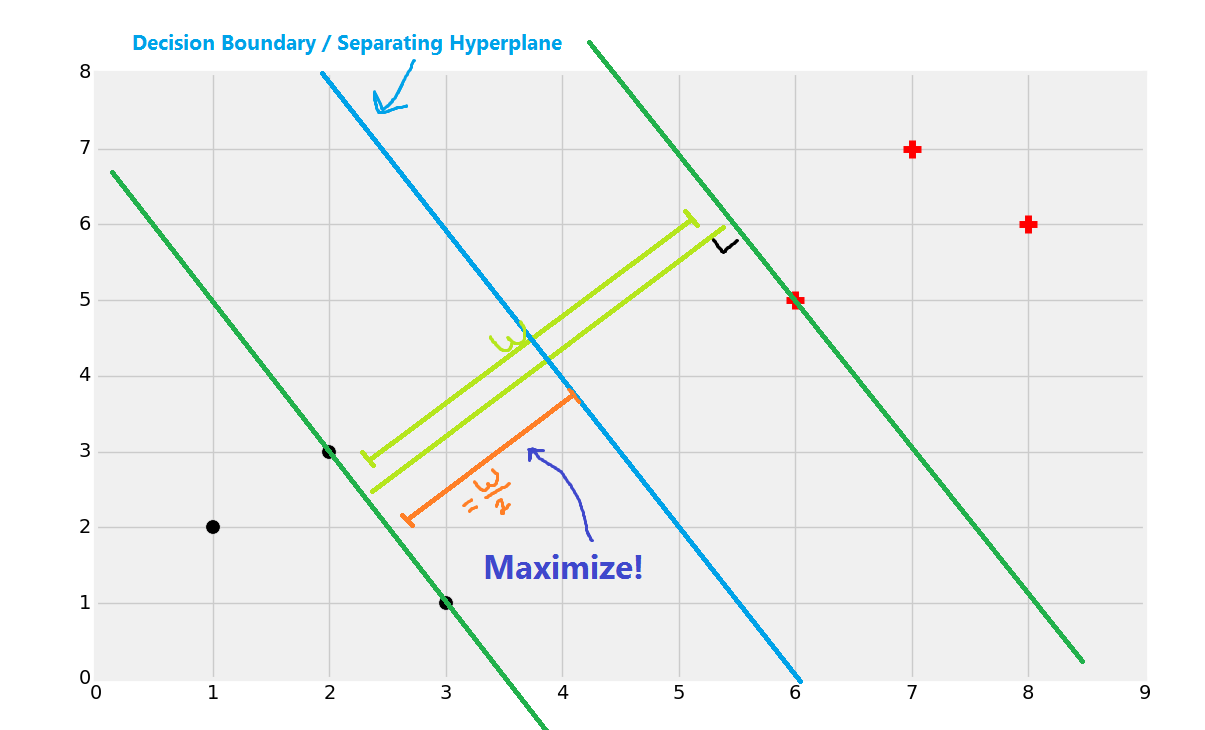
现在如果一个点位于决策边界或者分割超平面的左侧,我们就认为它是黑色分类,否则就是红色分类。
值得注意的是,这个方式本质上只能处理线性分隔的数据,如果你的数据是:
这里你能够创建分隔超平面嘛?不能。还有没有办法了?当我们深入支持向量机的时候,我会让你考虑这个问题。这里是使用 Sklearn 非常方便的原因。记得我们之前使用 Sklearn KNN 分类器的代码嘛?这里就是了。
import numpy as np
from sklearn import preprocessing, cross_validation, neighbors
import pandas as pd
df = pd.read_csv('breast-cancer-wisconsin.data.txt')
df.replace('?',-99999, inplace=True)
df.drop(['id'], 1, inplace=True)
X = np.array(df.drop(['class'], 1))
y = np.array(df['class'])
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.2)
clf = neighbors.KNeighborsClassifier()
clf.fit(X_train, y_train)
confidence = clf.score(X_test, y_test)
print(confidence)
example_measures = np.array([[4,2,1,1,1,2,3,2,1]])
example_measures = example_measures.reshape(len(example_measures), -1)
prediction = clf.predict(example_measures)
print(prediction)
我们只需要改动两个地方,第一个就是从sklearn导入svm。第二个就是使用支持向量分类为,它是svm.SVC。改动之后是:
import numpy as np
from sklearn import preprocessing, cross_validation, neighbors, svm
import pandas as pd
df = pd.read_csv('breast-cancer-wisconsin.data.txt')
df.replace('?',-99999, inplace=True)
df.drop(['id'], 1, inplace=True)
X = np.array(df.drop(['class'], 1))
y = np.array(df['class'])
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.2)
clf = svm.SVC()
clf.fit(X_train, y_train)
confidence = clf.score(X_test, y_test)
print(confidence)
example_measures = np.array([[4,2,1,1,1,2,3,2,1]])
example_measures = example_measures.reshape(len(example_measures), -1)
prediction = clf.predict(example_measures)
print(prediction)
# 0.978571428571
# [2]
取决于你爹随机样例,你应该得到 94% 到 99% ,平均值为 97%。同样,对操作计时,要记得我通过 Sklearn 执行 KNN 代码花费了 0.044 秒。使用svm.SVC,执行时间仅仅是 0.00951,在这个非常小的数据集上也有 4.6 倍。
所以我们可以认为,支持向量机似乎有同样的准确度,但是速度更快。要注意如果我们注释掉丢弃 ID 列的代码,准确率会降到 60%。支持向量机通常比 KNN 算法处理大量数据要好,并且处理离群点要好。但是,这个例子中,无意义数据仍然会误导它。我们之前使用默认参数,查看支持向量机的文档,确实有一些参数,我们不知道它们干什么用。在后面的教程中,我们打算深入支持向量机算法,以便我们能够实际理解所有这些参数的含义,以及它们有什么影响。虽然我们在这里告一段落,思考一下:如何处理非线性分隔,多个分类的数据和数据集(由于 SVM 是个二元分类器,也就是它生成直线来划分两个分组)。
二十一、向量基础
欢迎阅读第二十一篇教程,下面就是支持向量机的部分了。这个教程中,我们打算设计一些向量的基础,它们是支持向量机概念的组成部分。
首先,向量拥有模(大小)和方向:
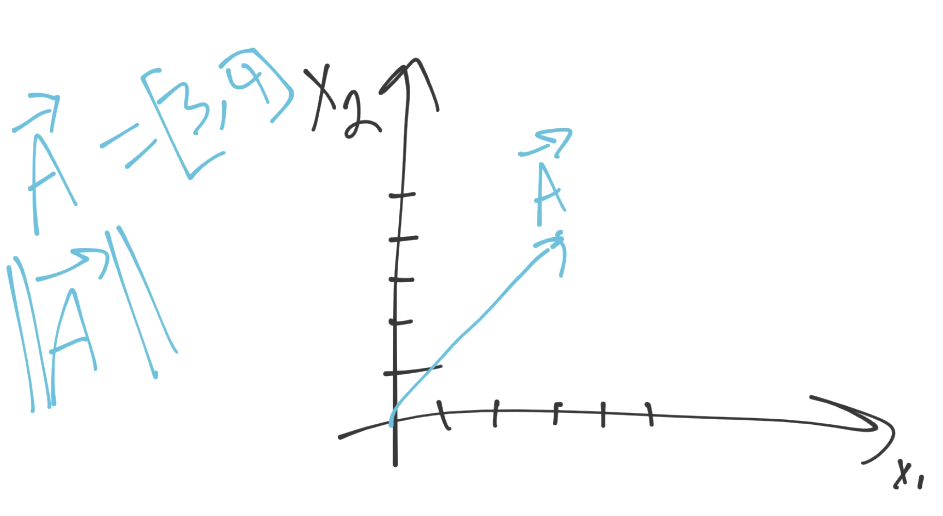
上面的例子中,向量 A(使用字母上面的箭头来表示),向[3, 4]移动。可以将每个坐标看做该维度上的方向。我们这里,有两个维度。我们在第一维里面移动 3 个单位,第二维里面移动 4 个。这就是方向了,那么模是什么呢?我们之前看到过它,它就是欧氏距离,范式,或者是大小。对我们来说,最重要的是,它们的计算方式相同(平方和的平方根)。
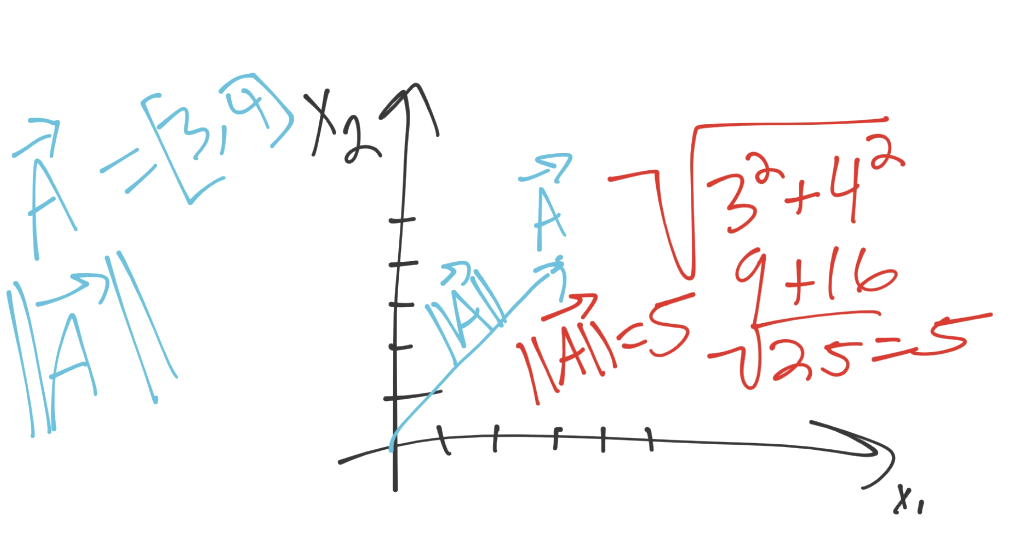
我们这里,向量的模是 5。如果你仔细观察图片,你可能会注意一些其它东西:
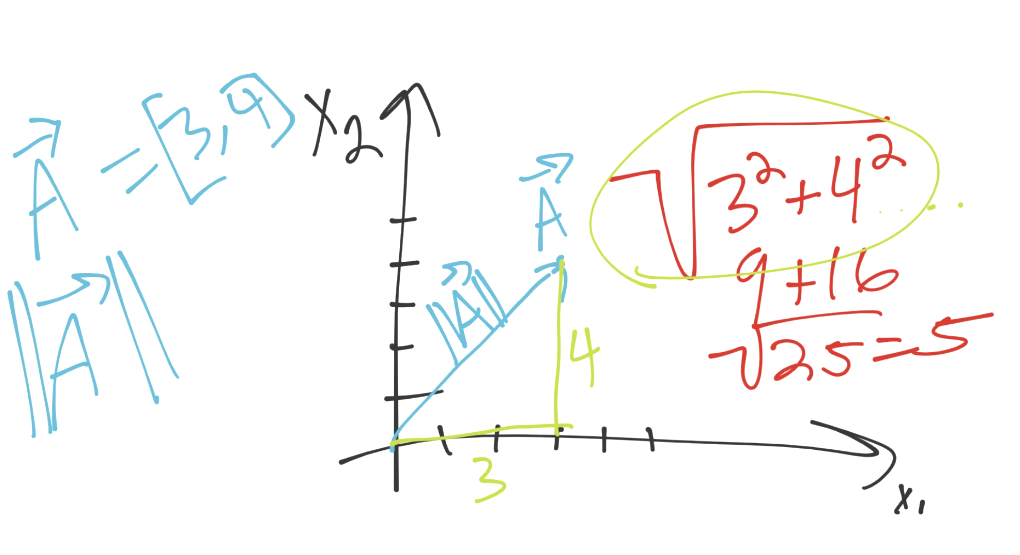
看起来像是直角三角形的勾股(帕斯卡)定理。的确是相同的公式,只要我们进入更高的维度,它就不是简单的三角形了。
很简单,下面是点积。如果我们对向量计算点积会发生什么呢?假设有两个向量,A 和 B。A 是[1, 3],B 是[4, 2]。我们所做的是,将对应分量相乘再相加。例如:
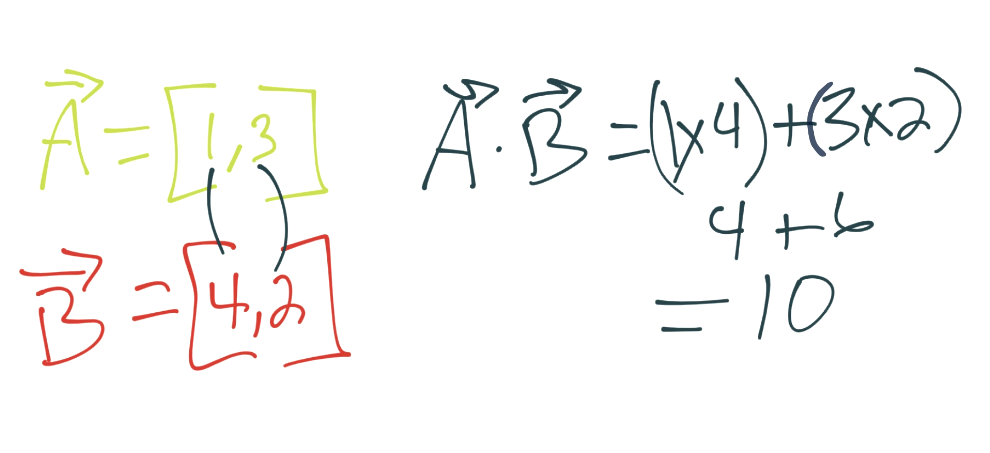
好的,既然我们知道了这些东西,我们就要讲解支持向量机本身了。我们作为科学家,首先会在机器上做一些断言。
二十二、支持向量断言
欢迎阅读机器学习教程的第二十二章。这个教程中,我们会涉及一些 SVM 的断言。理解这些断言,它们中一些是约束,是是理解 SVM 的数学与美的一部分。
首先,让我们看一看 SVM 的示例目标。它的理念是接受已知数据,之后 SVM 的拟合或者训练是个最优化问题,寻找数据的最佳分隔直线,也就是决策边界,像这样:
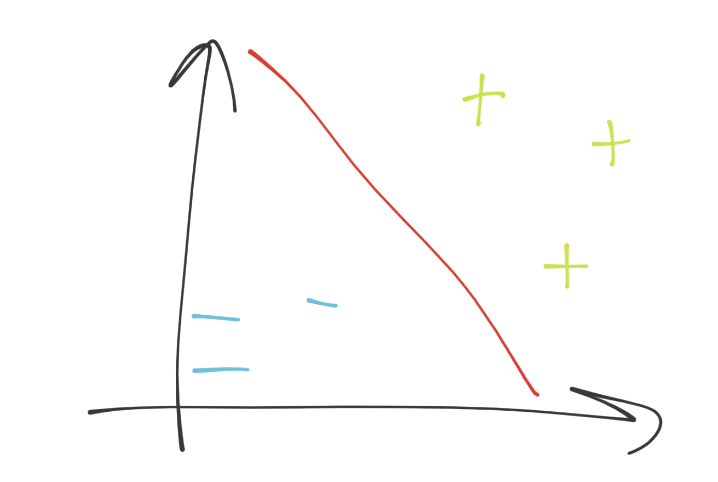
我们在二维空间中,所以分隔超平面(决策边界)也就是简单的直线(红色直线)。决策边界分隔了蓝色减号分组,和绿色加号分组。下面,如果我们在图中任意位置放一个点,我们就可以做一个简单的检查,来看看它位于分隔直线的哪一边,我们就会有答案了。是不是很简单?如果我们仅仅停留在二维空间,我们这里的维度是什么呢?每个特征都是一个维度,所有特征组成了我们的特征集。因此,我们可能拥有一条简单的直线,超级简单。我们可以使用线性代数来解决它。但如果我们拥有 63 个特征,也就是 63 维呢?
目前为止还不清楚,但是勾股定理多于二维是没问题的。好的,我们来看看向量空间吧。我们现在在向量空间中了,我们拥有了未知的特征集,记为v。之后,我们有了另一个向量(法向量),和决策边界正交,记为w。看起来是:
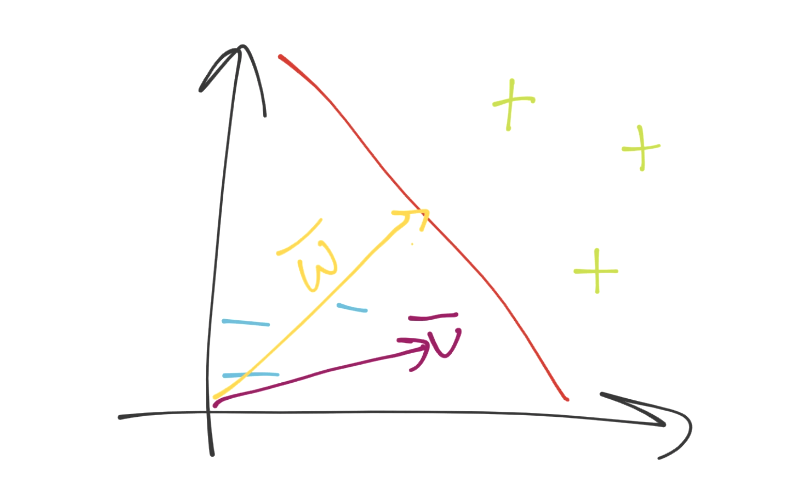
现在如何呢?我们可以用眼睛看出来,但是如何用数学表达呢?同样,要记得你需要一个方法,在 2 维和 5902 维都工作。你可以仅仅将向量v和w点乘,并加上一些偏移b(就是超平面的一般式方程),之后观察这个值大于还是小于 0。
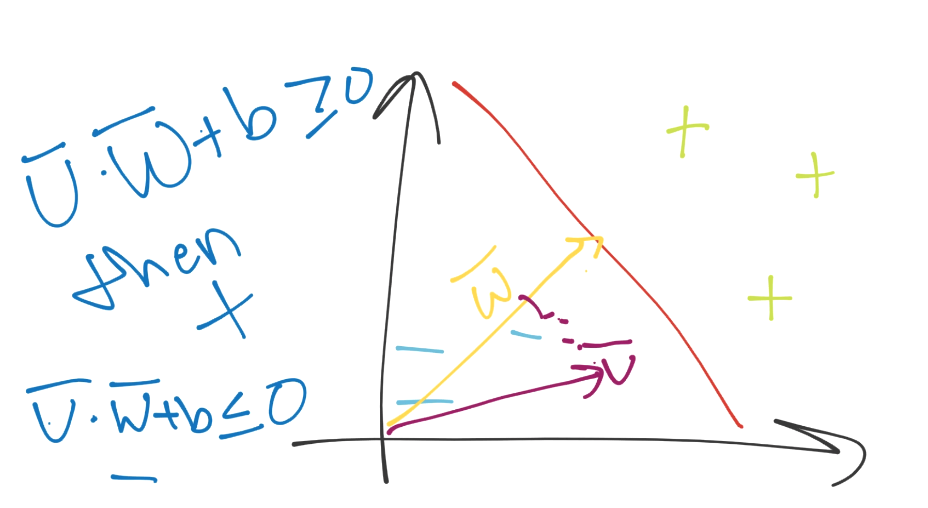
好的,尽管我们这里不知道w和b都是什么。
然后就复杂了。
我们有了两个未知变量,并且有个坏消息:我们要求解它们。根据优化来说,这应该是个危险信号,也就是有无限个w和b满足我们的方程,但是我们也知道有一种约束,已经在我们的脑子里定义了逻辑:我们想要最佳的分隔超平面。我们可以大致猜测这是w和b优化的一部分。最开始我们打算设置一些真实的数学约束。
目前为止,我们仅仅看到了分隔超平面,但是分隔超平面在两个超平面之间。所谓的支持向量经过两个超平面,这些支持向量是特征集(图上的数据点),如果移动了它们,就会对最佳分隔超平面有影响。
由于这些支持向量会产生重大影响,我们打算为其设置一个常量值。前面说,分类函数是sign(x·w + b),如果它是 0,那就说明在决策边界上。如果大于零,就是正向分类,如果小于零,就是负向分类。我们打算利用它,并且认为,如果x·w + b为 1,就是正向支持向量,如果为 -1,就是负向支持向量。如果一个未知值是 -0.52,仍然是负向分类,即使它没有超过支持向量的标记 -1。我们简单使用支持向量来帮助我们选取最佳分隔超平面,这就是它们的作用。我们的断言是:
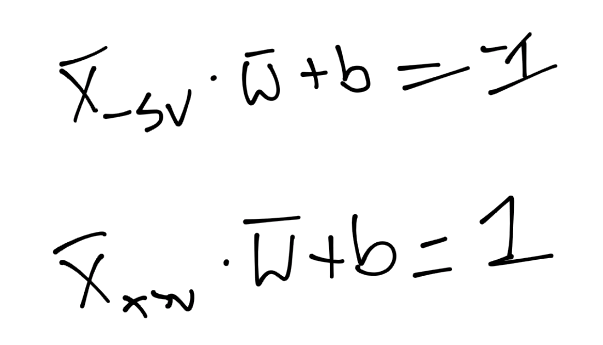
也就是说,第一行,我们让X负向支持向量(这是任何为负向支持向量的特征)点乘向量w再加b等于 -1。我们断言了这个。之后对正向支持向量:X正向支持向量点乘向量w再加b为正一。同样,我们刚开始,没有真正的证明,我们刚刚说这是一个案例。现在,我们打算引入新的值,Yi。
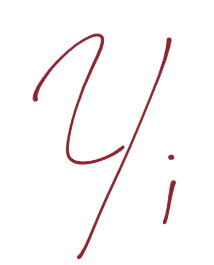
y 在 Python 代码中是我们的分类,这里也是。
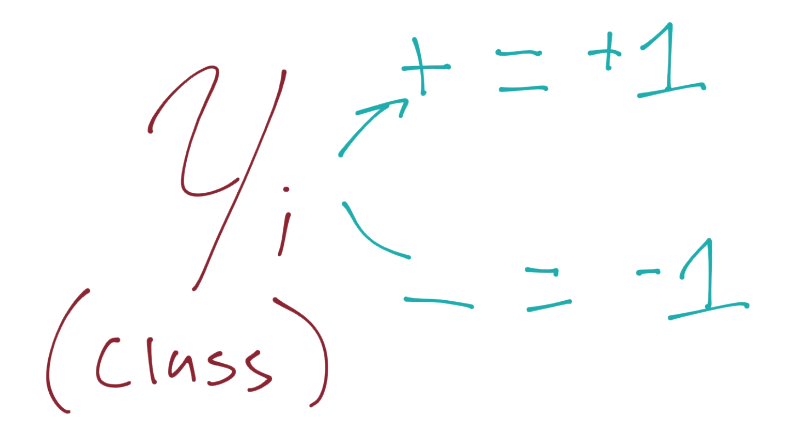
我们打算向之前的断言引入它,如果你记得正向和负向支持向量的值:x·w+b=1是正向,x·w+b=-1是负向。我们打算将我们的原始断言相乘:
根据这个新的Yi值,它同样是 -1 或者 1(取决于分类是 -1 还是 1)。当我们将原始断言相乘时,我们就需要将两边都乘Yi,也就是:

我们将Yi的符号留在左边,但是我们实际上将其应用到了右边(1 或者 -1)。这样意味着对于正向支持向量,我们得到了1x1=1,对于负向支持向量,我们得到了(-1)x(-1)=1,也等于 1。我们可以将每个方程的右边设为 0,通过两边都减一,我们就有了相同的方程Yi(Xi·w+b)-1 = 0。
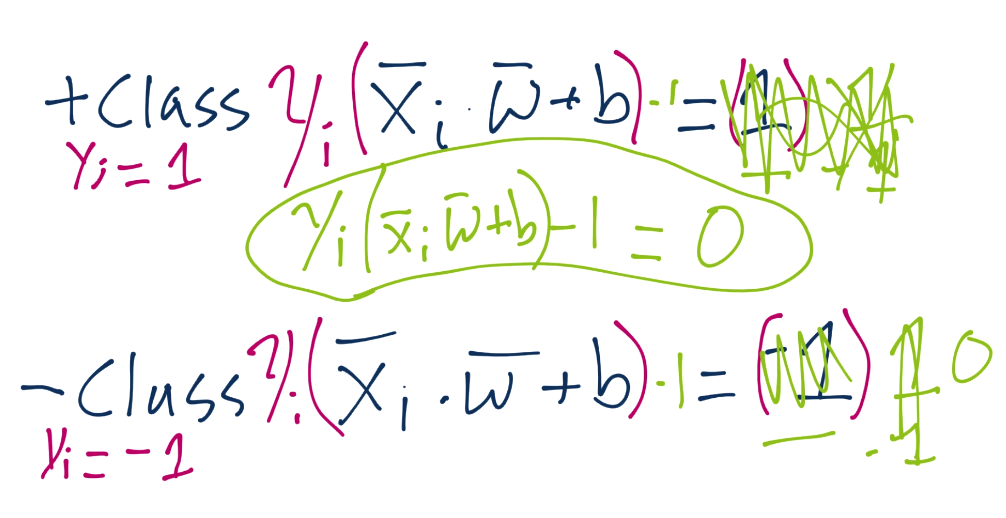
现在我们拥有了约束,下个教程中我们会深入讲解。
二十三、支持向量机基础
欢迎阅读第二十三篇教程。这篇教程中,我们打算为支持向量机的优化来解方程。
我们需要计算的支持向量为:Yi(Xi·w+b)-1 = 0。
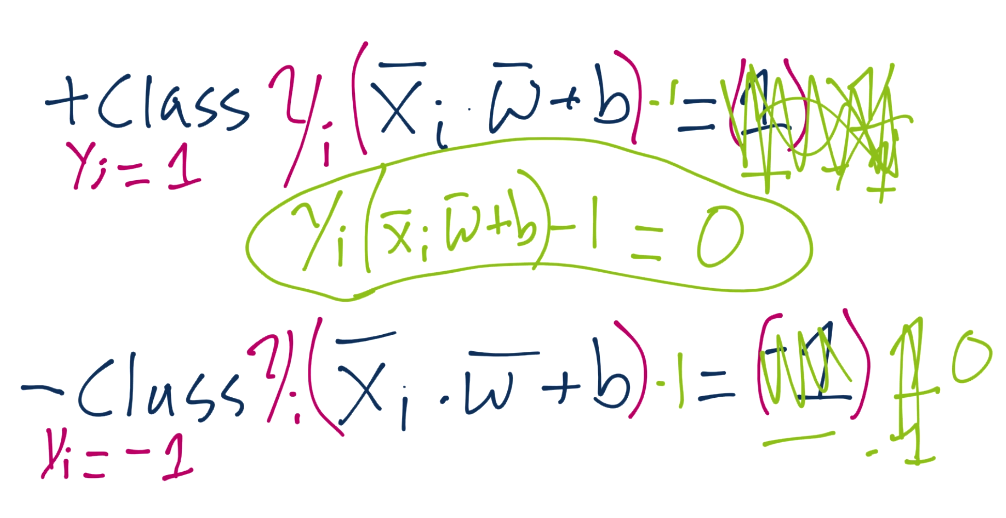
现在我们打算讨论一下,我们如何处理这个支持向量机的形式优化问题。特别是,我们如何获取向量w和b的最优解。我们也会涉及一些支持向量机的其它基础。
开始,之前说过超平面的定义为w·x+b。因此,我们断言了该方程中支持向量机的定义,正向类为 1,负向类为 -1。
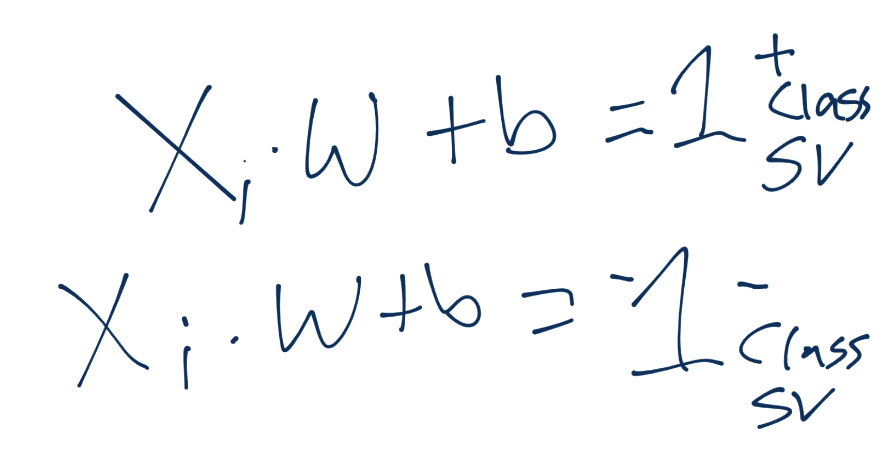
我们也推测,一旦我们找到了满足约束问题(w的模最小,b最大)的w和b,我们用于未知点的分类决策函数,只需要简单计算x·w+b。如果值为 0.99 呢?它在图中是什么样子?

所以它并不在正向支持向量平面上,但是很接近了。它超过了决策边界没有?是的,决策边界是x·w+b=0。因此,未知数据集的实际决策函数只是sign(x·w+b)。就是它了。如果它是正的,就是+分类,负的就是-分类。现在为了求得这个函数,我们需要w和b。我们的约束函数,Yi(Xi·W+b) >= 1,需要满足每个数据集。我们如何使其大于等于 1 呢?如果不乘 Yi,就仅仅需要我们的已知数据集,如果代入x·w+b大于 1 或者小于 -1,尽管我们之前提到过,0.98 的值也是正向分类。原因就是,新的或者未知的数据可以位于支持向量平面和决策边界之间,但是训练集或已知数据不可以。
于是,我们的目标就是最小化|w|,最大化b,并保持Yi(X·W+b)>=1的约束。
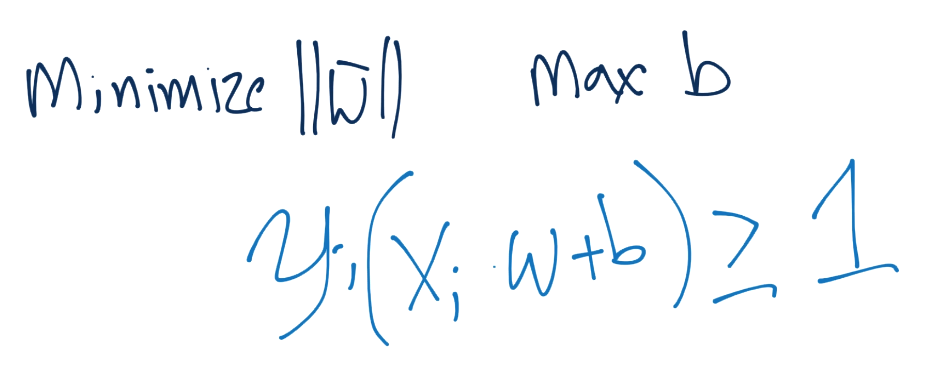
要注意,我们尝试满足向量w的约束,但是我们需要最小化w的模,而不是w,不要混淆。
有许多方式来计算这个带约束的最优化。第一个方式就是支持向量机的传统描述。开始,我们尝试将分隔超平面之间的宽度最大化。
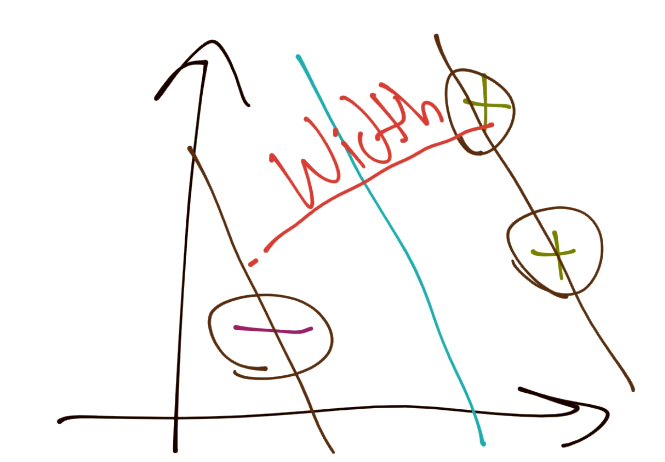
下面,向量之间的距离可以记为:
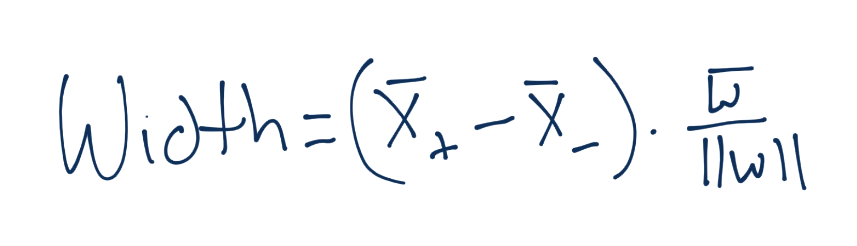
要注意,这里我们得到了X+和X-,这是两个超平面,我们尝试最大化之间的距离。幸运的是,这里没有b,非常好。那么,X+和X-又是什么呢?我们知道吗?是的,我们知道。
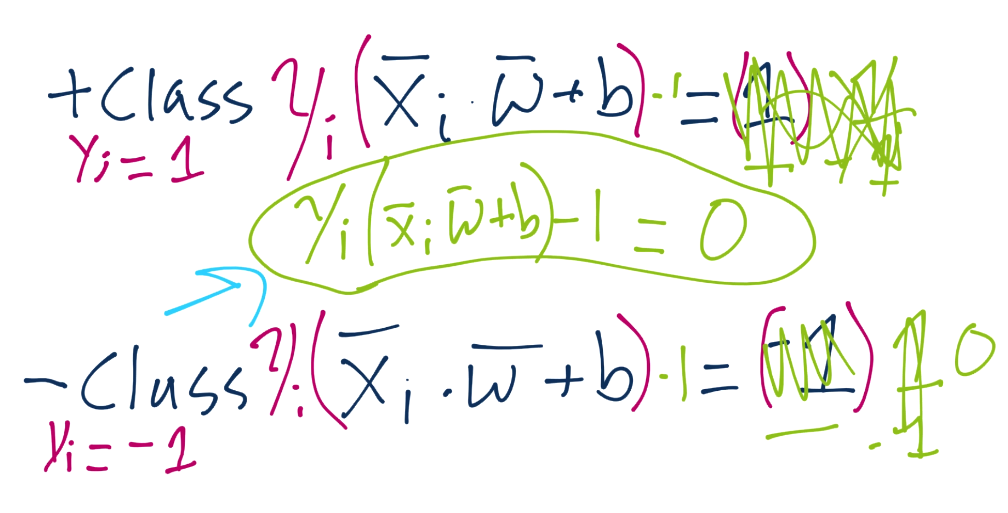
这里就有b了。总有一天我们会将其解出来。无论如何,我们做一些代数,将X+和X-替换为1-b和1+b。
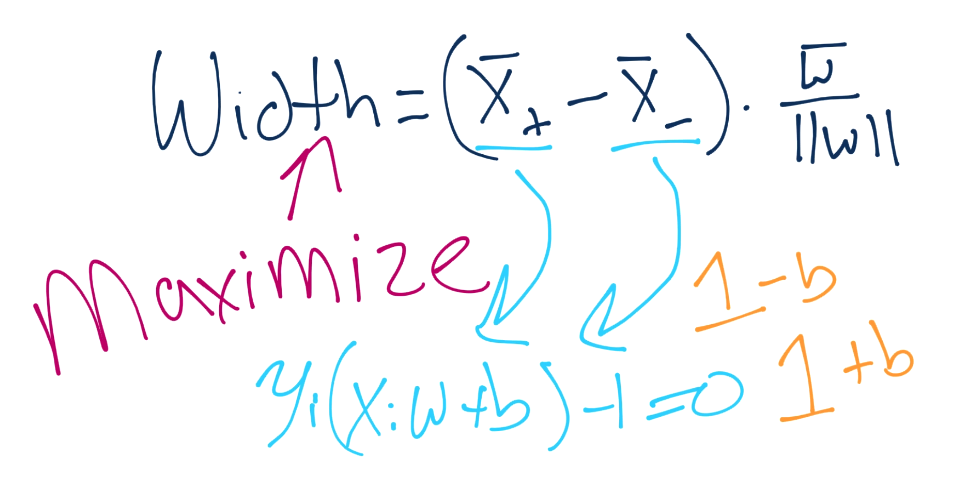
记得你的操作顺序吗?这非常方便,我们就将b移走了,现在我们的方程极大简化了。
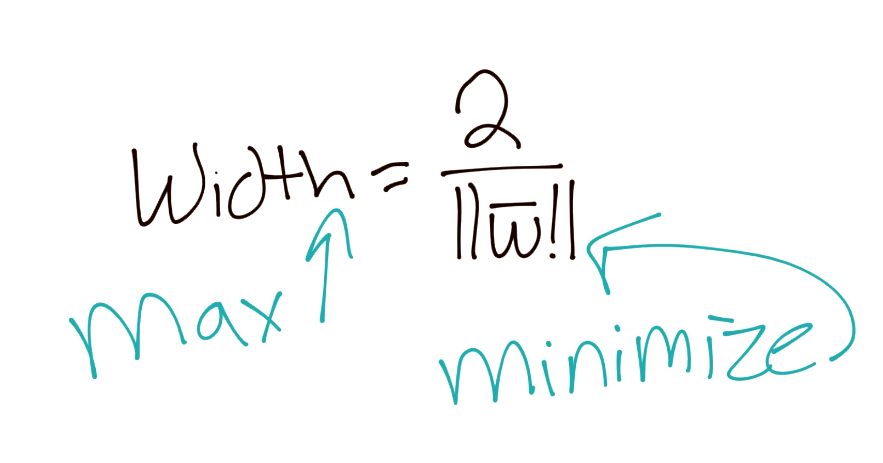
为了更好地满足我们未来的要求,我们可以认为,如果我们打算最大化2/|w|,我们就可以最小化|w|,这个之前已经讲过了。由于我们打算最小化|w|,相当于最小化1/2 * |w|^2:

我们的约束是Yi(Xi·W+b)-1 = 0。因此,所有特征集的和应该也是 0。所以我们引入了拉格朗日乘数法:
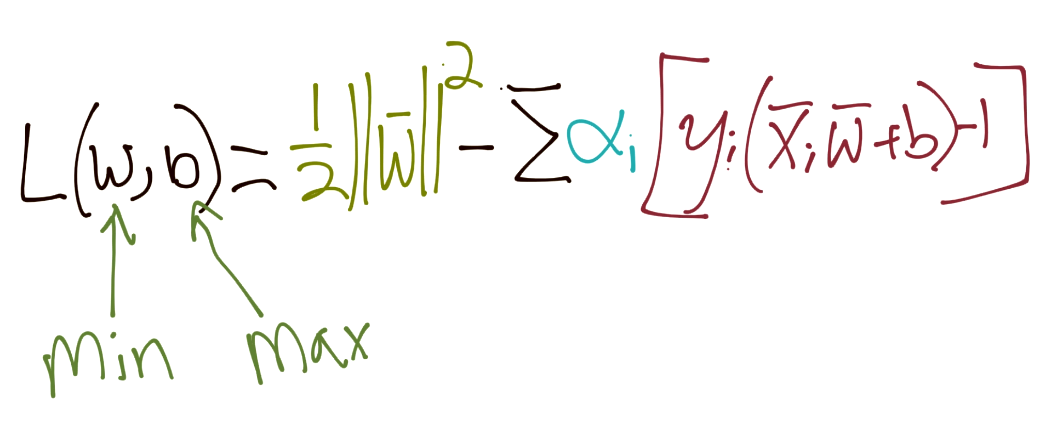
在这里求导:
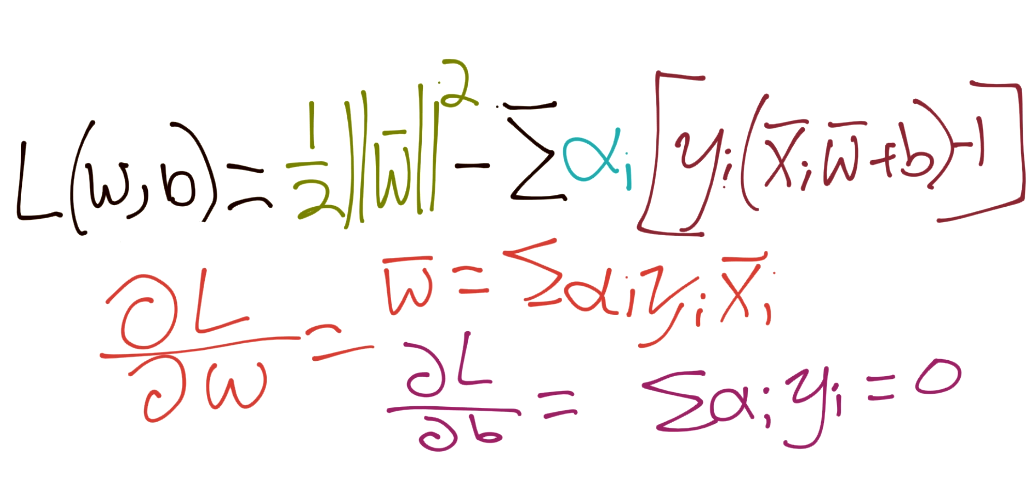
把所有东西放到一起:
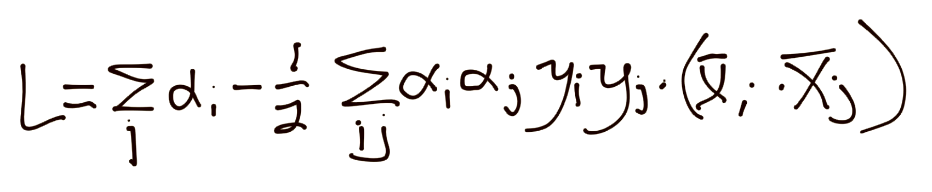
于是,如果你没有对求出来的东西不满意,你就到这里了。我们得到了alpha的平方,也就是说,我们需要解决一个平方规划。
很快就变复杂了。
下一篇教程中,我们的兴趣是从零编写 SVM,我们看看是否可以将其简化。
二十四、约束优化
欢迎阅读第二十四篇教程。这个教程中,我们打算深入讨论 SVM 的约束优化。
上一个教程中,我们剩下了 SVM 的形式约束优化问题:
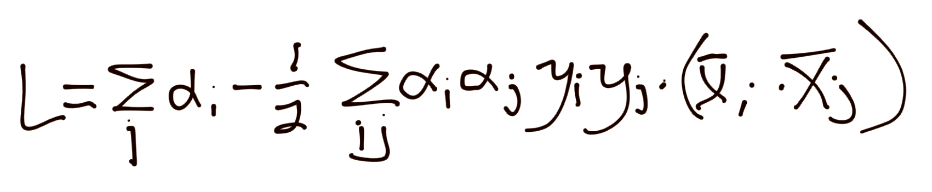
看起来很丑陋,并且由于alpha的平方,我们看到了一个平方规划问题,这不是很容易完成。约束优化不是一个很大的范围吗?有没有别的方式?你怎么问我会很高兴,因为是的,的确存在其他方式。SVM 的优化问题是个凸优化问题,其中凸优化的形状是w的模。

这个凸优化的目标是寻找w的最大模。一种解决凸优化问题的方式就是“下降”,直到你不能再往下走了。一旦你到达了底部,你就能通过其他路径慢慢回去,重复这个步骤,直到你到达了真正的底部。将凸优化问题看做一个碗,求解过程就是沿着碗的边缘扔进去一个球。球会很快滚下边缘,正好达到最中间的位置,之后可能会在另一侧上升,但是会再次下降,沿着另一个路径,可能会重复几次,每次都会移动得更慢,并且距离更短,最终,球会落在碗的底部。
我们会使用 Python 来模拟这个十分相同的问题。我们会专注于向量w,以一个很大的模来开始。之前提到过向量的模就是分量的平方和的平方根。也就是说,向量w为[5,5]或者[-5,5]的模都一样。但是和特征集的点积有很大不同,并且是完全不同的超平面。出于这个原因,我们需要检查每个向量的每个变种。
我们的基本思想就是像一个球那样,快速沿侧壁下降,重复知道我们不能再下降了。这个时候,我们需要重复我们的最后几个步骤。我们以更小的步骤来执行。之后可能将这个步骤重复几次,例如:

首先,我们最开始就像绿色的线,我们用大的步长下降。我们会绕过中心,之后用更小的步长,就像红色的线。之后我们会像蓝色的线。这个方式,我们的步长会越来越小(每一步我们都会计算新的向量w和b)。这样,我们就可以获取最优化的向量w,而不需要一开始就使用较大的步长来完成相同结果,并且在处理时浪费很多时间。
如果我们找到了碗或者凸形状的底部,我们就说我们找到了全局最小值。凸优化问题非常好的原因,就是我们可以使用这个迭代方式来找到底部。如果不是凸优化,我们的形状就是这样:

现在,当从左侧开始时,你可能检测到上升了,所以你返回并找到了局部最小值。

再说一遍,我们在处理一个很好的凸优化问题,所以我们不需要担心错误。我的计划就是给定一个向量,缓慢减小向量的模(也就是讲笑向量中数据的绝对值)。对于每个向量,假设是[10, 10],我们会使用这些东西来变换向量:[1,1],[-1,1],[-1,-1],[1,-1]。这会向我们提供这个向量的所有变种,我们需要检查它们,尽管它们拥有相同的模。这就是下个教程中要做的事情。
二十五、使用 Python 从零开始编写 SVM
欢迎阅读第 25 篇教程,下面就是我们的 SVM 部分了。这个教程中,我们打算从零编写 SVM。
在深入之前,我们会专注于一些选项,用于解决约束优化问题。
首先,约束优化的话题很多,也有很多材料。即使是我们的子话题:凸优化,也是很庞大的。一个不错的起始点是 https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf。对于约束优化,你可以查看 http://www.mit.edu/~dimitrib/Constrained-Opt.pdf。
特别是在 Python 中,CVXOPT 包拥有多种凸优化方法,其中之一就是我们的平方规划问题(cvxopt.solvers.qp)。
同样,也有 libsvm 的 Python 接口,或者 libsvm 包。我们选择不要用这些东西,因为 SVM 的最优化问题几乎就是 SVM 问题的全部了。
现在,为了使用 Python 来开始写 SVM,我们以这些导入来开始。
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
我们使用 Matplotlib 来绘图,NumPy 来处理数组。下面我们会拥有一些起始数据:
data_dict = {-1:np.array([[1,7],
[2,8],
[3,8],]),
1:np.array([[5,1],
[6,-1],
[7,3],])}
现在我们打算开始构建我们的 SVM 类。如果你不熟悉面向对象编程,不要害怕。我们这里的例子是个非常基本的 OOP 形式。只要知道 OOP 创建带有对象,类中带有属性、函数(实际上是方法),以及我们使用self变量来代表对象本身。解释再多也没有意义,已经足以开始了。如果你对代码感到疑惑,可以去在线社区提问。
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
类的__init__方法是使用类创建对象时,执行的方法。其它方法只在调用时执行。对于每个方法,我们传入self作为第一个参数,主要是一种约定。下面,我们添加可视化参数。我们想看看 SVM,所以将其设为True。下面米可以看见一些变量,例如self.color和self.visualization。这样做能够让我们在类的其它方法中,引用self.color,最后,如果我们开启了可视化,我们打算绘制我们的图像。
下面,让我们继续并体感家更多方法:fit和predict。
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
# train
def fit(self, data):
pass
def predict(self,features):
# sign( x.w+b )
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
return classification
fit方法会用于训练我们的 SVM。这就是最优化的步骤。一旦我们完成了训练,predict方法会预测新特征集的值,一旦我们知道了w和b,它就是sign(x·w+b)。
目前为止的代码。
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
# train
def fit(self, data):
pass
def predict(self,features):
# sign( x.w+b )
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
return classification
data_dict = {-1:np.array([[1,7],
[2,8],
[3,8],]),
1:np.array([[5,1],
[6,-1],
[7,3],])}
下个教程中,我们会继续并开始处理fit方法。
二十六、支持向量机优化
欢迎阅读第二十六篇教程,下面就是我们的支持向量机章节。这篇教程中,我们打算处理 SVM 的优化方法fit。
目前为止的代码为:
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
# train
def fit(self, data):
pass
def predict(self,features):
# sign( x.w+b )
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
return classification
data_dict = {-1:np.array([[1,7],
[2,8],
[3,8],]),
1:np.array([[5,1],
[6,-1],
[7,3],])}
我们开始填充fit方法:
def fit(self, data):
self.data = data
# { ||w||: [w,b] }
opt_dict = {}
transforms = [[1,1],
[-1,1],
[-1,-1],
[1,-1]]
要注意这个方法首先传递self(记住这是方法的约定),之后传递data。data就是我们我们打算训练或者优化的数据。我们这里,它是data_dict,我们已经创建好了。
我们将self.data设为该数据。现在,我们可以在类中的任何地方引用这个训练数据了(但是,我们需要首先使用数据来调用这个训练方法,来避免错误)。
下面,我们开始构建最优化字典opt_dict,它包含任何最优化的值。随着我们减小我们的w向量,我们会使用约束函数来测试向量,如果存在的话,寻找最大的满足方程的b,之后将所有数据储存在我们的最华友字典中。字典是{ ||w|| : [w,b] }。当我们完成所有优化时,我们会选择字典中键最小的w和b值。
最后,我们会设置我们的转换。我们已经解释了我们的意图,来确保我们检查了每个可能的向量版本。
下面,我们需要一些匹配数据的起始点。为此,我们打算首先引用我们的训练数据,来选取一些合适的起始值。
# finding values to work with for our ranges.
all_data = []
for yi in self.data:
for featureset in self.data[yi]:
for feature in featureset:
all_data.append(feature)
self.max_feature_value = max(all_data)
self.min_feature_value = min(all_data)
# no need to keep this memory.
all_data=None
我们所做的就是遍历所有数据,寻找最大值和最小值。现在我们打算定义我们的步长。
step_sizes = [self.max_feature_value * 0.1,
self.max_feature_value * 0.01,
# starts getting very high cost after this.
self.max_feature_value * 0.001]
这里我们设置了一些大小的步长,我们打算这样执行。对于我们的第一遍,我们会采取大跨步(10%)。一旦我们使用这些步长找到了最小值,我们就将步长降至 1% 来调优。我们会继续下降,取决于你想要多么精确。我会在这个项目的末尾讨论,如何在程序中判断是否应该继续优化。
下面,我们打算设置一些变量,来帮助我们给b生成步长(用于生成比w更大的步长,因为我们更在意w的精确度),并跟踪最后一个最优值。
# extremely expensive
b_range_multiple = 5
b_multiple = 5
latest_optimum = self.max_feature_value*10
现在我们开始了:
for step in step_sizes:
w = np.array([latest_optimum,latest_optimum])
# we can do this because convex
optimized = False
while not optimized:
pass
这里的思想就是沿着向量下降。开始,我们将optimized设为False,并为我们会在每个主要步骤重置它。optimized变量再我们检查所有步骤和凸形状(我们的碗)的底部之后,会设为True。
我们下个教程中会继续实现这个逻辑,那里我们会实际使用约束问题来检查值,检查我们是否找到了可以保存的值。
目前为止的代码:
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
# train
def fit(self, data):
self.data = data
# { ||w||: [w,b] }
opt_dict = {}
transforms = [[1,1],
[-1,1],
[-1,-1],
[1,-1]]
all_data = []
for yi in self.data:
for featureset in self.data[yi]:
for feature in featureset:
all_data.append(feature)
self.max_feature_value = max(all_data)
self.min_feature_value = min(all_data)
all_data = None
step_sizes = [self.max_feature_value * 0.1,
self.max_feature_value * 0.01,
# point of expense:
self.max_feature_value * 0.001,]
# extremely expensive
b_range_multiple = 5
#
b_multiple = 5
latest_optimum = self.max_feature_value*10
for step in step_sizes:
w = np.array([latest_optimum,latest_optimum])
# we can do this because convex
optimized = False
while not optimized:
pass
def predict(self,features):
# sign( x.w+b )
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
return classification
data_dict = {-1:np.array([[1,7],
[2,8],
[3,8],]),
1:np.array([[5,1],
[6,-1],
[7,3],])}
二十七、支持向量机优化 第二部分
欢迎阅读第二十七篇教程,下面就是支持向量机的部分。这个教程中,我们打算继续使用 Python 代码处理 SVM 优化问题。
在我们停止的地方,我们的代码为:
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
# train
def fit(self, data):
self.data = data
# { ||w||: [w,b] }
opt_dict = {}
transforms = [[1,1],
[-1,1],
[-1,-1],
[1,-1]]
all_data = []
for yi in self.data:
for featureset in self.data[yi]:
for feature in featureset:
all_data.append(feature)
self.max_feature_value = max(all_data)
self.min_feature_value = min(all_data)
all_data = None
step_sizes = [self.max_feature_value * 0.1,
self.max_feature_value * 0.01,
# point of expense:
self.max_feature_value * 0.001,]
# extremely expensive
b_range_multiple = 5
#
b_multiple = 5
latest_optimum = self.max_feature_value*10
for step in step_sizes:
w = np.array([latest_optimum,latest_optimum])
# we can do this because convex
optimized = False
while not optimized:
pass
def predict(self,features):
# sign( x.w+b )
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
return classification
data_dict = {-1:np.array([[1,7],
[2,8],
[3,8],]),
1:np.array([[5,1],
[6,-1],
[7,3],])}
选取while not optimized部分:
optimized = False
while not optimized:
for b in np.arange(-1*(self.max_feature_value*b_range_multiple),
self.max_feature_value*b_range_multiple,
step*b_multiple):
这里我们开始迭代所有可能的b值,并且现在可以看到,之前设置的b值。这里要注意,我们使用一个固定的步长,直接迭代b。我们也可以拆分b的步长,就像我们对w所做的那样。为了使事情更加准确,你可能打算这样实现。也就是说,出于简洁,我打算跳过这个部分,因为我们要完成近似的结果。而不是尝试获得什么奖项。
继续:
optimized = False
while not optimized:
for b in np.arange(-1*(self.max_feature_value*b_range_multiple),
self.max_feature_value*b_range_multiple,
step*b_multiple):
for transformation in transforms:
w_t = w*transformation
found_option = True
# weakest link in the SVM fundamentally
# SMO attempts to fix this a bit
# yi(xi.w+b) >= 1
#
# #### add a break here later..
for i in self.data:
for xi in self.data[i]:
yi=i
if not yi*(np.dot(w_t,xi)+b) >= 1:
found_option = False
if found_option:
opt_dict[np.linalg.norm(w_t)] = [w_t,b]
现在我们迭代了每个变形,对我们的约束条件测试了每个东西。如果我们数据集中的任何特征集不满足我们的约束,我们就会去掉这个变量,因为它不匹配,并继续。我建议在这里停顿一下。如果仅仅是一个变量不工作,你可能要放弃其余部分,因为一个变量不匹配,就足以扔掉w和b了。你应该在这里停顿,并且处理循环。现在,我们会将代码保持原样,但是我在录制视频的时候,会有所修改。
现在我们完成fit方法,我会贴出完整代码并解释差异:
def fit(self, data):
self.data = data
# { ||w||: [w,b] }
opt_dict = {}
transforms = [[1,1],
[-1,1],
[-1,-1],
[1,-1]]
all_data = []
for yi in self.data:
for featureset in self.data[yi]:
for feature in featureset:
all_data.append(feature)
self.max_feature_value = max(all_data)
self.min_feature_value = min(all_data)
all_data = None
# support vectors yi(xi.w+b) = 1
step_sizes = [self.max_feature_value * 0.1,
self.max_feature_value * 0.01,
# point of expense:
self.max_feature_value * 0.001,]
# extremely expensive
b_range_multiple = 5
# we dont need to take as small of steps
# with b as we do w
b_multiple = 5
latest_optimum = self.max_feature_value*10
for step in step_sizes:
w = np.array([latest_optimum,latest_optimum])
# we can do this because convex
optimized = False
while not optimized:
for b in np.arange(-1*(self.max_feature_value*b_range_multiple),
self.max_feature_value*b_range_multiple,
step*b_multiple):
for transformation in transforms:
w_t = w*transformation
found_option = True
# weakest link in the SVM fundamentally
# SMO attempts to fix this a bit
# yi(xi.w+b) >= 1
#
# #### add a break here later..
for i in self.data:
for xi in self.data[i]:
yi=i
if not yi*(np.dot(w_t,xi)+b) >= 1:
found_option = False
if found_option:
opt_dict[np.linalg.norm(w_t)] = [w_t,b]
if w[0] < 0:
optimized = True
print('Optimized a step.')
else:
w = w - step
norms = sorted([n for n in opt_dict])
#||w|| : [w,b]
opt_choice = opt_dict[norms[0]]
self.w = opt_choice[0]
self.b = opt_choice[1]
latest_optimum = opt_choice[0][0]+step*2
一旦我们越过了w向量的零点,就没有理由继续了,因为我们通过变换测试了负值。所以我们已经完成了这个步长,要么继续下一个步长,要么就完全完成了。如果没有经过 0,那就向下走一步。一旦我们走完了能走的所有步骤,我们就对opt_dict字典的键数组记性排序(它包含||w|| : [w,b])。我们想要向量w的最小模,所以我们选取列表的第一个元素。我们给这里的self.w和self.b赋值,并设置最后的优化值。之后,我们选取另一个步长,或者完全完成了整个过程(如果没有更多的步长可选取了)。
这里,完整代码是:
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
# train
def fit(self, data):
self.data = data
# { ||w||: [w,b] }
opt_dict = {}
transforms = [[1,1],
[-1,1],
[-1,-1],
[1,-1]]
all_data = []
for yi in self.data:
for featureset in self.data[yi]:
for feature in featureset:
all_data.append(feature)
self.max_feature_value = max(all_data)
self.min_feature_value = min(all_data)
all_data = None
# support vectors yi(xi.w+b) = 1
step_sizes = [self.max_feature_value * 0.1,
self.max_feature_value * 0.01,
# point of expense:
self.max_feature_value * 0.001,]
# extremely expensive
b_range_multiple = 5
# we dont need to take as small of steps
# with b as we do w
b_multiple = 5
latest_optimum = self.max_feature_value*10
for step in step_sizes:
w = np.array([latest_optimum,latest_optimum])
# we can do this because convex
optimized = False
while not optimized:
for b in np.arange(-1*(self.max_feature_value*b_range_multiple),
self.max_feature_value*b_range_multiple,
step*b_multiple):
for transformation in transforms:
w_t = w*transformation
found_option = True
# weakest link in the SVM fundamentally
# SMO attempts to fix this a bit
# yi(xi.w+b) >= 1
#
# #### add a break here later..
for i in self.data:
for xi in self.data[i]:
yi=i
if not yi*(np.dot(w_t,xi)+b) >= 1:
found_option = False
if found_option:
opt_dict[np.linalg.norm(w_t)] = [w_t,b]
if w[0] < 0:
optimized = True
print('Optimized a step.')
else:
w = w - step
norms = sorted([n for n in opt_dict])
#||w|| : [w,b]
opt_choice = opt_dict[norms[0]]
self.w = opt_choice[0]
self.b = opt_choice[1]
latest_optimum = opt_choice[0][0]+step*2
def predict(self,features):
# sign( x.w+b )
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
return classification
data_dict = {-1:np.array([[1,7],
[2,8],
[3,8],]),
1:np.array([[5,1],
[6,-1],
[7,3],])}
现在我们已经准备好可视化以及测试支持向量机的预测了。我们会在下一个教程中完成它们。
二十八、使用我们的 SVM 来可视化和预测
欢迎阅读第二十八篇教程。这个教程中,我们完成我们从零开始的基本 SVM,并使用它来可视化并作出预测。
我们目前为止的代码:
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
# train
def fit(self, data):
self.data = data
# { ||w||: [w,b] }
opt_dict = {}
transforms = [[1,1],
[-1,1],
[-1,-1],
[1,-1]]
all_data = []
for yi in self.data:
for featureset in self.data[yi]:
for feature in featureset:
all_data.append(feature)
self.max_feature_value = max(all_data)
self.min_feature_value = min(all_data)
all_data = None
# support vectors yi(xi.w+b) = 1
step_sizes = [self.max_feature_value * 0.1,
self.max_feature_value * 0.01,
# point of expense:
self.max_feature_value * 0.001,]
# extremely expensive
b_range_multiple = 5
# we dont need to take as small of steps
# with b as we do w
b_multiple = 5
latest_optimum = self.max_feature_value*10
for step in step_sizes:
w = np.array([latest_optimum,latest_optimum])
# we can do this because convex
optimized = False
while not optimized:
for b in np.arange(-1*(self.max_feature_value*b_range_multiple),
self.max_feature_value*b_range_multiple,
step*b_multiple):
for transformation in transforms:
w_t = w*transformation
found_option = True
# weakest link in the SVM fundamentally
# SMO attempts to fix this a bit
# yi(xi.w+b) >= 1
#
# #### add a break here later..
for i in self.data:
for xi in self.data[i]:
yi=i
if not yi*(np.dot(w_t,xi)+b) >= 1:
found_option = False
if found_option:
opt_dict[np.linalg.norm(w_t)] = [w_t,b]
if w[0] < 0:
optimized = True
print('Optimized a step.')
else:
w = w - step
norms = sorted([n for n in opt_dict])
#||w|| : [w,b]
opt_choice = opt_dict[norms[0]]
self.w = opt_choice[0]
self.b = opt_choice[1]
latest_optimum = opt_choice[0][0]+step*2
def predict(self,features):
# sign( x.w+b )
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
return classification
data_dict = {-1:np.array([[1,7],
[2,8],
[3,8],]),
1:np.array([[5,1],
[6,-1],
[7,3],])}
我们已经拥有预测方法了,因为这非常简单。但是现在我们打算添加一些,来处理预测的可视化。
def predict(self,features):
# classifiction is just:
# sign(xi.w+b)
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
# if the classification isn't zero, and we have visualization on, we graph
if classification != 0 and self.visualization:
self.ax.scatter(features[0],features[1],s=200,marker='*', c=self.colors[classification])
else:
print('featureset',features,'is on the decision boundary')
return classification
上面,我们添加了代码来可视化预测,如果存在的话。我们打算一次做一个,但是你可以扩展代码来一次做许多个,就像 Sklearn 那样。
下面,让我们构建visualize方法:
def visualize(self):
#scattering known featuresets.
[[self.ax.scatter(x[0],x[1],s=100,color=self.colors[i]) for x in data_dict[i]] for i in data_dict]
这一行所做的就是,遍历我们的数据,并绘制它和它的相应颜色。
下面,我们打算绘制正向和负向支持向量的超平面,以及决策边界。为此,我们至少需要两个点,来创建“直线”,它就是我们的超平面。
一旦我们知道了w和b,我们就可以使用代数来创建函数,它对x值返回y值来生成直线:
def hyperplane(x,w,b,v):
# w[0] * x + w[1] * y + b = v
# 正向支持超平面 v = 1
# 最佳分隔超平面 v = 0
# 负向支持超平面 v = -1
# y = (v - b - w[0] * x) / w[1]
return (-w[0]*x-b+v) / w[1]
然后,我们创建一些变量,来存放我们打算引用的多种数据:
datarange = (self.min_feature_value*0.9,self.max_feature_value*1.1)
hyp_x_min = datarange[0]
hyp_x_max = datarange[1]
我们的主要目标就是弄清楚为了绘制我们的超平面,我们需要什么值。
现在,让我们绘制正向支持向量超平面。
# w.x + b = 1
# pos sv hyperplane
psv1 = hyperplane(hyp_x_min, self.w, self.b, 1)
psv2 = hyperplane(hyp_x_max, self.w, self.b, 1)
self.ax.plot([hyp_x_min,hyp_x_max], [psv1,psv2], "k")
非常简单,我们获得了x_min和x_max的y值,然后我们绘制了它们。
···
# w.x + b = -1
# negative sv hyperplane
nsv1 = hyperplane(hyp_x_min, self.w, self.b, -1)
nsv2 = hyperplane(hyp_x_max, self.w, self.b, -1)
self.ax.plot([hyp_x_min,hyp_x_max], [nsv1,nsv2], "k")
# w.x + b = 0
# decision
db1 = hyperplane(hyp_x_min, self.w, self.b, 0)
db2 = hyperplane(hyp_x_max, self.w, self.b, 0)
self.ax.plot([hyp_x_min,hyp_x_max], [db1,db2], "g--")
plt.show()
现在,在底部添加一些代码来训练、预测和可视化:
```py
import matplotlib.pyplot as plt
from matplotlib import style
import numpy as np
style.use('ggplot')
class Support_Vector_Machine:
def __init__(self, visualization=True):
self.visualization = visualization
self.colors = {1:'r',-1:'b'}
if self.visualization:
self.fig = plt.figure()
self.ax = self.fig.add_subplot(1,1,1)
# train
def fit(self, data):
self.data = data
# { ||w||: [w,b] }
opt_dict = {}
transforms = [[1,1],
[-1,1],
[-1,-1],
[1,-1]]
all_data = []
for yi in self.data:
for featureset in self.data[yi]:
for feature in featureset:
all_data.append(feature)
self.max_feature_value = max(all_data)
self.min_feature_value = min(all_data)
all_data = None
# support vectors yi(xi.w+b) = 1
step_sizes = [self.max_feature_value * 0.1,
self.max_feature_value * 0.01,
# point of expense:
self.max_feature_value * 0.001,
]
# extremely expensive
b_range_multiple = 2
# we dont need to take as small of steps
# with b as we do w
b_multiple = 5
latest_optimum = self.max_feature_value*10
for step in step_sizes:
w = np.array([latest_optimum,latest_optimum])
# we can do this because convex
optimized = False
while not optimized:
for b in np.arange(-1*(self.max_feature_value*b_range_multiple),
self.max_feature_value*b_range_multiple,
step*b_multiple):
for transformation in transforms:
w_t = w*transformation
found_option = True
# weakest link in the SVM fundamentally
# SMO attempts to fix this a bit
# yi(xi.w+b) >= 1
#
# #### add a break here later..
for i in self.data:
for xi in self.data[i]:
yi=i
if not yi*(np.dot(w_t,xi)+b) >= 1:
found_option = False
#print(xi,':',yi*(np.dot(w_t,xi)+b))
if found_option:
opt_dict[np.linalg.norm(w_t)] = [w_t,b]
if w[0] < 0:
optimized = True
print('Optimized a step.')
else:
w = w - step
norms = sorted([n for n in opt_dict])
#||w|| : [w,b]
opt_choice = opt_dict[norms[0]]
self.w = opt_choice[0]
self.b = opt_choice[1]
latest_optimum = opt_choice[0][0]+step*2
for i in self.data:
for xi in self.data[i]:
yi=i
print(xi,':',yi*(np.dot(self.w,xi)+self.b))
def predict(self,features):
# sign( x.w+b )
classification = np.sign(np.dot(np.array(features),self.w)+self.b)
if classification !=0 and self.visualization:
self.ax.scatter(features[0], features[1], s=200, marker='*', c=self.colors[classification])
return classification
def visualize(self):
[[self.ax.scatter(x[0],x[1],s=100,color=self.colors[i]) for x in data_dict[i]] for i in data_dict]
# hyperplane = x.w+b
# v = x.w+b
# psv = 1
# nsv = -1
# dec = 0
def hyperplane(x,w,b,v):
return (-w[0]*x-b+v) / w[1]
datarange = (self.min_feature_value*0.9,self.max_feature_value*1.1)
hyp_x_min = datarange[0]
hyp_x_max = datarange[1]
# (w.x+b) = 1
# positive support vector hyperplane
psv1 = hyperplane(hyp_x_min, self.w, self.b, 1)
psv2 = hyperplane(hyp_x_max, self.w, self.b, 1)
self.ax.plot([hyp_x_min,hyp_x_max],[psv1,psv2], 'k')
# (w.x+b) = -1
# negative support vector hyperplane
nsv1 = hyperplane(hyp_x_min, self.w, self.b, -1)
nsv2 = hyperplane(hyp_x_max, self.w, self.b, -1)
self.ax.plot([hyp_x_min,hyp_x_max],[nsv1,nsv2], 'k')
# (w.x+b) = 0
# positive support vector hyperplane
db1 = hyperplane(hyp_x_min, self.w, self.b, 0)
db2 = hyperplane(hyp_x_max, self.w, self.b, 0)
self.ax.plot([hyp_x_min,hyp_x_max],[db1,db2], 'y--')
plt.show()
data_dict = {-1:np.array([[1,7],
[2,8],
[3,8],]),
1:np.array([[5,1],
[6,-1],
[7,3],])}
svm = Support_Vector_Machine()
svm.fit(data=data_dict)
predict_us = [[0,10],
[1,3],
[3,4],
[3,5],
[5,5],
[5,6],
[6,-5],
[5,8]]
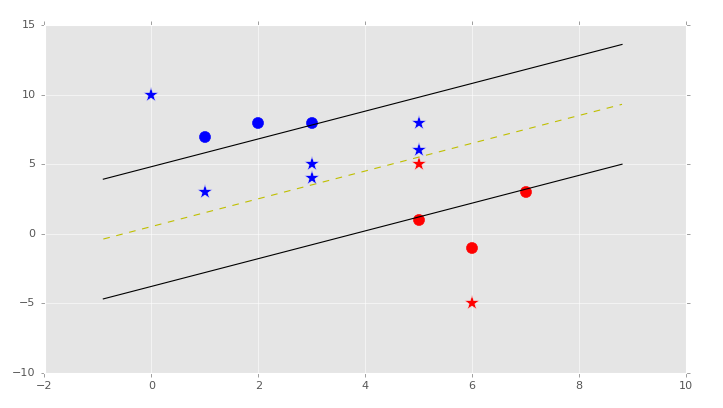
for p in predict_us:
svm.predict(p)
svm.visualize()
我们的结果:
二十九、核的简介
欢迎阅读第二十九篇教程。这个教程中,我们打算使用机器学习谈论核的概念。
回忆一开始的 SVM 话题,我们的问题是,你可不可以使用 SVM 来处理这样的数据:
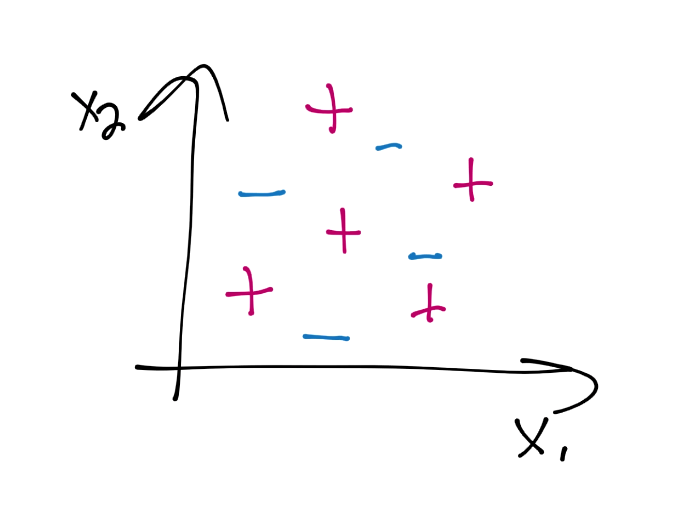
至少我们现在为止,它可能吗?不,完全不可能,至少不能是这样。但是一个选择,就是采取新的视角。我们可以通过添加一个新的维度来实现。例如上面的数据中,我们可以添加第三个维度,使用一些函数,比如X3 = X1*X2。在这里可能管用,但是也可以不管用。同样,一些案例,比如图像分析又如何呢?其中你可能有多于几百和维度。它就是性能很重要的场景,并且你是否应该添加一个维度到已经有很多维度的数据中,我们会进一步把事情变慢。
如果我告诉你,你可以在无限的维度上做计算,或者,你可以让那些计算在这些维度上实现,而不需要在这些维度上工作,并且仍然能得到结果呢?
就是这样。我们实际上使用叫做核的东西来实现。相对于 SVM 来说,许多人一开始就接触它了,也可能最后才接触。这可能会让你认为,核主要用于 SVM,但是并不是这样。
核就是相似度函数,它接受两个输出,并使用内积来返回相似度。由于这是个机器学习教程,你们中的一些可能想知道,为什么人们不将核用于机器学习算,以及,我在这里告诉你它们实际上使用了。你不仅仅可以使用核来创建自己的机器学习算法,你可以将现有的机器学习算法翻译为使用核的版本。
核所做的就是允许你,处理许多维度,而不需要花费处理的开销。核的确有个要求:它们依赖于内核。对于这篇教程的目的,“点积”和“内积”可以互相代替。
为了验证我们是否可以使用核,我们需要做的,就是验证我们的特征空间的每个交互,都是内积。我们会从末尾开始,然后返回来确认它。
首先,我们如何在训练之后判断特征的分类呢?

它是不是内积的交互呢?当然是,我们可以将x换成z。
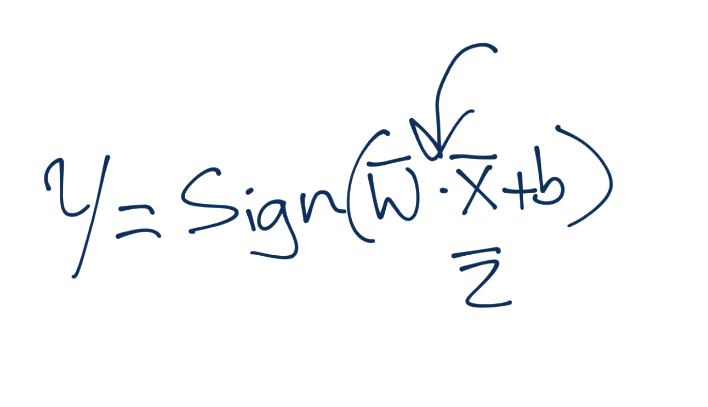
继续,我们打算回顾我们的约束,约束方程为:
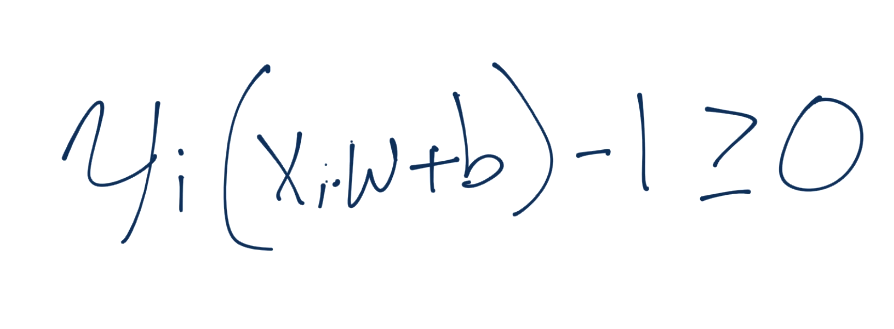
这里如何呢?这个交互式内积嘛?当然,yi(xi.w+b)-1 >= 0等价于yi(xi.w+b) >= 1。所以这里我们可以讲义将x_i替换为z_i。
最后,我们的形式优化方程w如何呢?

它是另一个点积或内积。有任何问题吗?这样:
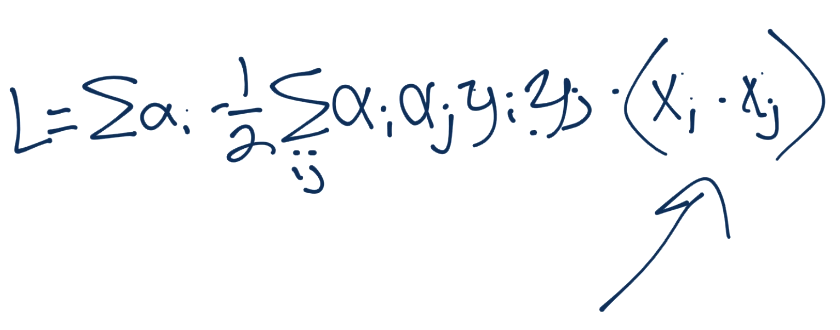
太好了。我们可以使用核。你可能想知道,这个“零开销来计算无穷维度”是什么?好吧,首先我们需要确保我们能这样做。对于零开销的处理,你需要看下一篇教程来了解。
三十、为什么是核
欢迎阅读第三十篇教程。这篇教程中,我们打算继续讨论核,既然我们知道了我们能使用它之后,主要弄清楚如何实际使用它们。
我们之前了解到,我们可以利用核来帮助我们将数据转换为无穷数量的维度,以便找到线性分隔。我们也了解到,核可以让我们处理这些维度,而不需要实际为这些高维度花费开销。通常,核定义为这样:
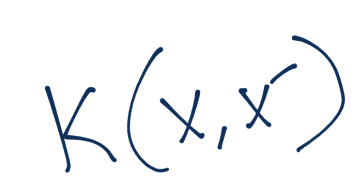
核函数应用于x和x',并等于z和z'的内积,其中z就是z维度的值(我们新的维度空间)。
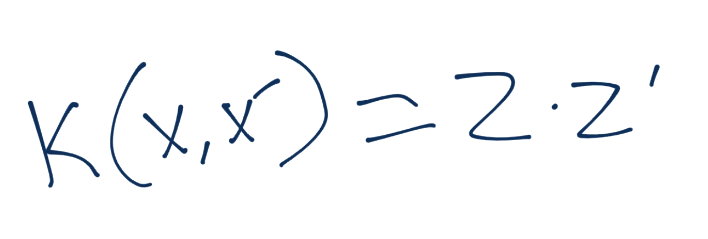
z值就是一些function(x)的结果,这些z值点乘在一起就是我们核函数的结果。
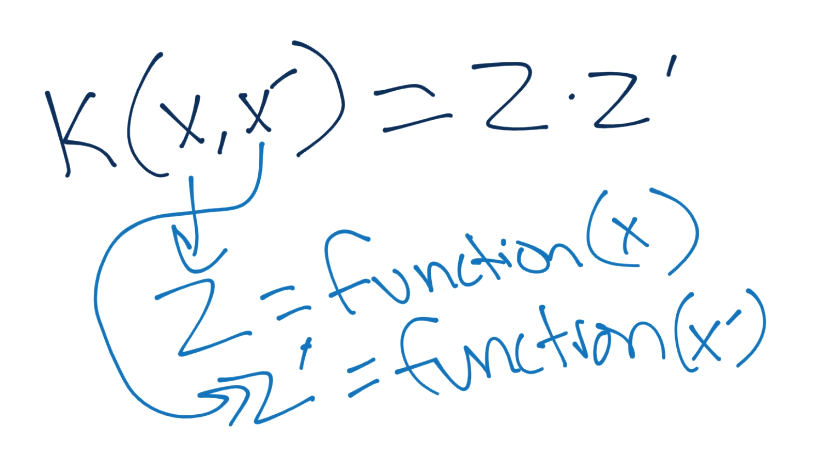
我们仍然需要涉及,它如何节省我们的处理步骤。所以看一个例子吧。我们以多项式来开始,并将多项式核的要求,与简单使用我们的向量来创建二阶多项式来比较:
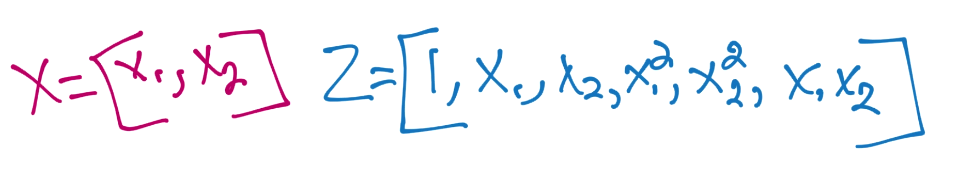
核对x和x'使用相同函数,所以我们对z'也使用相同的东西(x'对二阶多项式)。这里,最终步骤就是计算二者的点积。
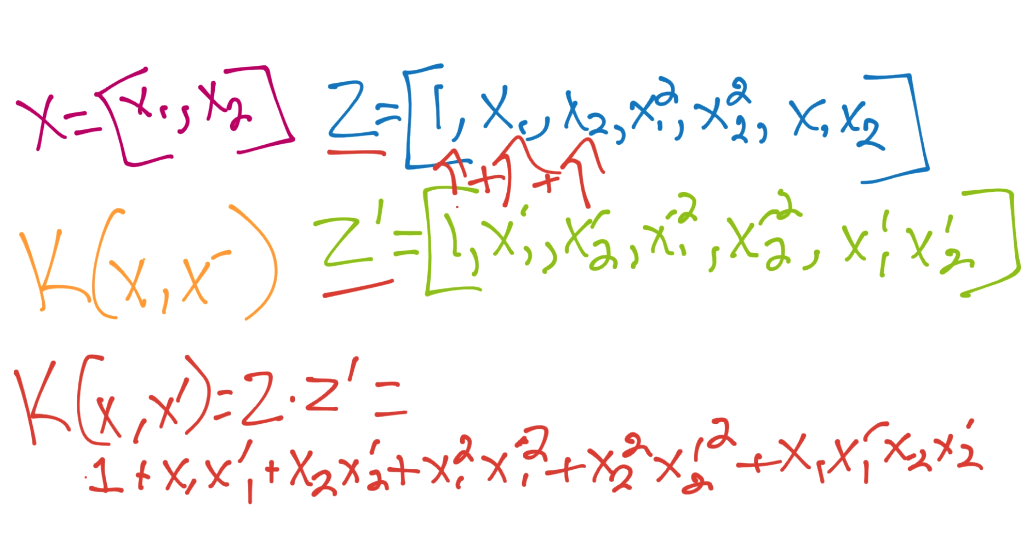
所以所有工作就是手动执行一个和核函数类似的操作。幸运的是,我们的起始维度只有两维。现在让我们考虑多项式核:
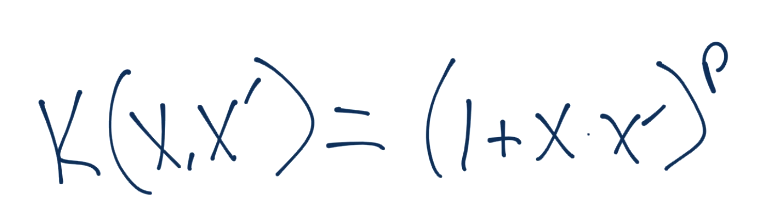
要注意,这里没有提到z。整个核仅仅使用x来计算。你所需的所有东西,就是使用维度数量n和你想使用的权重p来计算。你的方程是这样:
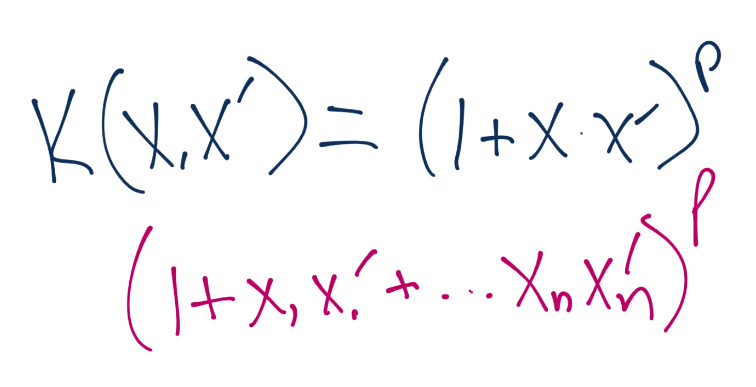
如果你计算了出来,你的新向量是这样,它对应z空间的向量:
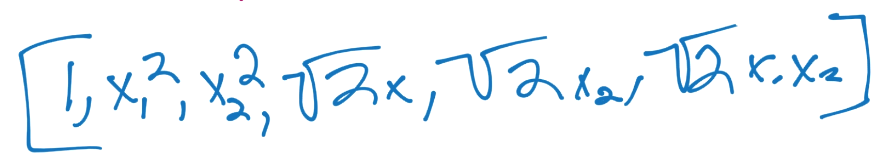
也就是说,你永远不需要继续深入了。你只需要专注于多项式和,它简单返回点积给你,你不需要实际计算向量,之后计算非常大的点积。
也有一些预先创建的核,但是我这里仅仅会展示径向基函数(RBF)核。只是因为它通常是默认使用的核,并且可以将我们带到无限的维度中。
这里的 Gamma 值是后面教程的话题。所以这里以拥有了核,了解了为什么使用它们,如何使用它们,以及它们如何让你处理更大的维度,而不需要花费非常大的处理开销。下一篇教程中,我们打算讨论另一个非线性数据的解决方案,以及数据的过拟合问题。
三十一、软边界 SVM
欢迎阅读第 31 个部分。这篇教程中,我们打算讨论软边界 SVM。
首先,为什么软边界分类器更加优秀,主要有两个原因。一是你的数据可能不是完全线性分隔的,但是很接近了,并且继续使用默认的线性核有更大意义。另一个原因是,即使你使用了某个核,如果你打算使用硬边界的话,你最后也会过拟合。例如,考虑这个:
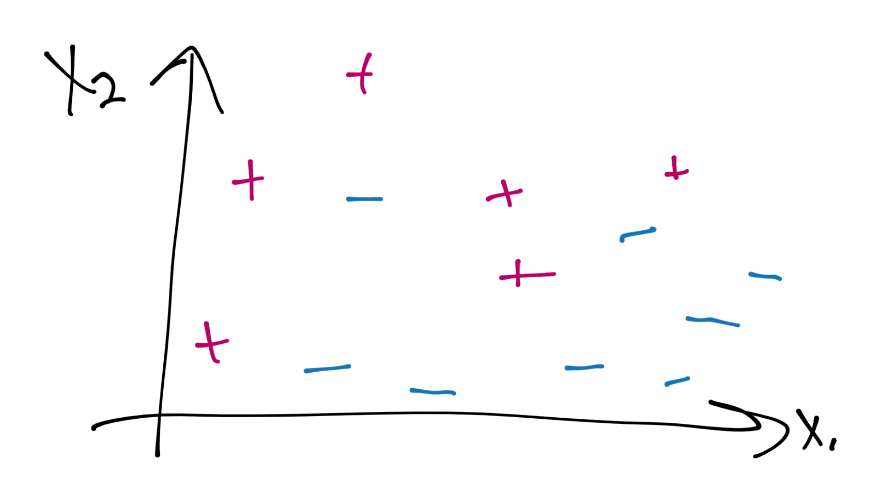
这里是一个数据案例,当前并不是线性可分的。假设使用硬边界(也就是我们之前看到的那种),我们可能使用核来生成这样的决策边界:
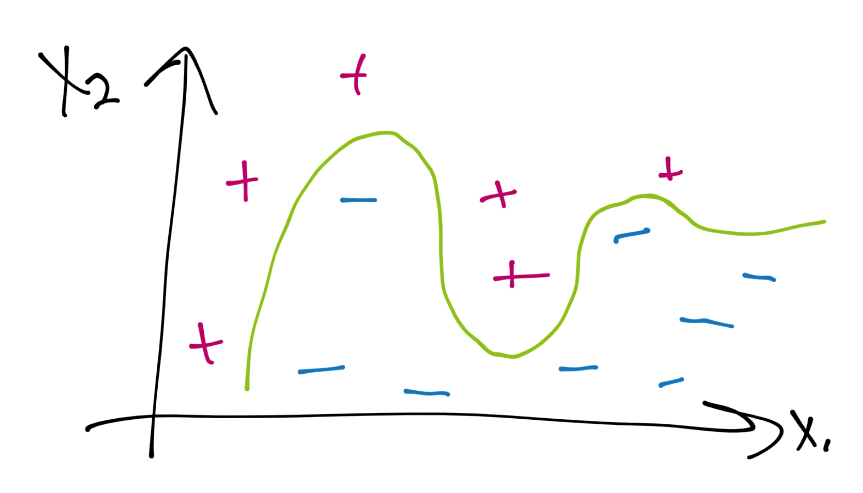
下面,注意我的绘图工具中的缺陷,让我们绘制支持向量平面,并圈出支持向量:
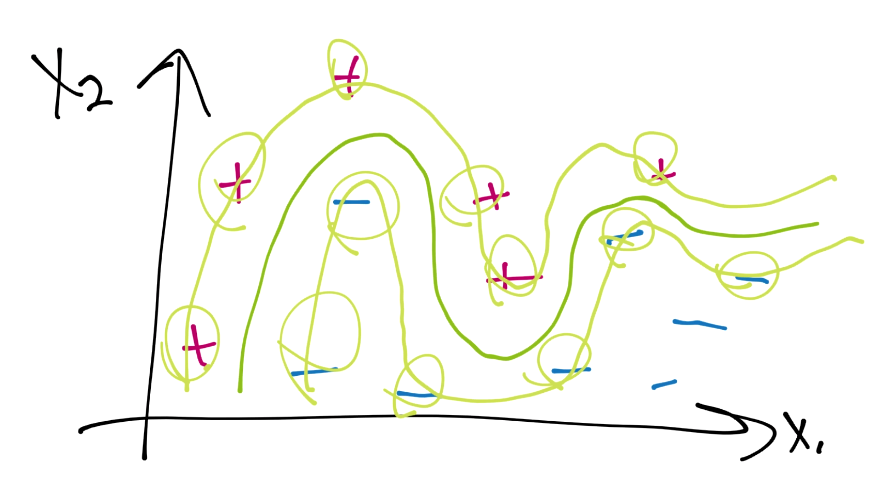
这里,每个正向的数据样例都是支持向量,只有两个负向分类不是支持向量。这个信号就是可能过拟合了,我们应该避免它。因为,当我们用它来预测未来的点时,我们就没有余地了,并且可能会错误分类新的数据。如果我们这样做,会怎么样呢?
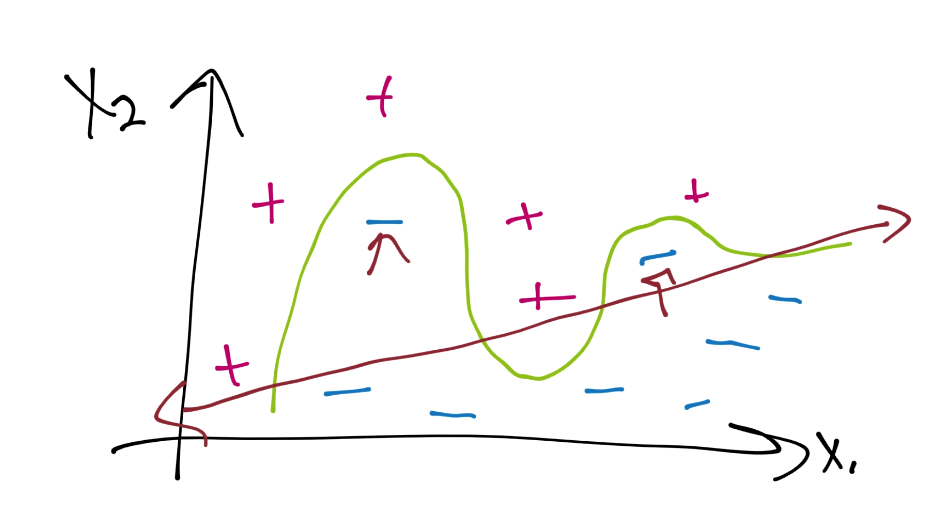
我们有一些错误或者误差,由箭头标记,但是这个可能能够更好地为将来的数据集分类。我们这里就拥有了“软边界”分类器,它允许一些误差上的“弹性”,我们可以在优化过程中获得它。
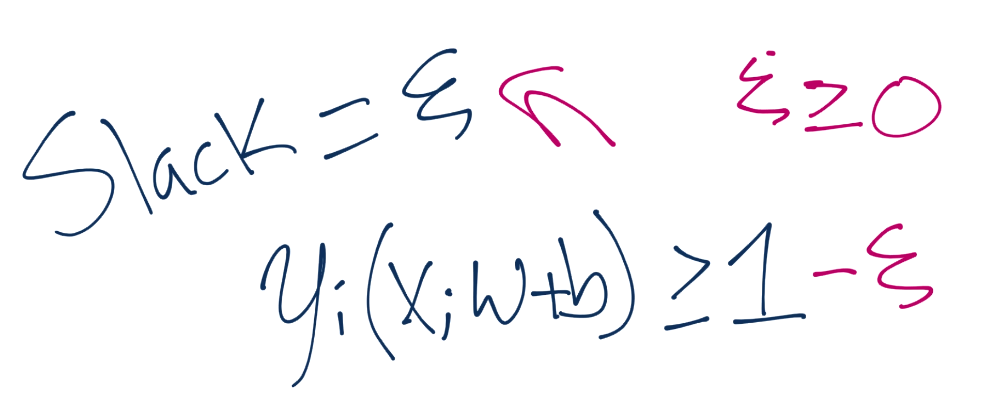
我们的新的优化就是上面的计算,其中弹性大于等于 0。弹性越接近 0,就越接近“硬边界”。弹性越高,边界就越软。如果弹性是 0,我们就得到了一个典型的硬边界分类器。但是你可能能够菜刀,我们希望最小化弹性。为此,我们将其添加到向量w的模的最小值中。
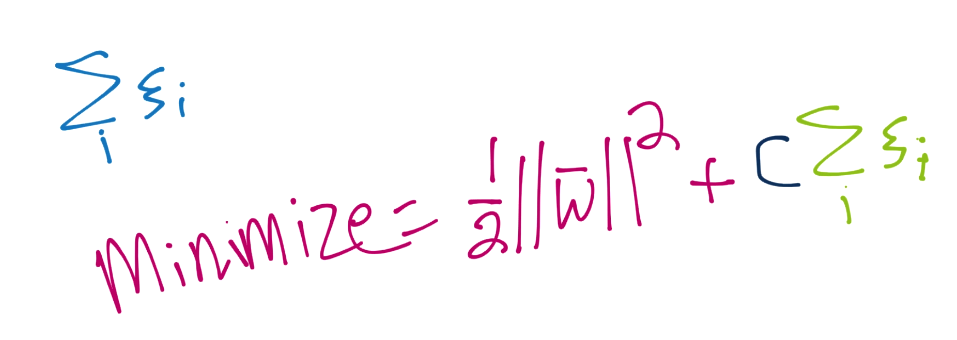
因此,我们实际上打算最小化1/2||w||^2 + C * 所有使用的弹性之和。使用它,我们引入了另一个变量C。C是个系数,关于我们打算让弹性对方程的剩余部分有多少影响。C阅读,弹性的和与向量w的模相比,就越不重要,反之亦然。多数情况下,C的值默认为 1。
所以这里你了解了软边界 SVM,以及为什么打算使用它。下面,我们打算展示一些样例代码,它们由软边界、核和 CVXOPT 组成。
三十二、核、软边界和使用 Python 和 CVXOPT 的平方规划
欢迎阅读第三十二篇机器学习教程。这篇教程中,我们打算展示核、软边界的 Python 版本,并使用 CVXOPT 来解决平方规划问题。
在这个简短的章节中,我打算主要向你分享其它资源,你应该想要使用 Python 和 CVXOPT 深入研究 SVM 或者平方规划。为了开始,你可以阅读 CVXOPT 平方规划文档,来深入了解 Python 中的平方规划。你也可以查看 CVXOPT 平方规划示例。
对于 CVXOPT 的更加深入的平方规划示例,请查看这个 PDF。
最后,我们打算看一看来自 Mathieu Blondel 的博客的一些代码,它由核、软边界 SVM 以及 CVXOPT 平方规划组成。所有代码都优于我写的任何东西。
# Mathieu Blondel, September 2010
# License: BSD 3 clause
# http://www.mblondel.org/journal/2010/09/19/support-vector-machines-in-python/
# visualizing what translating to another dimension does
# and bringing back to 2D:
# https://www.youtube.com/watch?v=3liCbRZPrZA
# Docs: http://cvxopt.org/userguide/coneprog.html#quadratic-programming
# Docs qp example: http://cvxopt.org/examples/tutorial/qp.html
# Nice tutorial:
# https://courses.csail.mit.edu/6.867/wiki/images/a/a7/Qp-cvxopt.pdf
import numpy as np
from numpy import linalg
import cvxopt
import cvxopt.solvers
def linear_kernel(x1, x2):
return np.dot(x1, x2)
def polynomial_kernel(x, y, p=3):
return (1 + np.dot(x, y)) ** p
def gaussian_kernel(x, y, sigma=5.0):
return np.exp(-linalg.norm(x-y)**2 / (2 * (sigma ** 2)))
class SVM(object):
def __init__(self, kernel=linear_kernel, C=None):
self.kernel = kernel
self.C = C
if self.C is not None: self.C = float(self.C)
def fit(self, X, y):
n_samples, n_features = X.shape
# Gram matrix
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
for j in range(n_samples):
K[i,j] = self.kernel(X[i], X[j])
P = cvxopt.matrix(np.outer(y,y) * K)
q = cvxopt.matrix(np.ones(n_samples) * -1)
A = cvxopt.matrix(y, (1,n_samples))
b = cvxopt.matrix(0.0)
if self.C is None:
G = cvxopt.matrix(np.diag(np.ones(n_samples) * -1))
h = cvxopt.matrix(np.zeros(n_samples))
else:
tmp1 = np.diag(np.ones(n_samples) * -1)
tmp2 = np.identity(n_samples)
G = cvxopt.matrix(np.vstack((tmp1, tmp2)))
tmp1 = np.zeros(n_samples)
tmp2 = np.ones(n_samples) * self.C
h = cvxopt.matrix(np.hstack((tmp1, tmp2)))
# solve QP problem
solution = cvxopt.solvers.qp(P, q, G, h, A, b)
# Lagrange multipliers
a = np.ravel(solution['x'])
# Support vectors have non zero lagrange multipliers
sv = a > 1e-5
ind = np.arange(len(a))[sv]
self.a = a[sv]
self.sv = X[sv]
self.sv_y = y[sv]
print("%d support vectors out of %d points" % (len(self.a), n_samples))
# Intercept
self.b = 0
for n in range(len(self.a)):
self.b += self.sv_y[n]
self.b -= np.sum(self.a * self.sv_y * K[ind[n],sv])
self.b /= len(self.a)
# Weight vector
if self.kernel == linear_kernel:
self.w = np.zeros(n_features)
for n in range(len(self.a)):
self.w += self.a[n] * self.sv_y[n] * self.sv[n]
else:
self.w = None
def project(self, X):
if self.w is not None:
return np.dot(X, self.w) + self.b
else:
y_predict = np.zeros(len(X))
for i in range(len(X)):
s = 0
for a, sv_y, sv in zip(self.a, self.sv_y, self.sv):
s += a * sv_y * self.kernel(X[i], sv)
y_predict[i] = s
return y_predict + self.b
def predict(self, X):
return np.sign(self.project(X))
if __name__ == "__main__":
import pylab as pl
def gen_lin_separable_data():
# generate training data in the 2-d case
mean1 = np.array([0, 2])
mean2 = np.array([2, 0])
cov = np.array([[0.8, 0.6], [0.6, 0.8]])
X1 = np.random.multivariate_normal(mean1, cov, 100)
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 100)
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def gen_non_lin_separable_data():
mean1 = [-1, 2]
mean2 = [1, -1]
mean3 = [4, -4]
mean4 = [-4, 4]
cov = [[1.0,0.8], [0.8, 1.0]]
X1 = np.random.multivariate_normal(mean1, cov, 50)
X1 = np.vstack((X1, np.random.multivariate_normal(mean3, cov, 50)))
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 50)
X2 = np.vstack((X2, np.random.multivariate_normal(mean4, cov, 50)))
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def gen_lin_separable_overlap_data():
# generate training data in the 2-d case
mean1 = np.array([0, 2])
mean2 = np.array([2, 0])
cov = np.array([[1.5, 1.0], [1.0, 1.5]])
X1 = np.random.multivariate_normal(mean1, cov, 100)
y1 = np.ones(len(X1))
X2 = np.random.multivariate_normal(mean2, cov, 100)
y2 = np.ones(len(X2)) * -1
return X1, y1, X2, y2
def split_train(X1, y1, X2, y2):
X1_train = X1[:90]
y1_train = y1[:90]
X2_train = X2[:90]
y2_train = y2[:90]
X_train = np.vstack((X1_train, X2_train))
y_train = np.hstack((y1_train, y2_train))
return X_train, y_train
def split_test(X1, y1, X2, y2):
X1_test = X1[90:]
y1_test = y1[90:]
X2_test = X2[90:]
y2_test = y2[90:]
X_test = np.vstack((X1_test, X2_test))
y_test = np.hstack((y1_test, y2_test))
return X_test, y_test
def plot_margin(X1_train, X2_train, clf):
def f(x, w, b, c=0):
# given x, return y such that [x,y] in on the line
# w.x + b = c
return (-w[0] * x - b + c) / w[1]
pl.plot(X1_train[:,0], X1_train[:,1], "ro")
pl.plot(X2_train[:,0], X2_train[:,1], "bo")
pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g")
# w.x + b = 0
a0 = -4; a1 = f(a0, clf.w, clf.b)
b0 = 4; b1 = f(b0, clf.w, clf.b)
pl.plot([a0,b0], [a1,b1], "k")
# w.x + b = 1
a0 = -4; a1 = f(a0, clf.w, clf.b, 1)
b0 = 4; b1 = f(b0, clf.w, clf.b, 1)
pl.plot([a0,b0], [a1,b1], "k--")
# w.x + b = -1
a0 = -4; a1 = f(a0, clf.w, clf.b, -1)
b0 = 4; b1 = f(b0, clf.w, clf.b, -1)
pl.plot([a0,b0], [a1,b1], "k--")
pl.axis("tight")
pl.show()
def plot_contour(X1_train, X2_train, clf):
pl.plot(X1_train[:,0], X1_train[:,1], "ro")
pl.plot(X2_train[:,0], X2_train[:,1], "bo")
pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g")
X1, X2 = np.meshgrid(np.linspace(-6,6,50), np.linspace(-6,6,50))
X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))])
Z = clf.project(X).reshape(X1.shape)
pl.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower')
pl.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower')
pl.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower')
pl.axis("tight")
pl.show()
def test_linear():
X1, y1, X2, y2 = gen_lin_separable_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM()
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_margin(X_train[y_train==1], X_train[y_train==-1], clf)
def test_non_linear():
X1, y1, X2, y2 = gen_non_lin_separable_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM(polynomial_kernel)
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_contour(X_train[y_train==1], X_train[y_train==-1], clf)
def test_soft():
X1, y1, X2, y2 = gen_lin_separable_overlap_data()
X_train, y_train = split_train(X1, y1, X2, y2)
X_test, y_test = split_test(X1, y1, X2, y2)
clf = SVM(C=1000.1)
clf.fit(X_train, y_train)
y_predict = clf.predict(X_test)
correct = np.sum(y_predict == y_test)
print("%d out of %d predictions correct" % (correct, len(y_predict)))
plot_contour(X_train[y_train==1], X_train[y_train==-1], clf)
#test_linear()
#test_non_linear()
test_soft()
如果你想要让我执行这个代码,你可以查看这个视频。我会仅仅提及,你可能不需要使用 CVXOPT。多数人用于 SVM 的库是 LibSVM。
大家都说,这个代码可以让你理解内部的工作原理,并不是为了让你实际创建一个健壮的 SVM,超过你可以自由使用的那个。
下一篇教程中,我们打算再讨论一个 SVM 的概念,它就是当你拥有多于两个分组时,你该怎么做。我们也会在总结中,浏览 Sklearn 的 SVM 的所有参数,因为我们很少涉及这个话题。
第三十三章 支持向量机的参数
原文:Support Vector Machine Parameters
译者:飞龙
欢迎阅读第三十三篇教程,这篇教程中,我们打算通过解释如何处理多于 2 个分类,以及卢兰 Sklearn 的 SVM 的参数,来对 SVM 做个收尾,并且让你见识一下用于 SVM 的现代方法论。
首先,你已经学到了,SVM 是个二元分类器。也就是说,任何时候,SVM 的最优化都只能将一个分组与另一个分组分离。之后问题是我们如何对三个或更多分组分类。通常,方法就是“一对其它”(OVR)。这里的理念就是,将每个分组从其余的分组分离。例如,为了分类三个分组(1,2 和 3),你应该首先将 1 从 2 和 3 分离。之后将 2 从 1 和 3。最后将 3 从 1 和 2 分离。这样有一些问题,因为类似置信度的东西,可能对于每个分类边界都不同,以及分隔边界可能有一些缺陷,因为有一些不仅仅是正向和负向的东西,你将一个分组与其它三个比较。假设最开始有一个均衡的数据集,也就是说每个分类的边界可能是不均衡的。
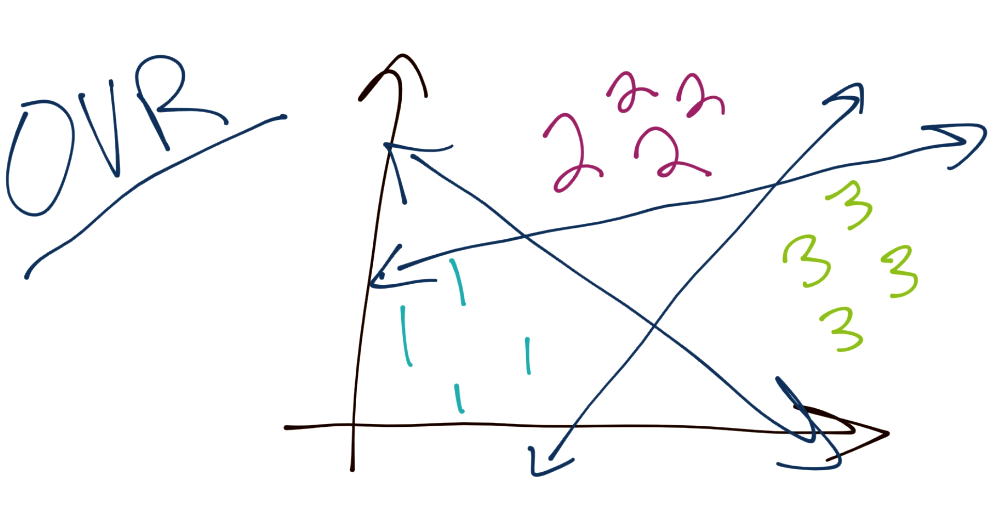
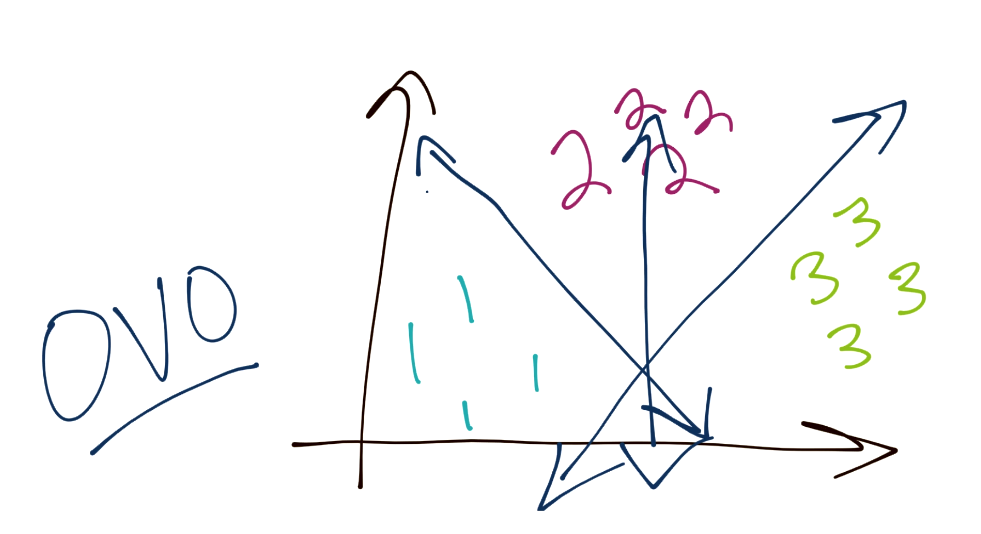
另一个方法是“一对一”(OVO)。这个情况下,考虑你总共拥有三个分组。它的工作方式是,你的边界从 1 分离 3,以及从 1 分离 2,并且对其余分类重复这个过程。这样,边界就会更均衡。
第一个参数是C。它告诉你这是一个软边界分类器。你可以按需调整C,并且可以使C足够高来创建硬边界分类器。C是||w||的软边界优化函数。
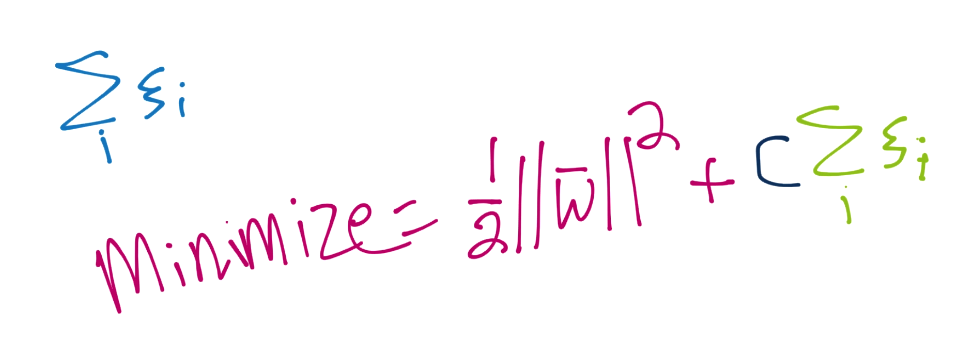
C的默认值是 1,并且多数情况下都很好。
下面我们有个kernel的选项。这里默认是rbf核,但是你可以调整为linear,poly(多项式)和sigmoid核,甚至你选择或设计的自定义核。
然后,还有degree值,默认为 3,这个是多项式的阶数,如果你将poly用于kernel参数的话。
gamma是你为rbf核设置 Gamma 值的地方。你应该将其保留为auto。
coef0允许你调整核函数的独立项,但是你应该保留不变,并且它只用于多项式和 sigmoid 核。
probability参数项可能对你很使用。回忆 KNN 算法不仅仅拥有模型准确度,每个预测还拥有置信度。SVM 本质上没有这个属性,但是你可以使用probability参数来获取一种形式。这是个开销大的功能,但是可能对你来说足够重要,或者默认值为False。
下面是shrinking布尔值,它默认为True。这个用于表示你是否将启发式用于 SVM 的优化,它使用了序列最小优化(SMO)。你应该将其保留为True,因为它可以极大提升你的性能,并且只损失一点点准确性。
tol参数设置了 SVM 的容差。前面说过yi(xi.w+b)-1 >= 0。对于 SVM 来说,所有值都必须大于等于 0,每一边至少一个值要等于 0,这就是你的支持向量。由于你不可能让值(浮点数)完全等于 0,你需要设置一个容差来获取一些弹性空间。Sklearn 中默认的 tol是1e-3,也就是 0.001。
下一个重要的参数是max_iter,它是你可以为平方规划设置最大迭代次数的地方。默认值为-1,也就是没有限制。
decision_function_shape是一对一(OVO),或者一对其它(OVR),那就是教程开始讨论的概念。
random_state用于概率估计中的种子,如果你打算指定的话。
除了这些参数,我们还有几个属性。
support_提供了支持向量的索引。support_vectors_提供了实际的支持向量。n_support_是支持向量的个数,如果你的数据集有一些统计问题,将它与你的数据集尺寸相比非常实用。最后三个参数是dual_coef_、coef_和intercept_,如果你打算绘制 SVM,会非常实用。
SVM 就讲完了。下一个话题是聚类。