朴素贝叶斯分类器

来源：http://blog.csdn.net/u011067360/article/details/22890465

贝叶斯定理

贝叶斯定理解决了现实生活里经常遇到的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率：

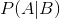表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：。

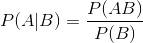贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。

下面不加证明地直接给出贝叶斯定理：

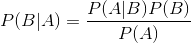
朴素贝叶斯分类的原理与流程

朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素。

朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。

朴素贝叶斯分类器应用的学习任务中，每个实例x可由属性值的合取描述，而目标函数f(x)从某有限集合V中取值。学习器被提供一系列关于目标函数的训练样例，以及新实例（描述为属性值的元组）<a1,a2…an>，然后要求预测新实例的目标值（或分类）。

贝叶斯方法的新实例分类目标是在给定描述实例的属性值<a1,a2…an>下，得到最可能的目标值VMAP。

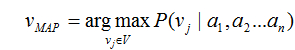
可使用贝叶斯公式将此表达式重写为

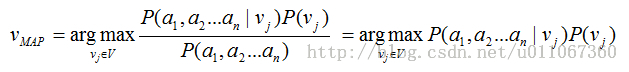（1）

现在要做的是基于训练数据估计（1）式中两个数据项的值。估计每个P(vj)很容易，只要计算每个目标值vj出现在训练数据中的频率就可以。

然而，除非有一非常大的训练数据的集合，否则用这样方法估计不同的P(a1,a2…an|vj)项不太可行。

问题在于这些项的数量等于可能实例的数量乘以可能目标值的数量。因此为获得合理的估计，实例空间中每个实例必须出现多次。

朴素贝叶斯分类器基于一个简单的假定：在给定目标值时属性值之间相互条件独立。

换言之，该假定说明给定实例的目标值情况下，观察到联合的a1,a2…an的概率正好是对每个单独属性的概率乘积：

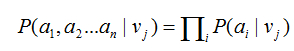
将其代入（1）式中，可得到朴素贝叶斯分类器所使用的方法：

朴素贝叶斯分类器：

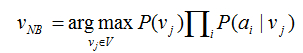
其中vNB表示朴素贝叶斯分类器输出的目标值。

注意在朴素贝叶斯分类器中，须从训练数据中估计的不同P(ai|vj)项的数量只是不同的属性值数量乘以不同目标值数量——这比要估计P(a1,a2…an|vj)项所需的量小得多。

概括地讲，朴素贝叶斯学习方法需要估计不同的P(vj)和P(ai|vj)项，基于它们在训练数据上的频率。这些估计对应了待学习的假设。然后该假设使用上面式中的规则来分类新实例。只要所需的条件独立性能够被满足，朴素贝叶斯分类vNB等于MAP分类。

朴素贝叶斯学习方法和其他已介绍的学习方法之间有一有趣的差别：没有明确的搜索假设空间的过程（这里，可能假设的空间为可被赋予不同的P(vj)和P(ai|vj)项的可能值。相反，假设的形成不需要搜索，只是简单地计算训练样例中不同数据组合的出现频率）。

朴素贝叶斯分类的正式定义如下：

1、设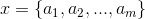为一个待分类项，而每个a为x的一个特征属性。

2、有类别集合。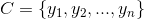

3、计算。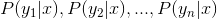

4、如果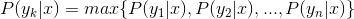，则。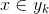

那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。

2、统计得到在各类别下各个特征属性的条件概率估计。即。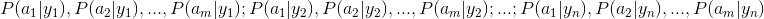

3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

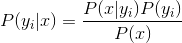
因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

朴素贝叶斯分类实例：按照某人是否要打网球来划分天气

Day Outlook Temperature Humidity Wind PlayTennis
D1 Sunny Hot High Weak No
D2 Sunny Hot High Strong No
D3 Overcast Hot High Weak Yes
D4 Rain Mild High Weak Yes
D5 Rain Cool Normal Weak Yes
D6 Rain Cool Normal Strong No
D7 Overcast Cool Normal Strong Yes
D8 Sunny Mild High Weak No
D9 Sunny Cool Normal Weak Yes
D10 Rain Mild Normal Weak Yes
D11 Sunny Mild Normal Strong Yes
D12 Overcast Mild High Strong Yes
D13 Overcast Hot Normal Weak Yes
D14 Rain Mild High Strong No

这里我们使用此表中的数据结合朴素贝叶斯分类器来分类下面的新实例：

Outlook=sunny, Temperature=cool,Humidity=high,Wind=strong

我们的任务是对此新实例预测目标概念PlayTennis 的目标值（yes 或no）。将上面式子应用到当前的任务，目标值vNB 由下式给出：

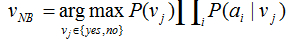
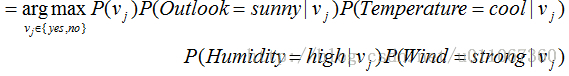（2）

注意在最后一个表达式中ai已经用新实例的特定属性值实例化了。为计算vNB，现在需要10个概率，它们都可以训练数据中估计出。

首先不同目标值的概率可以基于这14个训练样例的频率很容易地估计出：

P(PlayTennis=yes)=9/14=0.64
P(PlayTennis=no)=5/14=0.36

相似地，可以估计出条件概率，例如对于Wind=Strong有：

P(Wind=strong|PlayTennis=yes)=3/9=0.33
P(Wind=strong|PlayTennis=no)=3/5=0.60

使用这些概率估计以及相似的对剩余属性的估计，可按照式（2）计算vNB如下（为简明起见忽略了属性名）。

P(yes)P(sunny|yes)P(cool|yes)P(high|yes)P(strong|yes)=0.0053
P(no)P(sunny|no)P(cool|no)P(high|no)P(strong|no)=0.0206

这样，基于从训练数据中学习到的概率估计，朴素贝叶斯分类器将此实例赋以目标值PlayTennis=no 。

更进一步，通过将上述的量归一化，可计算给定观察值下目标值为no 的条件概率。对于此例，概率为0.0206/(0.0206+0.0053)=0.795。

从数学角度来说，分类问题可做如下定义：

已知集合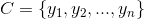：和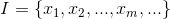，确定映射规则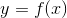，使得任意有且仅有一个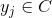使得成立。（不考虑模糊数学里的模糊集情况）

其中C叫做类别集合，其中每一个元素是一个类别，而I叫做项集合，其中每一个元素是一个待分类项，f叫做分类器。分类算法的任务就是构造分类器f。

这里要着重强调，分类问题往往采用经验性方法构造映射规则，即一般情况下的分类问题缺少足够的信息来构造100%正确的映射规则，而是通过对经验数据的学习从而实现一定概率意义上正确的分类，因此所训练出的分类器并不是一定能将每个待分类项准确映射到其分类，分类器的质量与分类器构造方法、待分类数据的特性以及训练样本数量等诸多因素有关。