TensorFlow 教程 #04
保存 & 恢复
by Magnus Erik Hvass Pedersen
/ GitHub / Videos on YouTube
中文翻译 thrillerist/Github
简介
这篇教程展示了如何保存以及恢复神经网络中的变量。在优化的过程中,当验证集上分类准确率提高时,保存神经网络的变量。如果经过1000次迭代还不能提升性能时,就终止优化。然后我们重新载入在验证集上表现最好的变量。
这种策略称为Early-Stopping。它用来避免神经网络的过拟合。(过拟合)会在神经网络训练时间太长时出现,此时神经网络开始学习训练集中的噪声,将导致它误分类新的图像。
这篇教程主要是用神经网络来识别MNIST数据集中的手写数字,过拟合在这里并不是什么大问题。但本教程展示了Early Stopping的思想。
本文基于上一篇教程,你需要了解基本的TensorFlow和附加包Pretty Tensor。其中大量代码和文字与之前教程相似,如果你已经看过就可以快速地浏览本文。
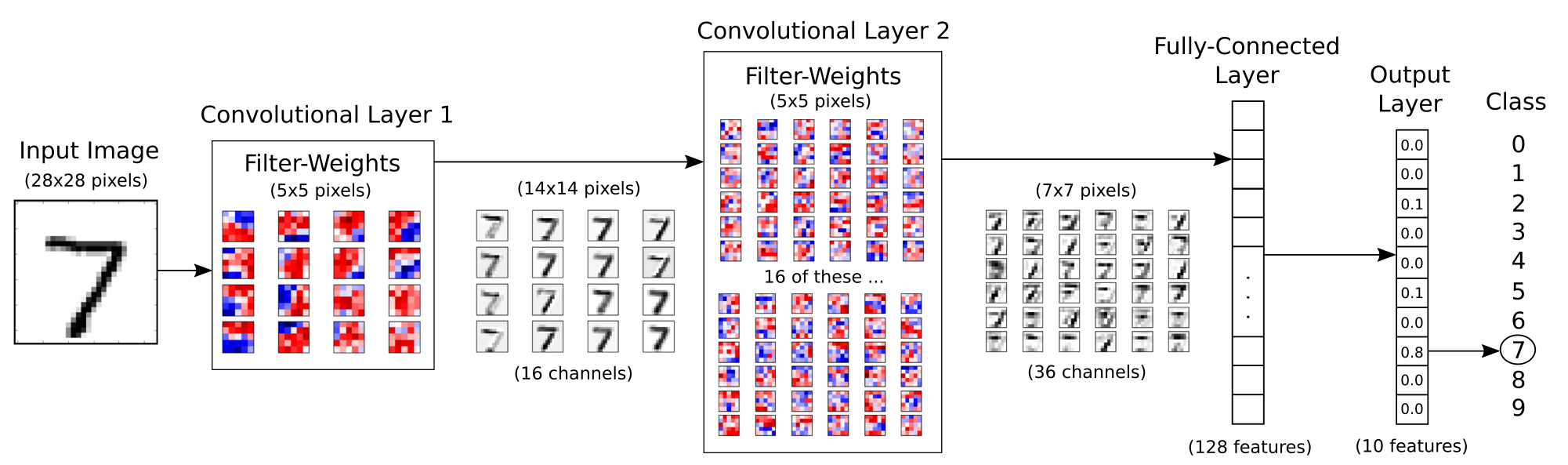
流程图
下面的图表直接显示了之后实现的卷积神经网络中数据的传递。网络有两个卷积层和两个全连接层,最后一层是用来给输入图像分类的。关于网络和卷积的更多细节描述见教程 #02 。
from IPython.display import Image
Image('images/02_network_flowchart.png')
导入
%matplotlib inline
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
from sklearn.metrics import confusion_matrix
import time
from datetime import timedelta
import math
import os
# Use PrettyTensor to simplify Neural Network construction.
import prettytensor as pt
使用Python3.5.2(Anaconda)开发,TensorFlow版本是:
tf.__version__
'0.12.0-rc0'
PrettyTensor 版本:
pt.__version__
'0.7.1'
载入数据
MNIST数据集大约12MB,如果没在给定路径中找到就会自动下载。
from tensorflow.examples.tutorials.mnist import input_data
data = input_data.read_data_sets('data/MNIST/', one_hot=True)
Extracting data/MNIST/train-images-idx3-ubyte.gz
Extracting data/MNIST/train-labels-idx1-ubyte.gz
Extracting data/MNIST/t10k-images-idx3-ubyte.gz
Extracting data/MNIST/t10k-labels-idx1-ubyte.gz
现在已经载入了MNIST数据集,它由70,000张图像和对应的标签(比如图像的类别)组成。数据集分成三份互相独立的子集。我们在教程中只用训练集和测试集。
print("Size of:")
print("- Training-set:\t\t{}".format(len(data.train.labels)))
print("- Test-set:\t\t{}".format(len(data.test.labels)))
print("- Validation-set:\t{}".format(len(data.validation.labels)))
Size of:
- Training-set: 55000
- Test-set: 10000
- Validation-set: 5000
类型标签使用One-Hot编码,这意外每个标签是长为10的向量,除了一个元素之外,其他的都为零。这个元素的索引就是类别的数字,即相应图片中画的数字。我们也需要测试数据集类别数字的整型值,用下面的方法来计算。
data.test.cls = np.argmax(data.test.labels, axis=1)
data.validation.cls = np.argmax(data.validation.labels, axis=1)
数据维度
在下面的源码中,有很多地方用到了数据维度。它们只在一个地方定义,因此我们可以在代码中使用这些数字而不是直接写数字。
# We know that MNIST images are 28 pixels in each dimension.
img_size = 28
# Images are stored in one-dimensional arrays of this length.
img_size_flat = img_size * img_size
# Tuple with height and width of images used to reshape arrays.
img_shape = (img_size, img_size)
# Number of colour channels for the images: 1 channel for gray-scale.
num_channels = 1
# Number of classes, one class for each of 10 digits.
num_classes = 10
用来绘制图片的帮助函数
这个函数用来在3x3的栅格中画9张图像,然后在每张图像下面写出真实类别和预测类别。
def plot_images(images, cls_true, cls_pred=None):
assert len(images) == len(cls_true) == 9
# Create figure with 3x3 sub-plots.
fig, axes = plt.subplots(3, 3)
fig.subplots_adjust(hspace=0.3, wspace=0.3)
for i, ax in enumerate(axes.flat):
# Plot image.
ax.imshow(images[i].reshape(img_shape), cmap='binary')
# Show true and predicted classes.
if cls_pred is None:
xlabel = "True: {0}".format(cls_true[i])
else:
xlabel = "True: {0}, Pred: {1}".format(cls_true[i], cls_pred[i])
# Show the classes as the label on the x-axis.
ax.set_xlabel(xlabel)
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show()
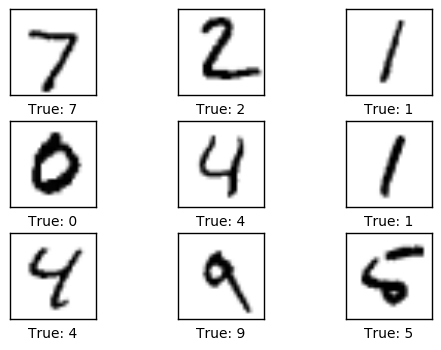
绘制几张图像来看看数据是否正确
# Get the first images from the test-set.
images = data.test.images[0:9]
# Get the true classes for those images.
cls_true = data.test.cls[0:9]
# Plot the images and labels using our helper-function above.
plot_images(images=images, cls_true=cls_true)
TensorFlow图
TensorFlow的全部目的就是使用一个称之为计算图(computational graph)的东西,它会比直接在Python中进行相同计算量要高效得多。TensorFlow比Numpy更高效,因为TensorFlow了解整个需要运行的计算图,然而Numpy只知道某个时间点上唯一的数学运算。
TensorFlow也能够自动地计算需要优化的变量的梯度,使得模型有更好的表现。这是由于图是简单数学表达式的结合,因此整个图的梯度可以用链式法则推导出来。
TensorFlow还能利用多核CPU和GPU,Google也为TensorFlow制造了称为TPUs(Tensor Processing Units)的特殊芯片,它比GPU更快。
一个TensorFlow图由下面几个部分组成,后面会详细描述:
- 占位符变量(Placeholder)用来改变图的输入。
- 模型变量(Model)将会被优化,使得模型表现得更好。
- 模型本质上就是一些数学函数,它根据Placeholder和模型的输入变量来计算一些输出。
- 一个cost度量用来指导变量的优化。
- 一个优化策略会更新模型的变量。
另外,TensorFlow图也包含了一些调试状态,比如用TensorBoard打印log数据,本教程不涉及这些。
占位符 (Placeholder)变量
Placeholder是作为图的输入,我们每次运行图的时候都可能改变它们。将这个过程称为feeding placeholder变量,后面将会描述这个。
首先我们为输入图像定义placeholder变量。这让我们可以改变输入到TensorFlow图中的图像。这也是一个张量(tensor),代表一个多维向量或矩阵。数据类型设置为float32,形状设为[None, img_size_flat],None代表tensor可能保存着任意数量的图像,每张图象是一个长度为img_size_flat的向量。
x = tf.placeholder(tf.float32, shape=[None, img_size_flat], name='x')
卷积层希望x被编码为4维张量,因此我们需要将它的形状转换至[num_images, img_height, img_width, num_channels]。注意img_height == img_width == img_size,如果第一维的大小设为-1, num_images的大小也会被自动推导出来。转换运算如下:
x_image = tf.reshape(x, [-1, img_size, img_size, num_channels])
接下来我们为输入变量x中的图像所对应的真实标签定义placeholder变量。变量的形状是[None, num_classes],这代表着它保存了任意数量的标签,每个标签是长度为num_classes的向量,本例中长度为10。
y_true = tf.placeholder(tf.float32, shape=[None, 10], name='y_true')
我们也可以为class-number提供一个placeholder,但这里用argmax来计算它。这里只是TensorFlow中的一些操作,没有执行什么运算。
y_true_cls = tf.argmax(y_true, dimension=1)
神经网络
这一节用PrettyTensor实现卷积神经网络,这要比直接在TensorFlow中实现来得简单,详见教程 #03。
基本思想就是用一个Pretty Tensor object封装输入张量x_image,它有一个添加新卷积层的帮助函数,以此来创建整个神经网络。Pretty Tensor负责变量分配等等。
x_pretty = pt.wrap(x_image)
现在我们已经将输入图像装到一个PrettyTensor的object中,再用几行代码就可以添加卷积层和全连接层。
注意,在with代码块中,pt.defaults_scope(activation_fn=tf.nn.relu) 把 activation_fn=tf.nn.relu当作每个的层参数,因此这些层都用到了 Rectified Linear Units (ReLU) 。defaults_scope使我们能更方便地修改所有层的参数。
with pt.defaults_scope(activation_fn=tf.nn.relu):
y_pred, loss = x_pretty.\
conv2d(kernel=5, depth=16, name='layer_conv1').\
max_pool(kernel=2, stride=2).\
conv2d(kernel=5, depth=36, name='layer_conv2').\
max_pool(kernel=2, stride=2).\
flatten().\
fully_connected(size=128, name='layer_fc1').\
softmax_classifier(num_classes=num_classes, labels=y_true)
获取权重
下面,我们要绘制神经网络的权重。当使用Pretty Tensor来创建网络时,层的所有变量都是由Pretty Tensoe间接创建的。因此我们要从TensorFlow中获取变量。
我们用layer_conv1 和 layer_conv2代表两个卷积层。这也叫变量作用域(不要与上面描述的defaults_scope混淆了)。PrettyTensor会自动给它为每个层创建的变量命名,因此我们可以通过层的作用域名称和变量名来取得某一层的权重。
函数实现有点笨拙,因为我们不得不用TensorFlow函数get_variable(),它是设计给其他用途的,创建新的变量或重用现有变量。创建下面的帮助函数很简单。
def get_weights_variable(layer_name):
# Retrieve an existing variable named 'weights' in the scope
# with the given layer_name.
# This is awkward because the TensorFlow function was
# really intended for another purpose.
with tf.variable_scope(layer_name, reuse=True):
variable = tf.get_variable('weights')
return variable
借助这个帮助函数我们可以获取变量。这些是TensorFlow的objects。你需要类似的操作来获取变量的内容: contents = session.run(weights_conv1) ,下面会提到这个。
weights_conv1 = get_weights_variable(layer_name='layer_conv1')
weights_conv2 = get_weights_variable(layer_name='layer_conv2')
优化方法
PrettyTensor给我们提供了预测类型标签(y_pred)以及一个需要最小化的损失度量,用来提升神经网络分类图片的能力。
PrettyTensor的文档并没有说明它的损失度量是用cross-entropy还是其他的。但现在我们用AdamOptimizer来最小化损失。
优化过程并不是在这里执行。实际上,还没计算任何东西,我们只是往TensorFlow图中添加了优化器,以便后续操作。
optimizer = tf.train.AdamOptimizer(learning_rate=1e-4).minimize(loss)
性能度量
我们需要另外一些性能度量,来向用户展示这个过程。
首先我们从神经网络输出的y_pred中计算出预测的类别,它是一个包含10个元素的向量。类别数字是最大元素的索引。
y_pred_cls = tf.argmax(y_pred, dimension=1)
然后创建一个布尔向量,用来告诉我们每张图片的真实类别是否与预测类别相同。
correct_prediction = tf.equal(y_pred_cls, y_true_cls)
上面的计算先将布尔值向量类型转换成浮点型向量,这样子False就变成0,True变成1,然后计算这些值的平均数,以此来计算分类的准确度。
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
Saver
为了保存神经网络的变量,我们创建一个称为Saver-object的对象,它用来保存及恢复TensorFlow图的所有变量。在这里并未保存什么东西,(保存操作)在后面的optimize()函数中完成。
saver = tf.train.Saver()
由于(保存操作)常间隔着写在(代码)中,因此保存的文件通常称为checkpoints。
这是用来保存或恢复数据的文件夹。
save_dir = 'checkpoints/'
如果文件夹不存在则创建。
if not os.path.exists(save_dir):
os.makedirs(save_dir)
这是保存checkpoint文件的路径。
save_path = os.path.join(save_dir, 'best_validation')
运行TensorFlow
创建TensorFlow会话(session)
一旦创建了TensorFlow图,我们需要创建一个TensorFlow会话,用来运行图。
session = tf.Session()
初始化变量
变量weights和biases在优化之前需要先进行初始化。我们写一个简单的封装函数,后面会再次调用。
def init_variables():
session.run(tf.global_variables_initializer())
运行函数来初始化变量。
init_variables()
用来优化迭代的帮助函数
在训练集中有50,000张图。用这些图像计算模型的梯度会花很多时间。因此我们利用随机梯度下降的方法,它在优化器的每次迭代里只用到了一小部分的图像。
如果内存耗尽导致电脑死机或变得很慢,你应该试着减少这些数量,但同时可能还需要更优化的迭代。
train_batch_size = 64
每迭代100次下面的优化函数,会计算一次验证集上的分类准确率。如果过了1000次迭代验证准确率还是没有提升,就停止优化。我们需要一些变量来跟踪这个过程。
# Best validation accuracy seen so far.
best_validation_accuracy = 0.0
# Iteration-number for last improvement to validation accuracy.
last_improvement = 0
# Stop optimization if no improvement found in this many iterations.
require_improvement = 1000
函数用来执行一定数量的优化迭代,以此来逐渐改善网络层的变量。在每次迭代中,会从训练集中选择新的一批数据,然后TensorFlow在这些训练样本上执行优化。每100次迭代会打印出(信息),同时计算验证准确率,如果效果有提升的话会将它保存至文件。
# Counter for total number of iterations performed so far.
total_iterations = 0
def optimize(num_iterations):
# Ensure we update the global variables rather than local copies.
global total_iterations
global best_validation_accuracy
global last_improvement
# Start-time used for printing time-usage below.
start_time = time.time()
for i in range(num_iterations):
# Increase the total number of iterations performed.
# It is easier to update it in each iteration because
# we need this number several times in the following.
total_iterations += 1
# Get a batch of training examples.
# x_batch now holds a batch of images and
# y_true_batch are the true labels for those images.
x_batch, y_true_batch = data.train.next_batch(train_batch_size)
# Put the batch into a dict with the proper names
# for placeholder variables in the TensorFlow graph.
feed_dict_train = {x: x_batch,
y_true: y_true_batch}
# Run the optimizer using this batch of training data.
# TensorFlow assigns the variables in feed_dict_train
# to the placeholder variables and then runs the optimizer.
session.run(optimizer, feed_dict=feed_dict_train)
# Print status every 100 iterations and after last iteration.
if (total_iterations % 100 == 0) or (i == (num_iterations - 1)):
# Calculate the accuracy on the training-batch.
acc_train = session.run(accuracy, feed_dict=feed_dict_train)
# Calculate the accuracy on the validation-set.
# The function returns 2 values but we only need the first.
acc_validation, _ = validation_accuracy()
# If validation accuracy is an improvement over best-known.
if acc_validation > best_validation_accuracy:
# Update the best-known validation accuracy.
best_validation_accuracy = acc_validation
# Set the iteration for the last improvement to current.
last_improvement = total_iterations
# Save all variables of the TensorFlow graph to file.
saver.save(sess=session, save_path=save_path)
# A string to be printed below, shows improvement found.
improved_str = '*'
else:
# An empty string to be printed below.
# Shows that no improvement was found.
improved_str = ''
# Status-message for printing.
msg = "Iter: {0:>6}, Train-Batch Accuracy: {1:>6.1%}, Validation Acc: {2:>6.1%} {3}"
# Print it.
print(msg.format(i + 1, acc_train, acc_validation, improved_str))
# If no improvement found in the required number of iterations.
if total_iterations - last_improvement > require_improvement:
print("No improvement found in a while, stopping optimization.")
# Break out from the for-loop.
break
# Ending time.
end_time = time.time()
# Difference between start and end-times.
time_dif = end_time - start_time
# Print the time-usage.
print("Time usage: " + str(timedelta(seconds=int(round(time_dif)))))
用来绘制错误样本的帮助函数
函数用来绘制测试集中被误分类的样本。
def plot_example_errors(cls_pred, correct):
# This function is called from print_test_accuracy() below.
# cls_pred is an array of the predicted class-number for
# all images in the test-set.
# correct is a boolean array whether the predicted class
# is equal to the true class for each image in the test-set.
# Negate the boolean array.
incorrect = (correct == False)
# Get the images from the test-set that have been
# incorrectly classified.
images = data.test.images[incorrect]
# Get the predicted classes for those images.
cls_pred = cls_pred[incorrect]
# Get the true classes for those images.
cls_true = data.test.cls[incorrect]
# Plot the first 9 images.
plot_images(images=images[0:9],
cls_true=cls_true[0:9],
cls_pred=cls_pred[0:9])
绘制混淆(confusion)矩阵的帮助函数
def plot_confusion_matrix(cls_pred):
# This is called from print_test_accuracy() below.
# cls_pred is an array of the predicted class-number for
# all images in the test-set.
# Get the true classifications for the test-set.
cls_true = data.test.cls
# Get the confusion matrix using sklearn.
cm = confusion_matrix(y_true=cls_true,
y_pred=cls_pred)
# Print the confusion matrix as text.
print(cm)
# Plot the confusion matrix as an image.
plt.matshow(cm)
# Make various adjustments to the plot.
plt.colorbar()
tick_marks = np.arange(num_classes)
plt.xticks(tick_marks, range(num_classes))
plt.yticks(tick_marks, range(num_classes))
plt.xlabel('Predicted')
plt.ylabel('True')
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show()
计算分类的帮助函数
这个函数用来计算图像的预测类别,同时返回一个代表每张图像分类是否正确的布尔数组。
由于计算可能会耗费太多内存,就分批处理。如果你的电脑死机了,试着降低batch-size。
# Split the data-set in batches of this size to limit RAM usage.
batch_size = 256
def predict_cls(images, labels, cls_true):
# Number of images.
num_images = len(images)
# Allocate an array for the predicted classes which
# will be calculated in batches and filled into this array.
cls_pred = np.zeros(shape=num_images, dtype=np.int)
# Now calculate the predicted classes for the batches.
# We will just iterate through all the batches.
# There might be a more clever and Pythonic way of doing this.
# The starting index for the next batch is denoted i.
i = 0
while i < num_images:
# The ending index for the next batch is denoted j.
j = min(i + batch_size, num_images)
# Create a feed-dict with the images and labels
# between index i and j.
feed_dict = {x: images[i:j, :],
y_true: labels[i:j, :]}
# Calculate the predicted class using TensorFlow.
cls_pred[i:j] = session.run(y_pred_cls, feed_dict=feed_dict)
# Set the start-index for the next batch to the
# end-index of the current batch.
i = j
# Create a boolean array whether each image is correctly classified.
correct = (cls_true == cls_pred)
return correct, cls_pred
计算测试集上的预测类别。
def predict_cls_test():
return predict_cls(images = data.test.images,
labels = data.test.labels,
cls_true = data.test.cls)
计算验证集上的预测类别。
def predict_cls_validation():
return predict_cls(images = data.validation.images,
labels = data.validation.labels,
cls_true = data.validation.cls)
分类准确率的帮助函数
这个函数计算了给定布尔数组的分类准确率,布尔数组表示每张图像是否被正确分类。比如, cls_accuracy([True, True, False, False, False]) = 2/5 = 0.4。
def cls_accuracy(correct):
# Calculate the number of correctly classified images.
# When summing a boolean array, False means 0 and True means 1.
correct_sum = correct.sum()
# Classification accuracy is the number of correctly classified
# images divided by the total number of images in the test-set.
acc = float(correct_sum) / len(correct)
return acc, correct_sum
计算验证集上的分类准确率。
def validation_accuracy():
# Get the array of booleans whether the classifications are correct
# for the validation-set.
# The function returns two values but we only need the first.
correct, _ = predict_cls_validation()
# Calculate the classification accuracy and return it.
return cls_accuracy(correct)
展示性能的帮助函数
函数用来打印测试集上的分类准确率。
为测试集上的所有图片计算分类会花费一段时间,因此我们直接从这个函数里调用上面的函数,这样就不用每个函数都重新计算分类。
def print_test_accuracy(show_example_errors=False,
show_confusion_matrix=False):
# For all the images in the test-set,
# calculate the predicted classes and whether they are correct.
correct, cls_pred = predict_cls_test()
# Classification accuracy and the number of correct classifications.
acc, num_correct = cls_accuracy(correct)
# Number of images being classified.
num_images = len(correct)
# Print the accuracy.
msg = "Accuracy on Test-Set: {0:.1%} ({1} / {2})"
print(msg.format(acc, num_correct, num_images))
# Plot some examples of mis-classifications, if desired.
if show_example_errors:
print("Example errors:")
plot_example_errors(cls_pred=cls_pred, correct=correct)
# Plot the confusion matrix, if desired.
if show_confusion_matrix:
print("Confusion Matrix:")
plot_confusion_matrix(cls_pred=cls_pred)
绘制卷积权重的帮助函数
def plot_conv_weights(weights, input_channel=0):
# Assume weights are TensorFlow ops for 4-dim variables
# e.g. weights_conv1 or weights_conv2.
# Retrieve the values of the weight-variables from TensorFlow.
# A feed-dict is not necessary because nothing is calculated.
w = session.run(weights)
# Print mean and standard deviation.
print("Mean: {0:.5f}, Stdev: {1:.5f}".format(w.mean(), w.std()))
# Get the lowest and highest values for the weights.
# This is used to correct the colour intensity across
# the images so they can be compared with each other.
w_min = np.min(w)
w_max = np.max(w)
# Number of filters used in the conv. layer.
num_filters = w.shape[3]
# Number of grids to plot.
# Rounded-up, square-root of the number of filters.
num_grids = math.ceil(math.sqrt(num_filters))
# Create figure with a grid of sub-plots.
fig, axes = plt.subplots(num_grids, num_grids)
# Plot all the filter-weights.
for i, ax in enumerate(axes.flat):
# Only plot the valid filter-weights.
if i<num_filters:
# Get the weights for the i'th filter of the input channel.
# The format of this 4-dim tensor is determined by the
# TensorFlow API. See Tutorial #02 for more details.
img = w[:, :, input_channel, i]
# Plot image.
ax.imshow(img, vmin=w_min, vmax=w_max,
interpolation='nearest', cmap='seismic')
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show()
优化之前的性能
测试集上的准确度很低,这是由于模型只做了初始化,并没做任何优化,所以它只是对图像做随机分类。
print_test_accuracy()
Accuracy on Test-Set: 8.5% (849 / 10000)
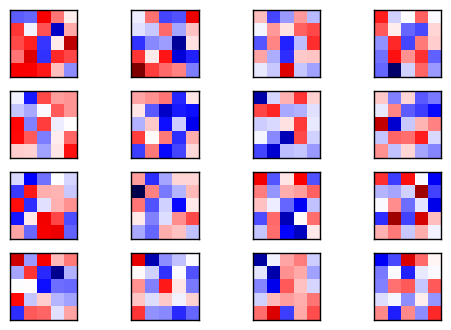
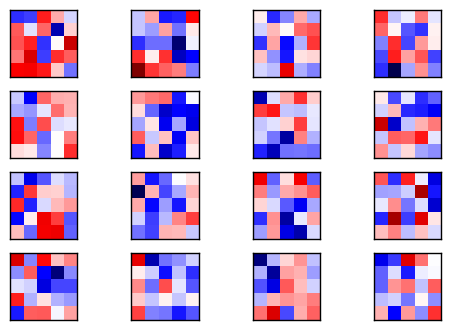
卷积权重是随机的,但也很难把它与下面优化过的权重区分开来。这里也展示了平均值和标准差,因此我们可以看看是否有差别。
plot_conv_weights(weights=weights_conv1)
Mean: 0.00880, Stdev: 0.28635
10,000次优化迭代后的性能
现在我们进行了10,000次优化迭代,并且,当经过1000次迭代验证集上的性能却没有提升时就停止优化。
星号 * 代表验证集上的分类准确度有提升。
optimize(num_iterations=10000)
Iter: 100, Train-Batch Accuracy: 84.4%, Validation Acc: 85.2% *
Iter: 200, Train-Batch Accuracy: 92.2%, Validation Acc: 91.5% *
Iter: 300, Train-Batch Accuracy: 95.3%, Validation Acc: 93.7% *
Iter: 400, Train-Batch Accuracy: 92.2%, Validation Acc: 94.3% *
Iter: 500, Train-Batch Accuracy: 98.4%, Validation Acc: 94.7% *
Iter: 600, Train-Batch Accuracy: 93.8%, Validation Acc: 94.7%
Iter: 700, Train-Batch Accuracy: 98.4%, Validation Acc: 95.6% *
Iter: 800, Train-Batch Accuracy: 100.0%, Validation Acc: 96.3% *
Iter: 900, Train-Batch Accuracy: 98.4%, Validation Acc: 96.4% *
Iter: 1000, Train-Batch Accuracy: 100.0%, Validation Acc: 96.9% *
Iter: 1100, Train-Batch Accuracy: 96.9%, Validation Acc: 97.0% *
Iter: 1200, Train-Batch Accuracy: 93.8%, Validation Acc: 97.0% *
Iter: 1300, Train-Batch Accuracy: 92.2%, Validation Acc: 97.2% *
Iter: 1400, Train-Batch Accuracy: 100.0%, Validation Acc: 97.3% *
Iter: 1500, Train-Batch Accuracy: 96.9%, Validation Acc: 97.4% *
Iter: 1600, Train-Batch Accuracy: 100.0%, Validation Acc: 97.7% *
Iter: 1700, Train-Batch Accuracy: 100.0%, Validation Acc: 97.8% *
Iter: 1800, Train-Batch Accuracy: 98.4%, Validation Acc: 97.7%
Iter: 1900, Train-Batch Accuracy: 98.4%, Validation Acc: 98.1% *
Iter: 2000, Train-Batch Accuracy: 95.3%, Validation Acc: 98.0%
Iter: 2100, Train-Batch Accuracy: 98.4%, Validation Acc: 97.9%
Iter: 2200, Train-Batch Accuracy: 100.0%, Validation Acc: 98.0%
Iter: 2300, Train-Batch Accuracy: 96.9%, Validation Acc: 98.1%
Iter: 2400, Train-Batch Accuracy: 93.8%, Validation Acc: 98.1%
Iter: 2500, Train-Batch Accuracy: 98.4%, Validation Acc: 98.2% *
Iter: 2600, Train-Batch Accuracy: 98.4%, Validation Acc: 98.0%
Iter: 2700, Train-Batch Accuracy: 98.4%, Validation Acc: 98.0%
Iter: 2800, Train-Batch Accuracy: 96.9%, Validation Acc: 98.1%
Iter: 2900, Train-Batch Accuracy: 96.9%, Validation Acc: 98.2%
Iter: 3000, Train-Batch Accuracy: 98.4%, Validation Acc: 98.2%
Iter: 3100, Train-Batch Accuracy: 100.0%, Validation Acc: 98.1%
Iter: 3200, Train-Batch Accuracy: 100.0%, Validation Acc: 98.3% *
Iter: 3300, Train-Batch Accuracy: 98.4%, Validation Acc: 98.4% *
Iter: 3400, Train-Batch Accuracy: 95.3%, Validation Acc: 98.0%
Iter: 3500, Train-Batch Accuracy: 98.4%, Validation Acc: 98.3%
Iter: 3600, Train-Batch Accuracy: 100.0%, Validation Acc: 98.5% *
Iter: 3700, Train-Batch Accuracy: 98.4%, Validation Acc: 98.3%
Iter: 3800, Train-Batch Accuracy: 96.9%, Validation Acc: 98.1%
Iter: 3900, Train-Batch Accuracy: 96.9%, Validation Acc: 98.5%
Iter: 4000, Train-Batch Accuracy: 100.0%, Validation Acc: 98.4%
Iter: 4100, Train-Batch Accuracy: 100.0%, Validation Acc: 98.5%
Iter: 4200, Train-Batch Accuracy: 100.0%, Validation Acc: 98.3%
Iter: 4300, Train-Batch Accuracy: 100.0%, Validation Acc: 98.6% *
Iter: 4400, Train-Batch Accuracy: 96.9%, Validation Acc: 98.4%
Iter: 4500, Train-Batch Accuracy: 98.4%, Validation Acc: 98.5%
Iter: 4600, Train-Batch Accuracy: 98.4%, Validation Acc: 98.5%
Iter: 4700, Train-Batch Accuracy: 98.4%, Validation Acc: 98.4%
Iter: 4800, Train-Batch Accuracy: 100.0%, Validation Acc: 98.8% *
Iter: 4900, Train-Batch Accuracy: 100.0%, Validation Acc: 98.8%
Iter: 5000, Train-Batch Accuracy: 98.4%, Validation Acc: 98.6%
Iter: 5100, Train-Batch Accuracy: 98.4%, Validation Acc: 98.6%
Iter: 5200, Train-Batch Accuracy: 100.0%, Validation Acc: 98.6%
Iter: 5300, Train-Batch Accuracy: 96.9%, Validation Acc: 98.5%
Iter: 5400, Train-Batch Accuracy: 98.4%, Validation Acc: 98.7%
Iter: 5500, Train-Batch Accuracy: 98.4%, Validation Acc: 98.6%
Iter: 5600, Train-Batch Accuracy: 100.0%, Validation Acc: 98.4%
Iter: 5700, Train-Batch Accuracy: 100.0%, Validation Acc: 98.6%
Iter: 5800, Train-Batch Accuracy: 100.0%, Validation Acc: 98.7%
No improvement found in a while, stopping optimization.
Time usage: 0:00:28
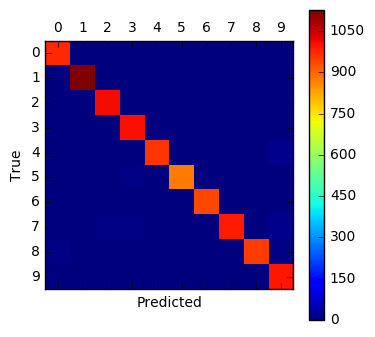
print_test_accuracy(show_example_errors=True,
show_confusion_matrix=True)
Accuracy on Test-Set: 98.4% (9842 / 10000)
Example errors:

Confusion Matrix:
[[ 974 0 0 0 0 1 2 0 2 1]
[ 0 1127 2 2 0 0 1 0 3 0]
[ 4 4 1012 4 1 0 0 3 4 0]
[ 0 0 1 1005 0 2 0 0 2 0]
[ 1 0 1 0 961 0 2 0 3 14]
[ 2 0 1 6 0 880 1 0 1 1]
[ 4 2 0 1 3 4 942 0 2 0]
[ 1 1 8 6 1 0 0 994 1 16]
[ 6 0 1 4 1 1 1 2 952 6]
[ 3 3 0 3 2 2 0 0 1 995]]
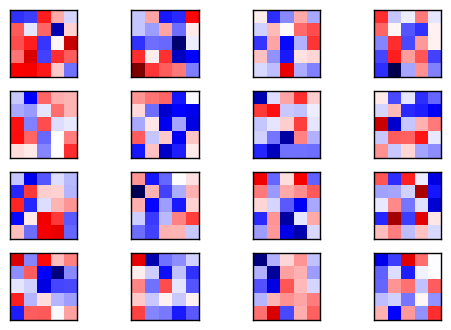
现在卷积权重是经过优化的。将这些与上面的随机权重进行对比。它们看起来基本相同。实际上,一开始我以为程序有bug,因为优化前后的权重看起来差不多。
但保存图像,并排着比较它们(你可以右键保存)。你会发现两者有细微的不同。
平均值和标准差也有一点变化,因此优化过的权重肯定是不一样的。
plot_conv_weights(weights=weights_conv1)
Mean: 0.02895, Stdev: 0.29949
再次初始化变量
再一次用随机值来初始化所有神经网络变量。
init_variables()
这意味着神经网络又是完全随机地对图片进行分类,由于只是随机的猜测所以分类准确率很低。
print_test_accuracy()
Accuracy on Test-Set: 13.4% (1341 / 10000)
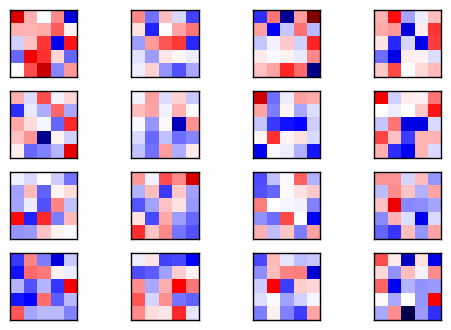
卷积权重看起来应该与上面的不同。
plot_conv_weights(weights=weights_conv1)
Mean: -0.01086, Stdev: 0.28023
恢复最好的变量
重新载入在优化过程中保存到文件的所有变量。
saver.restore(sess=session, save_path=save_path)
使用之前保存的那些变量,分类准确率又提高了。
注意,准确率与之前相比可能会有细微的上升或下降,这是由于文件里的变量是用来最大化验证集上的分类准确率,但在保存文件之后,又进行了1000次的优化迭代,因此这是两组有轻微不同的变量的结果。有时这会导致测试集上更好或更差的表现。
print_test_accuracy(show_example_errors=True,
show_confusion_matrix=True)
Accuracy on Test-Set: 98.3% (9826 / 10000)
Example errors:
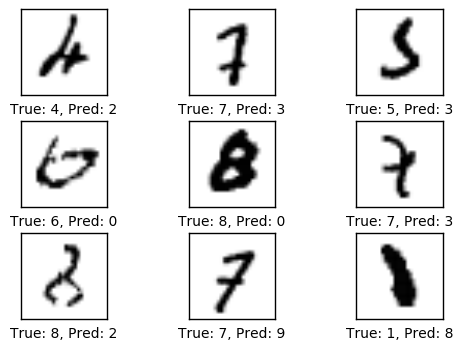
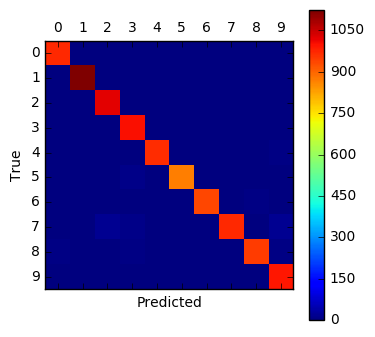
Confusion Matrix:
[[ 973 0 0 0 0 0 2 0 3 2]
[ 0 1124 2 2 0 0 3 0 4 0]
[ 2 1 1027 0 0 0 0 1 1 0]
[ 0 0 1 1005 0 2 0 0 2 0]
[ 0 0 3 0 968 0 1 0 3 7]
[ 2 0 1 9 0 871 3 0 3 3]
[ 4 2 1 0 3 3 939 0 6 0]
[ 1 3 19 11 2 0 0 972 2 18]
[ 6 0 3 5 1 0 1 2 951 5]
[ 3 3 0 1 4 1 0 0 1 996]]
卷积权重也与之前显示的图几乎相同,同样,由于多做了1000次优化迭代,二者并非完全一样。
plot_conv_weights(weights=weights_conv1)
Mean: 0.02792, Stdev: 0.29822
关闭TensorFlow会话
现在我们已经用TensorFlow完成了任务,关闭session,释放资源。
# This has been commented out in case you want to modify and experiment
# with the Notebook without having to restart it.
# session.close()
总结
这篇教程描述了在TensorFlow中如何保存并恢复神经网络的变量。它有许多用处。比如,当你用神经网络来识别图像的时候,只需要训练网络一次,然后可以在其他电脑上完成开发工作。
checkpoint的另一个用处是,如果你有一个非常大的神经网络和数据集,就可能会在中间保存一些checkpoints来避免电脑死机,这样,你就可以在最近的checkpoint开始优化而不是重头开始。
本教程也展示了如何用验证集来进行所谓的Early Stopping,如果没有降低验证错误优化就会终止。这在神经网络出现过拟合以及开始学习训练集中的噪声时很有用;不过这在本教程的神经网络和MNIST数据集中并不是什么大问题。
还有一个有趣的现象,最优化时卷积权重(或者叫滤波)的变化很小,即使网络的性能从随机猜测提高到近乎完美的分类。奇怪的是随机的权重好像已经足够好了。你认为为什么会有这种现象?
练习
下面使一些可能会让你提升TensorFlow技能的一些建议练习。为了学习如何更合适地使用TensorFlow,实践经验是很重要的。
在你对这个Notebook进行修改之前,可能需要先备份一下。
- 在经过1000次迭代而性能没有提升时,优化就终止了。这样够吗?你能想出一个更好地进行Early Stopping的方法么?试着实现它。
- 如果checkpoint文件已经存在了,载入它而不是做优化。
- 每100次优化迭代保存一次checkpoint。通过
saver.latest_checkpoint()取回最新的(保存点)。为什么保存多个checkpoints而不是只保存最近的一个? - 试着改变神经网络,比如添加其他层。当你从不同的网络中重新载入变量会出现什么问题?
- 用
plot_conv_weights()函数在优化前后画出第二个卷积层的权重。它们几乎相同的么? - 你认为优化过的卷积权重为什么与随机初始化的(权重)几乎相同?
- 不看源码,自己重写程序。
- 向朋友解释程序如何工作。
License (MIT)
Copyright (c) 2016 by Magnus Erik Hvass Pedersen
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.