第十七章 排序
译者:飞龙
自豪地采用谷歌翻译
计算机科学领域过度痴迷于排序算法。根据 CS 学生在这个主题上花费的时间,你会认为排序算法的选择是现代软件工程的基石。当然,现实是,软件开发人员可以在很多年中,或者整个职业生涯中,不必考虑排序如何工作。对于几乎所有的应用程序,它们都使用它们使用的语言或库提供的通用算法。通常这样就行了。
所以如果你跳过这一章,不了解排序算法,你仍然是一个优秀的开发人员。但是有一些原因你可能想要这样:
- 尽管有绝大多数应用程序都可以使用通用算法,但你可能需要了解两种专用算法:基数排序和有界堆排序。
- 一种排序算法,归并排序,是一个很好的教学示例,因为它演示了一个重要和实用的算法设计策略,称为“分治”。此外,当我们分析其表现时,你将了解到我们以前没有看到的增长级别,即线性对数。最后,一些最广泛使用的算法是包含归并排序的混合体。
- 了解排序算法的另一个原因是,技术面试官喜欢询问它们。如果你想要工作,如果你能展示 CS 文化素养,就有帮助。
因此,在本章中我们将分析插入排序,你将实现归并排序,我将给你讲解基数排序,你将编写有界堆排序的简单版本。
17.1 插入排序
我们将从插入排序开始,主要是因为它的描述和实现很简单。它不是很有效,但它有一些补救的特性,我们将看到它。
我们不在这里解释算法,建议你阅读 http://thinkdast.com/insertsort 中的插入排序的维基百科页面 ,其中包括伪代码和动画示例。当你理解了它的思路再回来。
这是 Java 中插入排序的实现:
public class ListSorter<T> {
public void insertionSort(List<T> list, Comparator<T> comparator) {
for (int i=1; i < list.size(); i++) {
T elt_i = list.get(i);
int j = i;
while (j > 0) {
T elt_j = list.get(j-1);
if (comparator.compare(elt_i, elt_j) >= 0) {
break;
}
list.set(j, elt_j);
j--;
}
list.set(j, elt_i);
}
}
}
我定义了一个类,ListSorter作为排序算法的容器。通过使用类型参数T,我们可以编写一个方法,它在包含任何对象类型的列表上工作。
insertionSort需要两个参数,一个是任何类型的List,一个是Comparator,它知道如何比较类型T的对象。它对列表“原地”排序,这意味着它修改现有列表,不必分配任何新空间。
下面的示例演示了,如何使用Integer的List对象,调用此方法:
List<Integer> list = new ArrayList<Integer>(
Arrays.asList(3, 5, 1, 4, 2));
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer elt1, Integer elt2) {
return elt1.compareTo(elt2);
}
};
ListSorter<Integer> sorter = new ListSorter<Integer>();
sorter.insertionSort(list, comparator);
System.out.println(list);
insertionSort有两个嵌套循环,所以你可能会猜到,它的运行时间是二次的。在这种情况下,一般是正确的,但你做出这个结论之前,你必须检查,每个循环的运行次数与n,数组的大小成正比。
外部循环从1迭代到list.size(),因此对于列表的大小n是线性的。内循环从i迭代到0,所以在n中也是线性的。因此,两个循环运行的总次数是二次的。
如果你不确定,这里是证明:
第一次循环中,i = 1,内循环最多运行一次。
第二次,i = 2,内循环最多运行两次。
最后一次,i = n - 1,内循环最多运行n次。
因此,内循环运行的总次数是序列1, 2, ..., n - 1的和,即n(n - 1)/2。该表达式的主项(拥有最高指数)为n^2。
在最坏的情况下,插入排序是二次的。然而:
- 如果这些元素已经有序,或者几乎这样,插入排序是线性的。具体来说,如果每个元素距离它的有序位置不超过
k个元素,则内部循环不会运行超过k次,并且总运行时间是O(kn)。 - 由于实现简单,开销较低;也就是,尽管运行时间是
an^2,主项的系数a,也可能是小的。
所以如果我们知道数组几乎是有序的,或者不是很大,插入排序可能是一个不错的选择。但是对于大数组,我们可以做得更好。其实要好很多。
17.2 练习 14
归并排序是运行时间优于二次的几种算法之一。同样,不在这里解释算法,我建议你阅读维基百科 http://thinkdast.com/mergesort。一旦你有了想法,反回来,你可以通过写一个实现来测试你的理解。
在本书的仓库中,你将找到此练习的源文件:
ListSorter.javaListSorterTest.java
运行ant build来编译源文件,然后运行ant ListSorterTest。像往常一样,它应该失败,因为你有工作要做。
在ListSorter.java中,我提供了两个方法的大纲,mergeSortInPlace以及mergeSort:
public void mergeSortInPlace(List<T> list, Comparator<T> comparator) {
List<T> sorted = mergeSortHelper(list, comparator);
list.clear();
list.addAll(sorted);
}
private List<T> mergeSort(List<T> list, Comparator<T> comparator) {
// TODO: fill this in!
return null;
}
这两种方法做同样的事情,但提供不同的接口。mergeSort获取一个列表,并返回一个新列表,具有升序排列的相同元素。mergeSortInPlace是修改现有列表的void方法。
你的工作是填充mergeSort。在编写完全递归版本的合并排序之前,首先要这样:
- 将列表分成两半。
- 使用
Collections.sort或insertionSort来排序这两部分。 - 将有序的两部分合并为一个完整的有序列表中。
这将给你一个机会来调试用于合并的代码,而无需处理递归方法的复杂性。
接下来,添加一个边界情况(请参阅 < http://thinkdast.com/basecase> )。如果你只提供一个列表,仅包含一个元素,则可以立即返回,因为它已经有序。或者如果列表的长度低于某个阈值,则可以使用Collections.sort或insertionSort。在进行前测试边界情况。
最后,修改你的解决方案,使其进行两次递归调用来排序数组的两个部分。当你使其正常工作,testMergeSort和testMergeSortInPlace应该通过。
17.3 归并排序的分析
为了对归并排序的运行时间进行划分,对递归层级和每个层级上完成多少工作方面进行思考,是很有帮助的。假设我们从包含n个元素的列表开始。以下是算法的步骤:
- 生成两个新数组,并将一半元素复制到每个数组中。
- 排序两个数组。
- 合并两个数组。
图 17.1 显示了这些步骤。
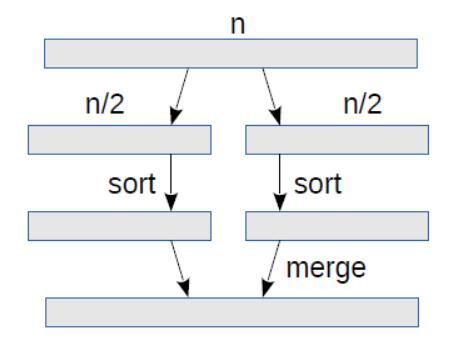
图 17.1:归并排序的展示,它展示了递归的一个层级。
第一步复制每个元素一次,因此它是线性的。第三步也复制每个元素一次,因此它也是线性的。现在我们需要弄清楚步骤2的复杂性。为了做到这一点,查看不同的计算图片会有帮助,它展示了递归的层数,如图 17.2 所示。
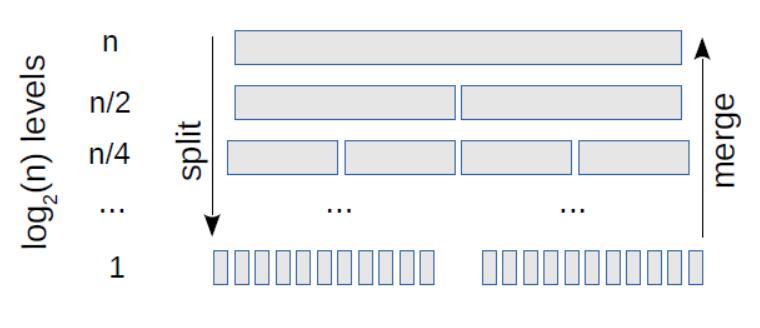
图 17.2:归并排序的展示,它展示了递归的所有层级。
在顶层,我们有1个列表,其中包含n个元素。为了简单起见,我们假设n是2的幂。在下一层,有2个列表包含n/2个元素。然后是4个列表与n/4元素,以此类推,直到我们得到n个列表与1元素。
在每一层,我们共有n个元素。在下降的过程中,我们必须将数组分成两半,这在每一层上都需要与n成正比的时间。在回来的路上,我们必须合并n个元素,这也是线性的。
如果层数为h,算法的总工作量为O(nh)。那么有多少层呢?有两种方法可以考虑:
- 我们用多少步,可以将
n减半直到1? - 或者,我们用多少步,可以将
1加倍直到n?
第二个问题的另一种形式是“2的多少次方是n”?
2^h = n
对两边取以2为底的对数:
h = log2(n)
所以总时间是O(nlogn)。我没有纠结于对数的底,因为底不同的对数差别在于一个常数,所以所有的对数都是相同的增长级别。
O(nlogn)中的算法有时被称为“线性对数”的,但大多数人只是说n log n。
事实证明,O(nlogn)是通过元素比较的排序算法的理论下限。这意味着没有任何“比较排序”的增长级别比n log n好。请参见 http://thinkdast.com/compsort。
但是我们将在下一节中看到,存在线性时间的非比较排序!
基数排序
在 2008 年美国总统竞选期间,候选人巴拉克·奥巴马在访问 Google 时,被要求进行即兴算法分析。首席执行长埃里克·施密特开玩笑地问他,“排序一百万个 32 位整数的最有效的方法”。显然有人暗中告诉了奥巴马,因为他很快就回答说:“我认为冒泡排序是错误的。”你可以在 http://thinkdast.com/obama 观看视频。
奥巴马是对的:冒泡排序在概念上是简单的,但其运行时间是二次的; 即使在二次排序算法中,其性能也不是很好。见 http://thinkdast.com/bubble。
施密特想要的答案可能是“基数排序”,这是一种非比较排序算法,如果元素的大小是有界的,例如 32 位整数或 20 个字符的字符串,它就可以工作。
为了看看它是如何工作的,想象你有一堆索引卡,每张卡片包含三个字母的单词。以下是一个方法,可以对卡进行排序:
- 根据第一个字母,将卡片放入桶中。所以以
a开头的单词应该在一个桶中,其次是以b开头的单词,以此类推 - 根据第二个字母再次将卡片放入每个桶。所以以
aa开头的应该在一起,其次是以ab开头的,以此类推当然,并不是所有的桶都是满的,但是没关系。 - 根据第三个字母再次将卡片放入每个桶。
此时,每个桶包含一个元素,桶按升序排列。图 17.3 展示了三个字母的例子。

图 17.3:三个字母的基数排序的例子
最上面那行显示未排序的单词。第二行显示第一次遍历后的桶的样子。每个桶中的单词都以相同的字母开头。
第二遍之后,每个桶中的单词以相同的两个字母开头。在第三遍之后,每个桶中只能有一个单词,并且桶是有序的。
在每次遍历期间,我们遍历元素并将它们添加到桶中。只要桶允许在恒定时间内添加元素,每次遍历是线性的。
遍历数量,我会称之为w,取决于单词的“宽度”,但不取决于单词的数量,n。所以增长级别是O(wn),对于n是线性的。
基数排序有许多变体,并有许多方法来实现每一个。你可以在 http://thinkdast.com/radix 上阅读他们的更多信息。作为一个可选的练习,请考虑编写基数排序的一个版本。
17.5 堆排序
基数排序适用于大小有界的东西,除了他之外,还有一种你可能遇到的其它专用排序算法:有界堆排序。如果你在处理非常大的数据集,你想要得到前 10 个或者前k个元素,其中k远小于n,它是很有用的。
例如,假设你正在监视一 个Web 服务,它每天处理十亿次事务。在每一天结束时,你要汇报最大的k个事务(或最慢的,或者其它最 xx 的)。一个选项是存储所有事务,在一天结束时对它们进行排序,然后选择最大的k个。需要的时间与nlogn成正比,这非常慢,因为我们可能无法将十亿次交易记录在单个程序的内存中。我们必须使用“外部”排序算法。你可以在 http://thinkdast.com/extsort 上了解外部排序。
使用有界堆,我们可以做得更好!以下是我们的实现方式:
- 我会解释(无界)堆排序。
- 你会实现它
- 我将解释有界堆排序并进行分析。
要了解堆排序,你必须了解堆,这是一个类似于二叉搜索树(BST)的数据结构。有一些区别:
- 在 BST 中,每个节点
x都有“BST 特性”:x左子树中的所有节点都小于x,右子树中的所有节点都大于x。 - 在堆中,每个节点
x都有“堆特性”:两个子树中的所有节点都大于x。 - 堆就像平衡的 BST;当你添加或删除元素时,他们会做一些额外的工作来重新使树平衡。因此,可以使用元素的数组来有效地实现它们。
译者注:这里先讨论最小堆。如果子树中所有节点都小于
x,那么就是最大堆。
堆中最小的元素总是在根节点,所以我们可以在常数时间内找到它。在堆中添加和删除元素需要的时间与树的高度h成正比。而且由于堆总是平衡的,所以h与log n成正比。你可以在 http://thinkdast.com/heap 上阅读更多堆的信息。
JavaPriorityQueue使用堆实现。PriorityQueue提供Queue接口中指定的方法,包括offer和poll:
offer:将一个元素添加到队列中,更新堆,使每个节点都具有“堆特性”。需要logn的时间。poll:从根节点中删除队列中的最小元素,并更新堆。需要logn的时间。
给定一个PriorityQueue,你可以像这样轻松地排序的n个元素的集合 :
- 使用
offer,将集合的所有元素添加到PriorityQueue。 - 使用
poll从队列中删除元素并将其添加到List。
因为poll返回队列中剩余的最小元素,所以元素按升序添加到List。这种排序方式称为堆排序 (请参阅 http://thinkdast.com/heapsort)。
向队列中添加n个元素需要nlogn的时间。删除n个元素也是如此。所以堆排序的运行时间是O(n logn)。
在本书的仓库中,你可以在ListSorter.java中找到heapSort方法的大纲。填充它,然后运行ant ListSorterTest来确认它可以工作。
17.6 有界堆排序
有界堆是一个限制为最多包含k个元素的堆。如果你有n个元素,你可以跟踪这个最大的k个元素:
最初堆是空的。对于每个元素x:
- 分支 1:如果堆不满,请添加
x到堆中。 - 分支 2:如果堆满了,请与堆中
x的最小元素进行比较。如果x较小,它不能是最大的k个元素之一,所以你可以丢弃它。 - 分支 3:如果堆满了,并且
x大于堆中的最小元素,请从堆中删除最小的元素并添加x。
使用顶部为最小元素的堆,我们可以跟踪最大的k个元素。我们来分析这个算法的性能。对于每个元素,我们执行以下操作之一:
- 分支 1:将元素添加到堆是
O(log k)。 - 分支 2:找到堆中最小的元素是
O(1)。 - 分支 3:删除最小元素是
O(log k)。添加x也是O(log k)。
在最坏的情况下,如果元素按升序出现,我们总是执行分支 3。在这种情况下,处理n个元素的总时间是O(n log k),对于n是线性的。
在ListSorter.java中,你会发现一个叫做topK的方法的大纲,它接受一个List、Comparator和一个整数k。它应该按升序返回List的k个最大的元素 。填充它,然后运行ant ListSorterTest来确认它可以工作。
17.7 空间复杂性
到目前为止,我们已经谈到了很多运行时间的分析,但是对于许多算法,我们也关心空间。例如,归并排序的一个缺点是它会复制数据。在我们的实现中,它分配的空间总量是O(n log n)。通过更机智的实现,你可以将空间要求降至O(n)。
相比之下,插入排序不会复制数据,因为它会原地排序元素。它使用临时变量来一次性比较两个元素,并使用一些其它局部变量。但它的空间使用不取决于n。
我们的堆排序实现创建了新PriorityQueue,来存储元素,所以空间是O(n); 但是如果你能够原地对列表排序,则可以使用O(1)的空间执行堆排序 。
刚刚实现的有界堆栈算法的一个好处是,它只需要与k成正比的空间(我们要保留的元素的数量),而k通常比n小得多 。
软件开发人员往往比空间更加注重运行时间,对于许多应用程序来说,这是适当的。但是对于大型数据集,空间可能同等或更加重要。例如:
- 如果一个数据集不能放入一个程序的内存,那么运行时间通常会大大增加,或者根本不能运行。如果你选择一个需要较少空间的算法,并且这样可以将计算放入内存中,则可能会运行得更快。同样,使用较少空间的程序,可能会更好地利用 CPU 缓存并运行速度更快(请参阅 http://thinkdast.com/cache)。
- 在同时运行多个程序的服务器上,如果可以减少每个程序所需的空间,则可以在同一台服务器上运行更多程序,从而降低硬件和能源成本。
所以这些是一些原因,你应该至少了解一些算法的空间需求。