六、使用鲁棒回归的 CT 扫描的压缩感知
广播
术语广播描述了在算术运算期间,如何处理不同形状的数组。 Numpy 首先使用广播一词,但现在用于其他库,如 Tensorflow 和 Matlab;规则因库而异。
来自 Numpy 文档:
广播提供了一种向量化数组操作的方法,使循环在 C 而不是 Python 中出现。 它可以不制作不必要的数据副本而实现,并且通常可以产生高效实现。最简单的广播示例在数组乘以标量时发生。
a = np.array([1.0, 2.0, 3.0])
b = 2.0
a * b
# array([ 2., 4., 6.])
v=np.array([1,2,3])
print(v, v.shape)
# [1 2 3] (3,)
m=np.array([v,v*2,v*3]); m, m.shape
'''
(array([[1, 2, 3],
[2, 4, 6],
[3, 6, 9]]), (3, 3))
'''
n = np.array([m*1, m*5])
n
'''
array([[[ 1, 2, 3],
[ 2, 4, 6],
[ 3, 6, 9]],
[[ 5, 10, 15],
[10, 20, 30],
[15, 30, 45]]])
'''
n.shape, m.shape
# ((2, 3, 3), (3, 3))
我们可以使用广播来将矩阵和数组相加:
m+v
'''
array([[ 2, 4, 6],
[ 3, 6, 9],
[ 4, 8, 12]])
'''
注意如果我们转置数组会发生什么:
v1=np.expand_dims(v,-1); v1, v1.shape
'''
(array([[1],
[2],
[3]]), (3, 1))
'''
m+v1
'''
array([[ 2, 3, 4],
[ 4, 6, 8],
[ 6, 9, 12]])
'''
通用的 NumPy 广播规则
操作两个数组时,NumPy 会逐元素地比较它们的形状。 它从最后的维度开始,并向前移动。 如果满足:
- 他们是相等的,或者
- 其中一个是 1
两个维度兼容。
数组不需要具有相同数量的维度。 例如,如果你有一个256×256×3的 RGB 值数组,并且你希望将图像中的每种颜色缩放不同的值,则可以将图像乘以具有 3 个值的一维数组。 根据广播规则排列这些数组的尾部轴的大小,表明它们是兼容的:
Image (3d array): 256 x 256 x 3
Scale (1d array): 3
Result (3d array): 256 x 256 x 3
回顾
v = np.array([1,2,3,4])
m = np.array([v,v*2,v*3])
A = np.array([5*m, -1*m])
v.shape, m.shape, A.shape
# ((4,), (3, 4), (2, 3, 4))
下列操作有效嘛?
A
A + v
A.T + v
A.T.shape
(SciPy 中的)稀疏矩阵
具有大量零的矩阵称为稀疏(稀疏是密集的反义)。 对于稀疏矩阵,仅仅存储非零值,可以节省大量内存。

另一个大型稀疏矩阵的例子:
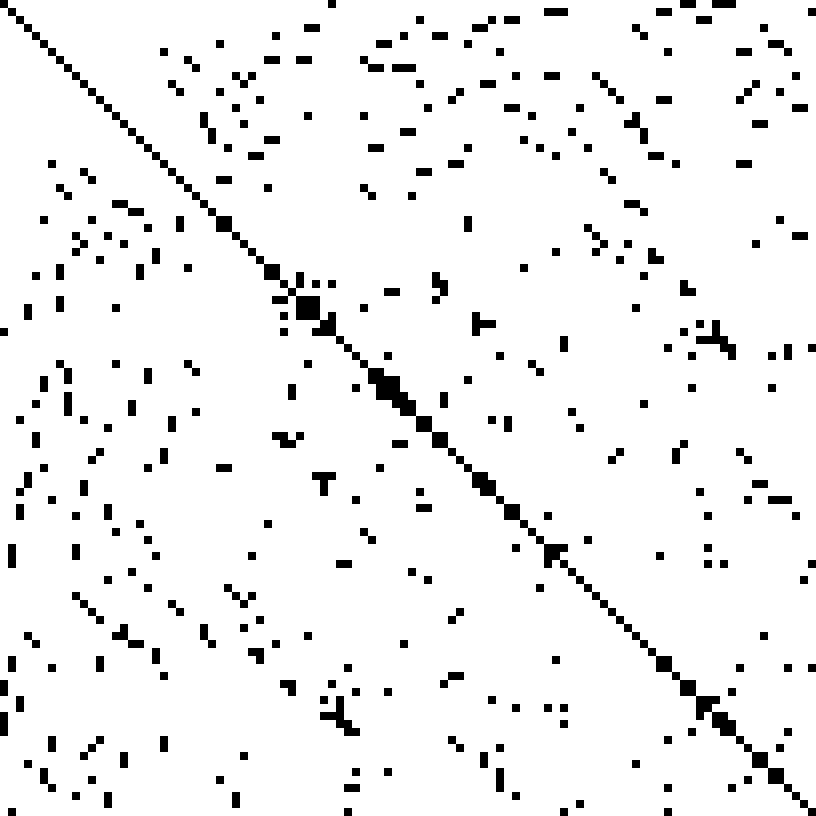
这是最常见的稀疏存储格式:
- 逐坐标(scipy 称 COO)
- 压缩稀疏行(CSR)
- 压缩稀疏列(CSC)
让我们来看看这些例子。
实际上还有更多格式。
如果非零元素的数量与行(或列)的数量成比例而不是与行列的乘积成比例,则通常将一类矩阵(例如,对角)称为稀疏。
Scipy 实现
来自 Scipy 稀疏矩阵文档
- 为了有效地构造矩阵,请使用
dok_matrix或lil_matrix。lil_matrix类支持基本切片和花式索引,其语法与 NumPy 数组类似。 如下所示,COO 格式也可用于有效地构造矩阵 - 要执行乘法或求逆等操作,首先要将矩阵转换为 CSC 或 CSR 格式。
- CSR,CSC 和 COO 格式之间的所有转换都是高效的线性时间操作。
今天:CT 扫描
引言
“数学真的可以拯救你的生命吗?当然可以!!” (可爱的文章)
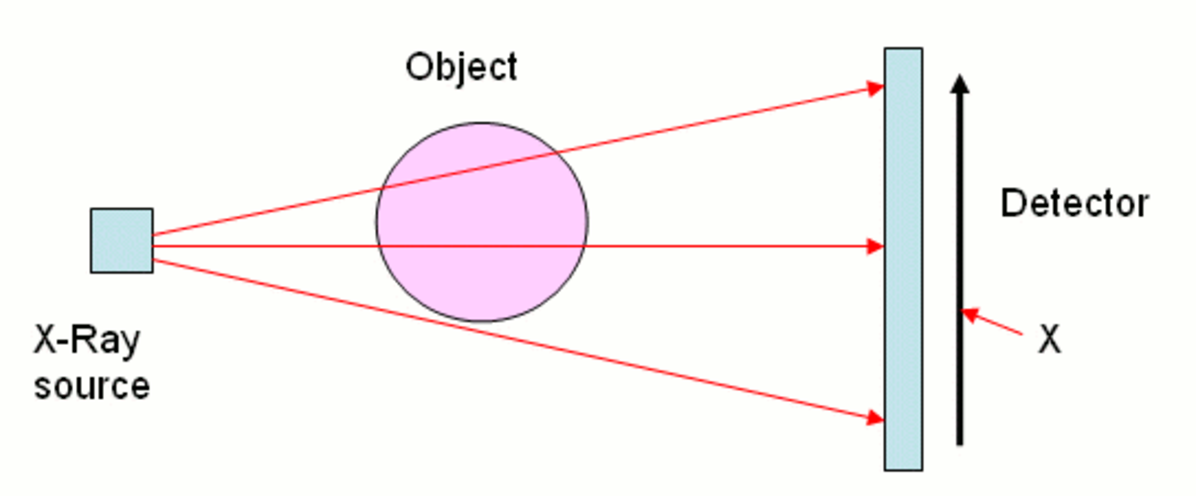
(CAT 和 CT 扫描指代相同的过程。CT 扫描是更现代的术语)
本课程基于 Scikit-Learn 示例压缩感知:使用 L1 先验的层析成像重建(Lasso)。
我们今天的目标
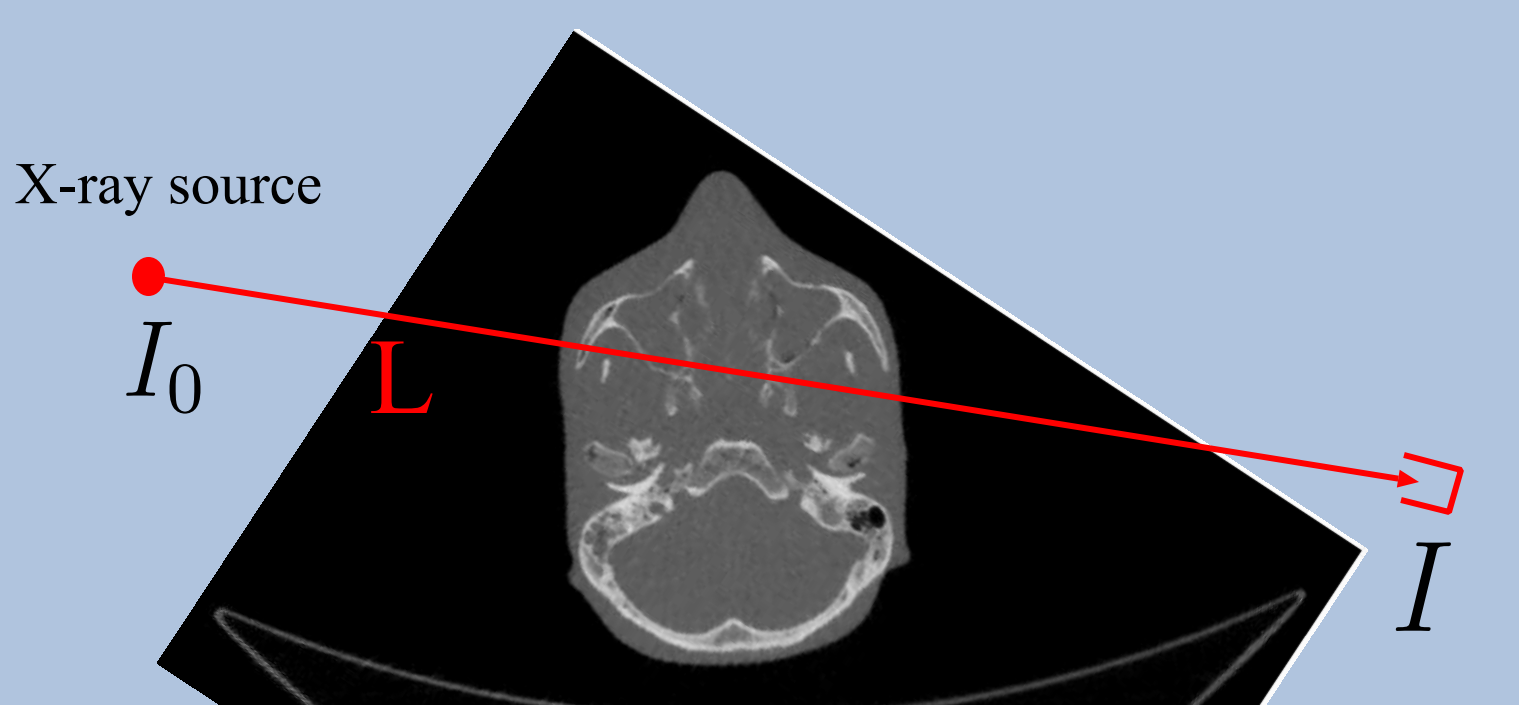
读取 CT 扫描的结果并构建原始图像。

对于(特定位置和特定角度的)每个 X 射线,我们进行单次测量。 我们需要从这些测量中构建原始图像。 此外,我们不希望患者经历大量辐射,因此我们收集的数据少于图片区域。

我们会看到:
来源:压缩感知
导入
%matplotlib inline
import numpy as np, matplotlib.pyplot as plt, math
from scipy import ndimage, sparse
np.set_printoptions(suppress=True)
生成数据
引言
我们将使用生成的数据(不是真正的 CT 扫描)。 生成数据涉及一些有趣的 numpy 和线性代数,我们稍后会再回过头来看。
代码来自 Scikit-Learn 示例压缩感知:使用 L1 先验的层析成像重建(Lasso)。
生成图像
def generate_synthetic_data():
rs = np.random.RandomState(0)
n_pts = 36
x, y = np.ogrid[0:l, 0:l]
mask_outer = (x - l / 2) ** 2 + (y - l / 2) ** 2 < (l / 2) ** 2
mx,my = rs.randint(0, l, (2,n_pts))
mask = np.zeros((l, l))
mask[mx,my] = 1
mask = ndimage.gaussian_filter(mask, sigma=l / n_pts)
res = (mask > mask.mean()) & mask_outer
return res ^ ndimage.binary_erosion(res)
l = 128
data = generate_synthetic_data()
plt.figure(figsize=(5,5))
plt.imshow(data, cmap=plt.cm.gray);

generate_synthetic_data在做什么
l=8; n_pts=5
rs = np.random.RandomState(0)
x, y = np.ogrid[0:l, 0:l]; x,y
'''
(array([[0],
[1],
[2],
[3],
[4],
[5],
[6],
[7]]), array([[0, 1, 2, 3, 4, 5, 6, 7]]))
'''
x + y
'''
array([[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 1, 2, 3, 4, 5, 6, 7, 8],
[ 2, 3, 4, 5, 6, 7, 8, 9],
[ 3, 4, 5, 6, 7, 8, 9, 10],
[ 4, 5, 6, 7, 8, 9, 10, 11],
[ 5, 6, 7, 8, 9, 10, 11, 12],
[ 6, 7, 8, 9, 10, 11, 12, 13],
[ 7, 8, 9, 10, 11, 12, 13, 14]])
'''
(x - l/2) ** 2
'''
array([[ 16.],
[ 9.],
[ 4.],
[ 1.],
[ 0.],
[ 1.],
[ 4.],
[ 9.]])
'''
(x - l/2) ** 2 + (y - l/2) ** 2
'''
array([[ 32., 25., 20., 17., 16., 17., 20., 25.],
[ 25., 18., 13., 10., 9., 10., 13., 18.],
[ 20., 13., 8., 5., 4., 5., 8., 13.],
[ 17., 10., 5., 2., 1., 2., 5., 10.],
[ 16., 9., 4., 1., 0., 1., 4., 9.],
[ 17., 10., 5., 2., 1., 2., 5., 10.],
[ 20., 13., 8., 5., 4., 5., 8., 13.],
[ 25., 18., 13., 10., 9., 10., 13., 18.]])
'''
mask_outer = (x - l/2) ** 2 + (y - l/2) ** 2 < (l/2) ** 2; mask_outer
'''
array([[False, False, False, False, False, False, False, False],
[False, False, True, True, True, True, True, False],
[False, True, True, True, True, True, True, True],
[False, True, True, True, True, True, True, True],
[False, True, True, True, True, True, True, True],
[False, True, True, True, True, True, True, True],
[False, True, True, True, True, True, True, True],
[False, False, True, True, True, True, True, False]], dtype=bool)
'''
plt.imshow(mask_outer, cmap='gray')
# <matplotlib.image.AxesImage at 0x7efcd9303278>

mask = np.zeros((l, l))
mx,my = rs.randint(0, l, (2,n_pts))
mask[mx,my] = 1; mask
'''
array([[ 0., 1., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 1.],
[ 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 0., 0., 0., 0.]])
'''
plt.imshow(mask, cmap='gray')
# <matplotlib.image.AxesImage at 0x7efcd9293940>

mask = ndimage.gaussian_filter(mask, sigma=l / n_pts)
plt.imshow(mask, cmap='gray')
# <matplotlib.image.AxesImage at 0x7efcd922c0b8>

res = np.logical_and(mask > mask.mean(), mask_outer)
plt.imshow(res, cmap='gray');

plt.imshow(ndimage.binary_erosion(res), cmap='gray');
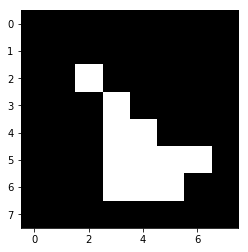
plt.imshow(res ^ ndimage.binary_erosion(res), cmap='gray');

生成投影
代码
def _weights(x, dx=1, orig=0):
x = np.ravel(x)
floor_x = np.floor((x - orig) / dx)
alpha = (x - orig - floor_x * dx) / dx
return np.hstack((floor_x, floor_x + 1)), np.hstack((1 - alpha, alpha))
def _generate_center_coordinates(l_x):
X, Y = np.mgrid[:l_x, :l_x].astype(np.float64)
center = l_x / 2.
X += 0.5 - center
Y += 0.5 - center
return X, Y
def build_projection_operator(l_x, n_dir):
X, Y = _generate_center_coordinates(l_x)
angles = np.linspace(0, np.pi, n_dir, endpoint=False)
data_inds, weights, camera_inds = [], [], []
data_unravel_indices = np.arange(l_x ** 2)
data_unravel_indices = np.hstack((data_unravel_indices,
data_unravel_indices))
for i, angle in enumerate(angles):
Xrot = np.cos(angle) * X - np.sin(angle) * Y
inds, w = _weights(Xrot, dx=1, orig=X.min())
mask = (inds >= 0) & (inds < l_x)
weights += list(w[mask])
camera_inds += list(inds[mask] + i * l_x)
data_inds += list(data_unravel_indices[mask])
proj_operator = sparse.coo_matrix((weights, (camera_inds, data_inds)))
return proj_operator
投影运算符
l = 128
proj_operator = build_projection_operator(l, l // 7)
proj_operator
'''
<2304x16384 sparse matrix of type '<class 'numpy.float64'>'
with 555378 stored elements in COOrdinate format>
'''
维度:角度(l // 7),位置(l),每个图像(l x l)
proj_t = np.reshape(proj_operator.todense().A, (l//7,l,l,l))
第一个坐标指的是线的角度,第二个坐标指代线的位置。
索引为 3 的角度的直线:
plt.imshow(proj_t[3,0], cmap='gray');

plt.imshow(proj_t[3,1], cmap='gray');

plt.imshow(proj_t[3,2], cmap='gray');

plt.imshow(proj_t[3,40], cmap='gray');

垂直位置 40 处的其他直线:
plt.imshow(proj_t[4,40], cmap='gray');

plt.imshow(proj_t[15,40], cmap='gray');

plt.imshow(proj_t[17,40], cmap='gray');

X 射线和数据之间的交点
接下来,我们想看看直线如何与我们的数据相交。 请记住,这就是数据的样子:
plt.figure(figsize=(5,5))
plt.imshow(data, cmap=plt.cm.gray)
plt.axis('off')
plt.savefig("images/data.png")

proj = proj_operator @ data.ravel()[:, np.newaxis]
角度为 17,位置为 40 的穿过数据的 X 射线:
plt.figure(figsize=(5,5))
plt.imshow(data + proj_t[17,40], cmap=plt.cm.gray)
plt.axis('off')
plt.savefig("images/data_xray.png")
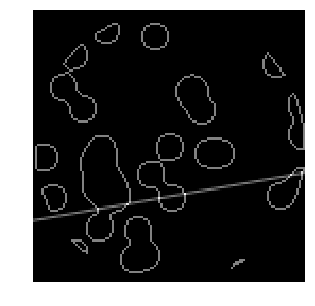
它们相交的地方。
both = data + proj_t[17,40]
plt.imshow((both > 1.1).astype(int), cmap=plt.cm.gray);

那条 X 射线的强度:
np.resize(proj, (l//7,l))[17,40]
# 6.4384498372605989
角度为 3,位置为 14 的穿过数据的 X 射线:
plt.imshow(data + proj_t[3,14], cmap=plt.cm.gray);
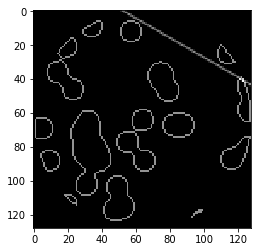
它们相交的地方。
both = data + proj_t[3,14]
plt.imshow((both > 1.1).astype(int), cmap=plt.cm.gray);

CT 扫描的测量结果在这里是一个小数字:
np.resize(proj, (l//7,l))[3,14]
# 2.1374953737965541
proj += 0.15 * np.random.randn(*proj.shape)
关于*args
a = [1,2,3]
b = [4,5,6]
c = list(zip(a, b))
c
# [(1, 4), (2, 5), (3, 6)]
list(zip(*c))
# [(1, 2, 3), (4, 5, 6)]
投影(CT 读取)
plt.figure(figsize=(7,7))
plt.imshow(np.resize(proj, (l//7,l)), cmap='gray')
plt.axis('off')
plt.savefig("images/proj.png")

回归
现在我们将尝试仅从投影中恢复数据(CT 扫描的测量值)。
线性回归:Xβ=y
我们的矩阵A是投影算子。 这是我们不同 X 射线上方的 4d 矩阵(角度,位置,x,y):
plt.figure(figsize=(12,12))
plt.title("X: Projection Operator")
plt.imshow(proj_operator.todense().A, cmap='gray')
# <matplotlib.image.AxesImage at 0x7efcd414ed30>

我们正在求解原始数据x。 我们将 2D 数据展开为单个列。
plt.figure(figsize=(5,5))
plt.title("beta: Image")
plt.imshow(data, cmap='gray')
plt.figure(figsize=(4,12))
# 我正在平铺列,使其更容易看到
plt.imshow(np.tile(data.ravel(), (80,1)).T, cmap='gray')
# <matplotlib.image.AxesImage at 0x7efcd3b1e278>


我们的向量y是展开的测量值矩阵:
plt.figure(figsize=(8,8))
plt.imshow(np.resize(proj, (l//7,l)), cmap='gray')
plt.figure(figsize=(10,10))
plt.imshow(np.tile(proj.ravel(), (20,1)).T, cmap='gray')
# <matplotlib.image.AxesImage at 0x7efcd34f8710>


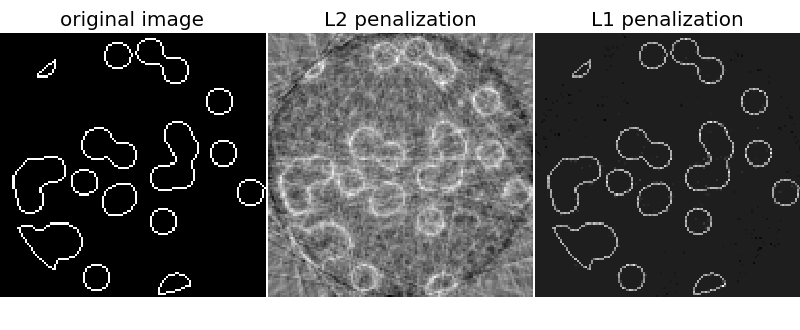
使用 Sklearn 线性回归重构图像
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
# 用 L2(岭)惩罚重建
rgr_ridge = Ridge(alpha=0.2)
rgr_ridge.fit(proj_operator, proj.ravel())
rec_l2 = rgr_ridge.coef_.reshape(l, l)
plt.imshow(rec_l2, cmap='gray')
# <matplotlib.image.AxesImage at 0x7efcd453d5c0>

18*128
# 2304
18 x 128 x 128 x 128
L1 范数产生稀疏性
单位球  在 L1 范数中是菱形。 它的极值是角:
在 L1 范数中是菱形。 它的极值是角:
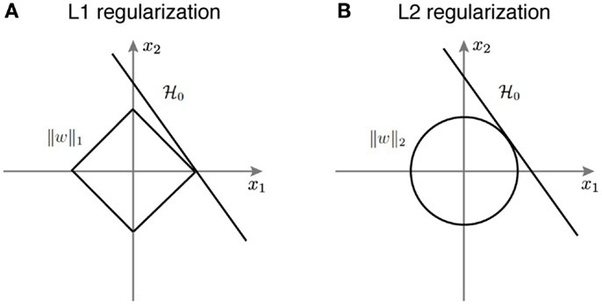
类似的视角是看损失函数的轮廓:
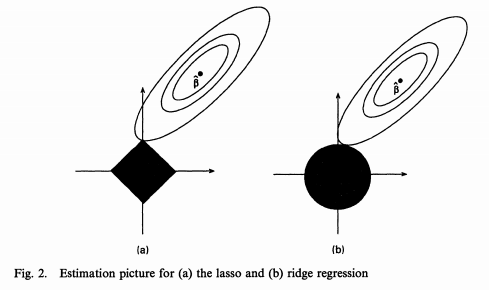
 是 L1 范数。 最小化 L1 范数会产生稀疏值。 对于矩阵,L1 范数等于最大绝对列范数。
是 L1 范数。 最小化 L1 范数会产生稀疏值。 对于矩阵,L1 范数等于最大绝对列范数。
 是核范数,它是奇异值的 L1 范数。 试图最小化它会产生稀疏的奇异值 -> 低秩。
是核范数,它是奇异值的 L1 范数。 试图最小化它会产生稀疏的奇异值 -> 低秩。
proj_operator.shape
# (2304, 16384)
# 使用 L1(Lasso)惩罚重建 α 的最佳值
# 使用 LassoCV 交叉验证来确定
rgr_lasso = Lasso(alpha=0.001)
rgr_lasso.fit(proj_operator, proj.ravel())
rec_l1 = rgr_lasso.coef_.reshape(l, l)
plt.imshow(rec_l1, cmap='gray')
# <matplotlib.image.AxesImage at 0x7efcd4919cf8>
这里的 L1 惩罚明显优于 L2 惩罚!