十四、线性模型
译者:飞龙
线性(回归)建模是一种方法,将输出值预测为输入值的加权线性组合。
线性模型 - 概述
在最简单的情况下,我们试图拟合一条线,因此我们的模型具有以下形式:
y = ax + b
在上面的这个等式中,我们试图从一些其他数据变量x预测一些数据变量y,其中和b是参数,我们需要通过拟合模型得出,并分别反映 模型(直线)的斜率和y`轴截距。
我们需要一些过程来寻找a和b。 我们将使用 OLS 这样做 - 我们想要的a和b的值是那些满足 OLS 解的值 - 也就是使模型预测与我们的数据之间距离最小的值。
请注意,你需要x和y已知的数据,以便训练你的模型。
该方法也可以推广,包括例如使用更多特征来预测我们感兴趣的输出。
因此,我们将以一般形式重写我们的模型,如下所示:
y = a0 + a1 x1 + a2 x2 + ... + an xn + ε
在上面的等式中,a0是截距(与上面的b相同),a1到an是我们正在尝试学习的n个参数,因为数据的权重为x1到xn。我们的输出变量(我们试图预测的)仍然是y,我们引入了ε,这是误差,它基本上捕获了无法解释的变动。
线性模型实战
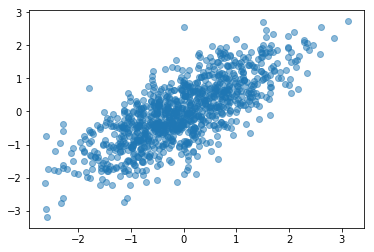
在下文中,我们将生成一些数据,其中两个特征D1和D2是相关的。
鉴于相关性,我们可以尝试从D1预测D2的值,我们将创建一个线性模型来实现。
使用上面第二种表示法,模型将采用以下形式:
D2 = a0 + a1 * D1
# 导入
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Statmodels & patsy
import patsy
import statsmodels.api as sm
# 生成一些互相关数据
# 设置
corr = 0.75
covs = [[1, corr], [corr, 1]]
means = [0, 0]
# 生成数据
dat = np.random.multivariate_normal(means, covs, 1000)
# 查看我们生成的数据
plt.scatter(dat[:, 0], dat[:, 1], alpha=0.5);
#plt.scatter(dat[:, 0], dat[:, 1], alpha=0.5);
# 将数据放入 DataFrame
df = pd.DataFrame(dat, columns=['D1', 'D2'])
# 观察数据
df.head()
| D1 | D2 | |
|---|---|---|
| 0 | 0.305994 | 0.521119 |
| 1 | 0.262456 | 0.562350 |
| 2 | -0.289970 | 0.608496 |
| 3 | 0.025279 | 0.523315 |
| 4 | -0.561126 | -1.320507 |
# 检查 D1 和 D2 之间的相关性(它与合成的东西匹配)
df.corr()
| D1 | D2 | |
|---|---|---|
| D1 | 1.000000 | 0.747094 |
| D2 | 0.747094 | 1.000000 |
Statsmodels & Patsy 的线性模型
Statsmodels 是 Python 中统计分析的模块。 Patsy 是一个有用的包,用于处理和描述统计模型。
这里是 statsmodels 和 patsy 的官方文档。
# Patsy 为我们提供了一种构建设计矩阵的简便方法
# 出于我们的目的,“设计矩阵”只是我们的预测变量和输出变量的有组织矩阵
outcome, predictors = patsy.dmatrices('D2 ~ D1', df)
如果检查“结果”和“预测变量”的类型,你会发现它们是DesignMatrix类型的自定义 patsy 对象。
如果你将它们打印出来,你会看到它们重置了 Pandas Series或DataFrames。
你可以将它们视为自定义的类数据帧对象,以便将其组织成用于建模的矩阵。
# 现在使用 statsmodels 初始化 OLS 线性模型
# 此步骤初始化模型,并提供数据(但实际上不计算模型)
mod = sm.OLS(outcome, predictors)
请注意,statsmodels,就像我们稍后会遇到的 scikit-learn 一样,使用面向对象的方法。
在这种方法中,你初始化将数据和方法存储在一起的复杂对象,为你提供有组织的方式来存储和检查数据和参数,拟合模型,然后甚至使用它们进行预测等等。
# 检查我们刚刚创建的模型对象的类型。
# 你还可以使用 tab 补全,来探索此对象的可用内容
type(mod)
# statsmodels.regression.linear_model.OLS
# 最后,拟合模型
res = mod.fit()
# 检查结果
print(res.summary())
'''
==============================================================================
Dep. Variable: D2 R-squared: 0.558
Model: OLS Adj. R-squared: 0.558
Method: Least Squares F-statistic: 1261.
Date: Tue, 06 Mar 2018 Prob (F-statistic): 3.32e-179
Time: 00:18:34 Log-Likelihood: -993.04
No. Observations: 1000 AIC: 1990.
Df Residuals: 998 BIC: 2000.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0011 0.021 0.054 0.957 -0.039 0.042
D1 0.7546 0.021 35.506 0.000 0.713 0.796
==============================================================================
Omnibus: 1.644 Durbin-Watson: 1.970
Prob(Omnibus): 0.440 Jarque-Bera (JB): 1.508
Skew: -0.068 Prob(JB): 0.470
Kurtosis: 3.133 Cond. No. 1.05
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
'''
解释输出
Statsmodels 为我们提供了大量信息!
最上面的部分主要是元数据:它包括模型类型,运行它的时间和日期等内容。
它还包括 R 方,它是模型能够捕获的方差量的总体汇总。这个值在 0-1 之间,约为 0.5 ,我们在这里看到,是一个非常高的值,表明模型拟合良好。
中间一列是实际的模型结果。
每行反映一个参数,并给出它的值(coef),误差(std err),统计检验结果,关于该参数是否是输出变量的显着预测值(t,其中相关的 p 值为'P > | t |),以及参数值的置信区间([0.025 - 0.975]`)。
最后一个模型包括对数据运行的一些其他测试,可以帮助你检查输入数据的某些描述符,以及它们是否满足这种模型拟合的必要条件。
检查我们的模型
就模型本身而言,最有用的组件位于第二行,其中摘要给出了参数值,以及我们的预测变量的 p 值,在这种情况下是Intercept和D2。
从上面的结果中,我们可以获取参数的值,并获得以下模型:
D2 = -0.0284 + 0.7246 * D1
但是,我们还应该记住报告的统计测试,参数值是否显着(显着不同于零)的测试。使用 0.05 的 alpha 值,在这种情况下,D2参数值是显着的,但Intercept值不是。由于Intercept的参数值与零没有显着差异,我们可以决定不将它包含在我们的最终模型中。
因此,我们完成了模型:
D2 = 0.7246 * D1
有了这个模型,a1的值很可能为 0.7246,非常接近数据点的相关值,我们将其设置为 0.75!
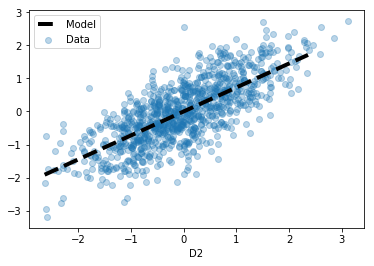
## 绘制模型的拟合直线
# 绘制原始数据(像之前一样)
plt.scatter(df['D1'], df['D2'], alpha=0.3, label='Data');
# 生成和绘制模型的拟合直线
xs = np.arange(df['D1'].min(), df['D1'].max())
ys = 0.7246 * xs
plt.plot(xs, ys, '--k', linewidth=4, label='Model')
plt.xlabel('D1')
plt.xlabel('D2')
plt.legend();
使用多个预测值
上面的模型只使用了一个预测值,拟合了一条简单的直线,因此实际上模仿了我们用于拟合直线的先前方法。
我们还可以拟合多个预测变量,这就是 patsy 和 statsmodel 的强大功能,因为这些函数你和更复杂的模型,包括我们想要的许多参数,也处理相关特征的某些方面,等等。
在这里,我们将向数据帧添加一个新变量,并使用两个预测变量拟合 OLS 模型。
# 向 df 添加数据的新列
df['D3'] = pd.Series(np.random.randn(1000), index=df.index)
df.head()
| D1 | D2 | D3 | |
|---|---|---|---|
| 0 | 0.305994 | 0.521119 | 0.019043 |
| 1 | 0.262456 | 0.562350 | -0.631288 |
| 2 | -0.289970 | 0.608496 | 0.794971 |
| 3 | 0.025279 | 0.523315 | 0.447560 |
| 4 | -0.561126 | -1.320507 | -1.560199 |
# 从 D2 和 D3 预测 D1
outcome, predictors = patsy.dmatrices('D1 ~ D2 + D3', df)
mod = sm.OLS(outcome, predictors)
res = mod.fit()
# 检查模型拟合摘要
print(res.summary())
'''
==============================================================================
Dep. Variable: D1 R-squared: 0.558
Model: OLS Adj. R-squared: 0.557
Method: Least Squares F-statistic: 630.1
Date: Tue, 06 Mar 2018 Prob (F-statistic): 1.25e-177
Time: 00:18:34 Log-Likelihood: -982.91
No. Observations: 1000 AIC: 1972.
Df Residuals: 997 BIC: 1987.
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -0.0177 0.020 -0.866 0.387 -0.058 0.022
D2 0.7395 0.021 35.479 0.000 0.699 0.780
D3 -0.0121 0.021 -0.587 0.557 -0.052 0.028
==============================================================================
Omnibus: 0.273 Durbin-Watson: 1.993
Prob(Omnibus): 0.872 Jarque-Bera (JB): 0.357
Skew: -0.019 Prob(JB): 0.836
Kurtosis: 2.916 Cond. No. 1.04
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
'''
请注意,如上所述,statsmodels 是一种功能强大的通用 OLS 模型方法。
你可以进一步研究如何包含其他功能,例如输入变量之间的交互,等等。
sklearn 线性回归
Scikit-learn 也具有线性回归模型的实现。
在这里,我们将使用 sklearn 而不是 statsmodels,快速演示运行与上述相同的线性 OLS 模型。
sklearn 中的线性回归。
# sklearn 的线性模型
from sklearn import linear_model
# 转换数据的形状,便于 sklearn 使用
d1 = np.reshape(df.D1.values, [len(df.D1), 1])
d2 = np.reshape(df.D2.values, [len(df.D2), 1])
d3 = np.reshape(df.D3.values, [len(df.D3), 1])
# 初始化线性回归模型
reg = linear_model.LinearRegression()
# 拟合线性回归模型
reg.fit(d2, d1) #d1 = a0 + a1*d2
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# 检查这个结果
# 如果将这些与我们上面使用的 statsmodel 进行比较,它们确实是相同的
print(reg.intercept_[0])
print(reg.coef_[0][0])
'''
-0.0179497213127
0.739686393719
'''
(在 sklearn 中)使用多个预测变量
# 初始化并拟合线性模型
# d1 = a1*d2 + a2*d3 + a0
reg = linear_model.LinearRegression()
reg.fit(np.hstack([d2, d3]), d1)
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
np.hstack([d2, d3]).shape
# (1000, 2)
# 检查这个结果
# 如果将这些与我们上面使用的 statsmodel 进行比较,它们确实是相同的
print('Intercept: \t', reg.intercept_[0])
print('Theta D2 :\t', reg.coef_[0][0])
print('Theta D3 :\t', reg.coef_[0][1])
'''
Intercept: -0.0177498825239
Theta D2 : 0.739473377018
Theta D3 : -0.0120672090985
'''