Dynamic Recurrent Neural Network.
TensorFlow implementation of a Recurrent Neural Network (LSTM) that performs dynamic computation over sequences with variable length. This example is using a toy dataset to classify linear sequences. The generated sequences have variable length.
- Author: Aymeric Damien
- Project: https://github.com/aymericdamien/TensorFlow-Examples/
RNN Overview
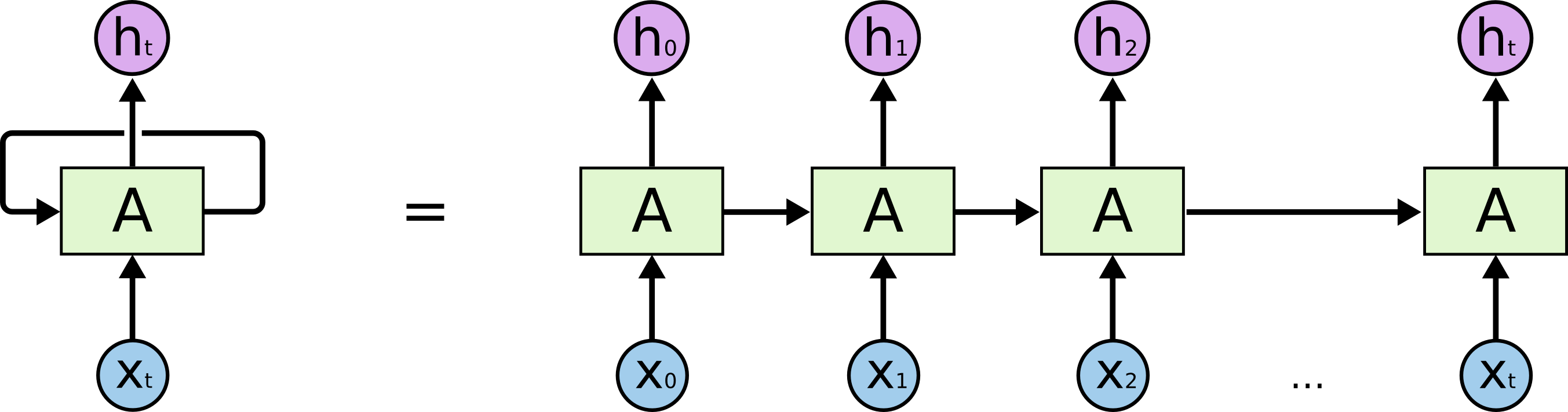
References:
- Long Short Term Memory, Sepp Hochreiter & Jurgen Schmidhuber, Neural Computation 9(8): 1735-1780, 1997.
from __future__ import print_function
import tensorflow as tf
import random
# ====================
# TOY DATA GENERATOR
# ====================
class ToySequenceData(object):
""" Generate sequence of data with dynamic length.
This class generate samples for training:
- Class 0: linear sequences (i.e. [0, 1, 2, 3,...])
- Class 1: random sequences (i.e. [1, 3, 10, 7,...])
NOTICE:
We have to pad each sequence to reach 'max_seq_len' for TensorFlow
consistency (we cannot feed a numpy array with inconsistent
dimensions). The dynamic calculation will then be perform thanks to
'seqlen' attribute that records every actual sequence length.
"""
def __init__(self, n_samples=1000, max_seq_len=20, min_seq_len=3,
max_value=1000):
self.data = []
self.labels = []
self.seqlen = []
for i in range(n_samples):
# Random sequence length
len = random.randint(min_seq_len, max_seq_len)
# Monitor sequence length for TensorFlow dynamic calculation
self.seqlen.append(len)
# Add a random or linear int sequence (50% prob)
if random.random() < .5:
# Generate a linear sequence
rand_start = random.randint(0, max_value - len)
s = [[float(i)/max_value] for i in
range(rand_start, rand_start + len)]
# Pad sequence for dimension consistency
s += [[0.] for i in range(max_seq_len - len)]
self.data.append(s)
self.labels.append([1., 0.])
else:
# Generate a random sequence
s = [[float(random.randint(0, max_value))/max_value]
for i in range(len)]
# Pad sequence for dimension consistency
s += [[0.] for i in range(max_seq_len - len)]
self.data.append(s)
self.labels.append([0., 1.])
self.batch_id = 0
def next(self, batch_size):
""" Return a batch of data. When dataset end is reached, start over.
"""
if self.batch_id == len(self.data):
self.batch_id = 0
batch_data = (self.data[self.batch_id:min(self.batch_id +
batch_size, len(self.data))])
batch_labels = (self.labels[self.batch_id:min(self.batch_id +
batch_size, len(self.data))])
batch_seqlen = (self.seqlen[self.batch_id:min(self.batch_id +
batch_size, len(self.data))])
self.batch_id = min(self.batch_id + batch_size, len(self.data))
return batch_data, batch_labels, batch_seqlen
# ==========
# MODEL
# ==========
# Parameters
learning_rate = 0.01
training_steps = 10000
batch_size = 128
display_step = 200
# Network Parameters
seq_max_len = 20 # Sequence max length
n_hidden = 64 # hidden layer num of features
n_classes = 2 # linear sequence or not
trainset = ToySequenceData(n_samples=1000, max_seq_len=seq_max_len)
testset = ToySequenceData(n_samples=500, max_seq_len=seq_max_len)
# tf Graph input
x = tf.placeholder("float", [None, seq_max_len, 1])
y = tf.placeholder("float", [None, n_classes])
# A placeholder for indicating each sequence length
seqlen = tf.placeholder(tf.int32, [None])
# Define weights
weights = {
'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([n_classes]))
}
def dynamicRNN(x, seqlen, weights, biases):
# Prepare data shape to match `rnn` function requirements
# Current data input shape: (batch_size, n_steps, n_input)
# Required shape: 'n_steps' tensors list of shape (batch_size, n_input)
# Unstack to get a list of 'n_steps' tensors of shape (batch_size, n_input)
x = tf.unstack(x, seq_max_len, 1)
# Define a lstm cell with tensorflow
lstm_cell = tf.contrib.rnn.BasicLSTMCell(n_hidden)
# Get lstm cell output, providing 'sequence_length' will perform dynamic
# calculation.
outputs, states = tf.contrib.rnn.static_rnn(lstm_cell, x, dtype=tf.float32,
sequence_length=seqlen)
# When performing dynamic calculation, we must retrieve the last
# dynamically computed output, i.e., if a sequence length is 10, we need
# to retrieve the 10th output.
# However TensorFlow doesn't support advanced indexing yet, so we build
# a custom op that for each sample in batch size, get its length and
# get the corresponding relevant output.
# 'outputs' is a list of output at every timestep, we pack them in a Tensor
# and change back dimension to [batch_size, n_step, n_input]
outputs = tf.stack(outputs)
outputs = tf.transpose(outputs, [1, 0, 2])
# Hack to build the indexing and retrieve the right output.
batch_size = tf.shape(outputs)[0]
# Start indices for each sample
index = tf.range(0, batch_size) * seq_max_len + (seqlen - 1)
# Indexing
outputs = tf.gather(tf.reshape(outputs, [-1, n_hidden]), index)
# Linear activation, using outputs computed above
return tf.matmul(outputs, weights['out']) + biases['out']
pred = dynamicRNN(x, seqlen, weights, biases)
# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()
/Users/aymeric.damien/anaconda2/lib/python2.7/site-packages/tensorflow/python/ops/gradients_impl.py:93: UserWarning: Converting sparse IndexedSlices to a dense Tensor of unknown shape. This may consume a large amount of memory.
"Converting sparse IndexedSlices to a dense Tensor of unknown shape. "
# Start training
with tf.Session() as sess:
# Run the initializer
sess.run(init)
for step in range(1, training_steps+1):
batch_x, batch_y, batch_seqlen = trainset.next(batch_size)
# Run optimization op (backprop)
sess.run(optimizer, feed_dict={x: batch_x, y: batch_y,
seqlen: batch_seqlen})
if step % display_step == 0 or step == 1:
# Calculate batch accuracy & loss
acc, loss = sess.run([accuracy, cost], feed_dict={x: batch_x, y: batch_y,
seqlen: batch_seqlen})
print("Step " + str(step) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
print("Optimization Finished!")
# Calculate accuracy
test_data = testset.data
test_label = testset.labels
test_seqlen = testset.seqlen
print("Testing Accuracy:", \
sess.run(accuracy, feed_dict={x: test_data, y: test_label,
seqlen: test_seqlen}))
Step 1, Minibatch Loss= 0.864517, Training Accuracy= 0.42188
Step 200, Minibatch Loss= 0.686012, Training Accuracy= 0.43269
Step 400, Minibatch Loss= 0.682970, Training Accuracy= 0.48077
Step 600, Minibatch Loss= 0.679640, Training Accuracy= 0.50962
Step 800, Minibatch Loss= 0.675208, Training Accuracy= 0.53846
Step 1000, Minibatch Loss= 0.668636, Training Accuracy= 0.56731
Step 1200, Minibatch Loss= 0.657525, Training Accuracy= 0.62500
Step 1400, Minibatch Loss= 0.635423, Training Accuracy= 0.67308
Step 1600, Minibatch Loss= 0.580433, Training Accuracy= 0.75962
Step 1800, Minibatch Loss= 0.475599, Training Accuracy= 0.81731
Step 2000, Minibatch Loss= 0.434865, Training Accuracy= 0.83654
Step 2200, Minibatch Loss= 0.423690, Training Accuracy= 0.85577
Step 2400, Minibatch Loss= 0.417472, Training Accuracy= 0.85577
Step 2600, Minibatch Loss= 0.412906, Training Accuracy= 0.85577
Step 2800, Minibatch Loss= 0.409193, Training Accuracy= 0.85577
Step 3000, Minibatch Loss= 0.406035, Training Accuracy= 0.86538
Step 3200, Minibatch Loss= 0.403287, Training Accuracy= 0.87500
Step 3400, Minibatch Loss= 0.400862, Training Accuracy= 0.87500
Step 3600, Minibatch Loss= 0.398704, Training Accuracy= 0.86538
Step 3800, Minibatch Loss= 0.396768, Training Accuracy= 0.86538
Step 4000, Minibatch Loss= 0.395017, Training Accuracy= 0.86538
Step 4200, Minibatch Loss= 0.393422, Training Accuracy= 0.86538
Step 4400, Minibatch Loss= 0.391957, Training Accuracy= 0.85577
Step 4600, Minibatch Loss= 0.390600, Training Accuracy= 0.85577
Step 4800, Minibatch Loss= 0.389334, Training Accuracy= 0.86538
Step 5000, Minibatch Loss= 0.388143, Training Accuracy= 0.86538
Step 5200, Minibatch Loss= 0.387015, Training Accuracy= 0.86538
Step 5400, Minibatch Loss= 0.385940, Training Accuracy= 0.86538
Step 5600, Minibatch Loss= 0.384907, Training Accuracy= 0.86538
Step 5800, Minibatch Loss= 0.383904, Training Accuracy= 0.85577
Step 6000, Minibatch Loss= 0.382921, Training Accuracy= 0.86538
Step 6200, Minibatch Loss= 0.381941, Training Accuracy= 0.86538
Step 6400, Minibatch Loss= 0.380947, Training Accuracy= 0.86538
Step 6600, Minibatch Loss= 0.379912, Training Accuracy= 0.86538
Step 6800, Minibatch Loss= 0.378796, Training Accuracy= 0.86538
Step 7000, Minibatch Loss= 0.377540, Training Accuracy= 0.86538
Step 7200, Minibatch Loss= 0.376041, Training Accuracy= 0.86538
Step 7400, Minibatch Loss= 0.374130, Training Accuracy= 0.85577
Step 7600, Minibatch Loss= 0.371514, Training Accuracy= 0.85577
Step 7800, Minibatch Loss= 0.367723, Training Accuracy= 0.85577
Step 8000, Minibatch Loss= 0.362049, Training Accuracy= 0.85577
Step 8200, Minibatch Loss= 0.353558, Training Accuracy= 0.85577
Step 8400, Minibatch Loss= 0.341072, Training Accuracy= 0.86538
Step 8600, Minibatch Loss= 0.323062, Training Accuracy= 0.87500
Step 8800, Minibatch Loss= 0.299278, Training Accuracy= 0.89423
Step 9000, Minibatch Loss= 0.273857, Training Accuracy= 0.90385
Step 9200, Minibatch Loss= 0.248392, Training Accuracy= 0.91346
Step 9400, Minibatch Loss= 0.221348, Training Accuracy= 0.92308
Step 9600, Minibatch Loss= 0.191947, Training Accuracy= 0.92308
Step 9800, Minibatch Loss= 0.159308, Training Accuracy= 0.93269
Step 10000, Minibatch Loss= 0.136938, Training Accuracy= 0.96154
Optimization Finished!
Testing Accuracy: 0.952