Powered by GitBook

Variational Auto-Encoder Example

Build a variational auto-encoder (VAE) to generate digit images from a noise distribution with TensorFlow.

Author: Aymeric Damien
Project: https://github.com/aymericdamien/TensorFlow-Examples/

VAE Overview

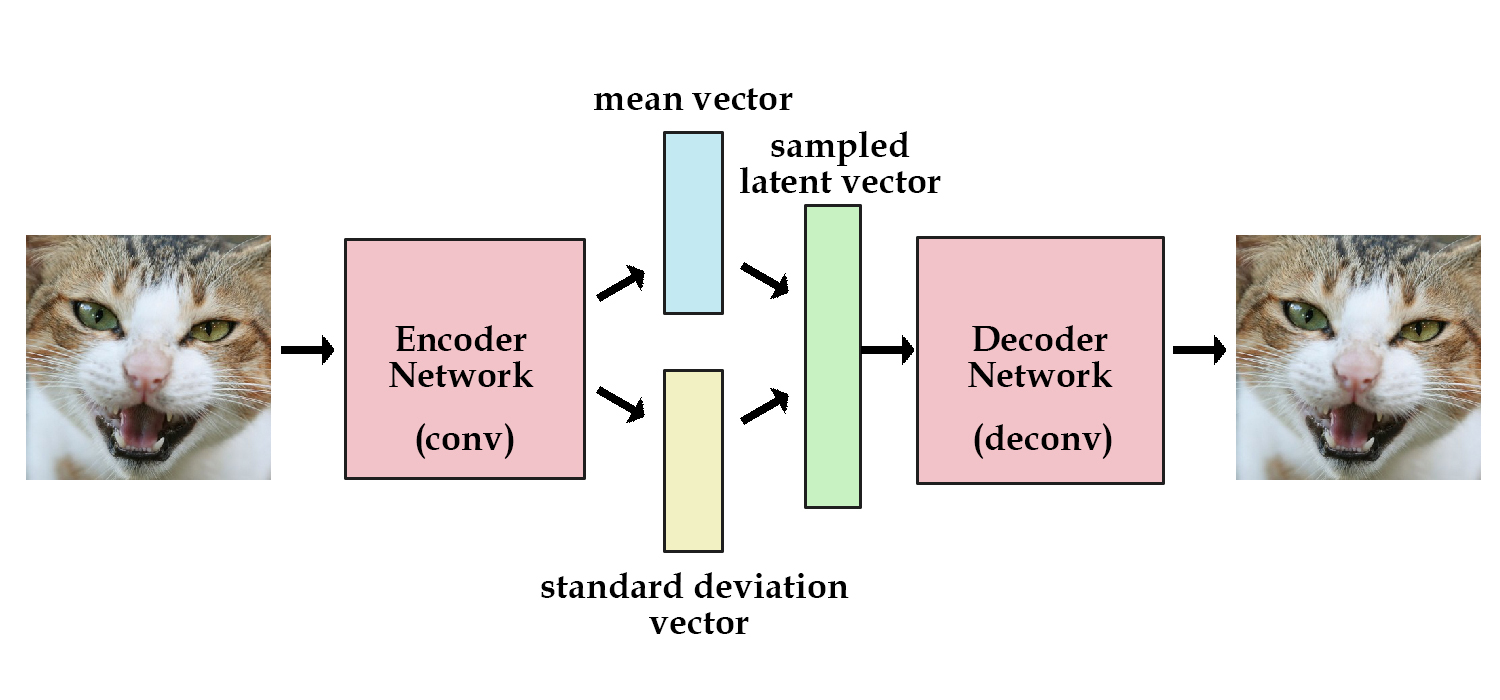
References:

Auto-Encoding Variational Bayes The International Conference on Learning Representations (ICLR), Banff, 2014. D.P. Kingma, M. Welling
Understanding the difficulty of training deep feedforward neural networks. X Glorot, Y Bengio. Aistats 9, 249-256

Other tutorials:

Variational Auto Encoder Explained. Kevin Frans.

MNIST Dataset Overview

This example is using MNIST handwritten digits. The dataset contains 60,000 examples for training and 10,000 examples for testing. The digits have been size-normalized and centered in a fixed-size image (28x28 pixels) with values from 0 to 1. For simplicity, each image has been flattened and converted to a 1-D numpy array of 784 features (28*28).

More info: http://yann.lecun.com/exdb/mnist/

from __future__ import division, print_function, absolute_import

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import tensorflow as tf

# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

Successfully downloaded train-images-idx3-ubyte.gz 9912422 bytes.
Extracting /tmp/data/train-images-idx3-ubyte.gz
Successfully downloaded train-labels-idx1-ubyte.gz 28881 bytes.
Extracting /tmp/data/train-labels-idx1-ubyte.gz
Successfully downloaded t10k-images-idx3-ubyte.gz 1648877 bytes.
Extracting /tmp/data/t10k-images-idx3-ubyte.gz
Successfully downloaded t10k-labels-idx1-ubyte.gz 4542 bytes.
Extracting /tmp/data/t10k-labels-idx1-ubyte.gz

# Parameters
learning_rate = 0.001
num_steps = 30000
batch_size = 64

# Network Parameters
image_dim = 784 # MNIST images are 28x28 pixels
hidden_dim = 512
latent_dim = 2

# A custom initialization (see Xavier Glorot init)
def glorot_init(shape):
    return tf.random_normal(shape=shape, stddev=1. / tf.sqrt(shape[0] / 2.))

# Variables
weights = {
    'encoder_h1': tf.Variable(glorot_init([image_dim, hidden_dim])),
    'z_mean': tf.Variable(glorot_init([hidden_dim, latent_dim])),
    'z_std': tf.Variable(glorot_init([hidden_dim, latent_dim])),
    'decoder_h1': tf.Variable(glorot_init([latent_dim, hidden_dim])),
    'decoder_out': tf.Variable(glorot_init([hidden_dim, image_dim]))
}
biases = {
    'encoder_b1': tf.Variable(glorot_init([hidden_dim])),
    'z_mean': tf.Variable(glorot_init([latent_dim])),
    'z_std': tf.Variable(glorot_init([latent_dim])),
    'decoder_b1': tf.Variable(glorot_init([hidden_dim])),
    'decoder_out': tf.Variable(glorot_init([image_dim]))
}

# Building the encoder
input_image = tf.placeholder(tf.float32, shape=[None, image_dim])
encoder = tf.matmul(input_image, weights['encoder_h1']) + biases['encoder_b1']
encoder = tf.nn.tanh(encoder)
z_mean = tf.matmul(encoder, weights['z_mean']) + biases['z_mean']
z_std = tf.matmul(encoder, weights['z_std']) + biases['z_std']

# Sampler: Normal (gaussian) random distribution
eps = tf.random_normal(tf.shape(z_std), dtype=tf.float32, mean=0., stddev=1.0,
                       name='epsilon')
z = z_mean + tf.exp(z_std / 2) * eps

# Building the decoder (with scope to re-use these layers later)
decoder = tf.matmul(z, weights['decoder_h1']) + biases['decoder_b1']
decoder = tf.nn.tanh(decoder)
decoder = tf.matmul(decoder, weights['decoder_out']) + biases['decoder_out']
decoder = tf.nn.sigmoid(decoder)

# Define VAE Loss
def vae_loss(x_reconstructed, x_true):
    # Reconstruction loss
    encode_decode_loss = x_true * tf.log(1e-10 + x_reconstructed) \
                         + (1 - x_true) * tf.log(1e-10 + 1 - x_reconstructed)
    encode_decode_loss = -tf.reduce_sum(encode_decode_loss, 1)
    # KL Divergence loss
    kl_div_loss = 1 + z_std - tf.square(z_mean) - tf.exp(z_std)
    kl_div_loss = -0.5 * tf.reduce_sum(kl_div_loss, 1)
    return tf.reduce_mean(encode_decode_loss + kl_div_loss)

loss_op = vae_loss(decoder, input_image)
optimizer = tf.train.RMSPropOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op)

# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()

# Start Training
# Start a new TF session
sess = tf.Session()

# Run the initializer
sess.run(init)

# Training
for i in range(1, num_steps+1):
    # Prepare Data
    # Get the next batch of MNIST data (only images are needed, not labels)
    batch_x, _ = mnist.train.next_batch(batch_size)

    # Train
    feed_dict = {input_image: batch_x}
    _, l = sess.run([train_op, loss_op], feed_dict=feed_dict)
    if i % 1000 == 0 or i == 1:
        print('Step %i, Loss: %f' % (i, l))

Step 1, Loss: 645.076538
Step 1000, Loss: 173.018188
Step 2000, Loss: 165.299225
Step 3000, Loss: 172.933685
Step 4000, Loss: 161.475052
Step 5000, Loss: 179.529831
Step 6000, Loss: 166.430023
Step 7000, Loss: 167.152176
Step 8000, Loss: 159.920242
Step 9000, Loss: 160.172363
Step 10000, Loss: 150.077652
Step 11000, Loss: 162.774567
Step 12000, Loss: 156.187820
Step 13000, Loss: 148.331573
Step 14000, Loss: 153.757202
Step 15000, Loss: 158.050598
Step 16000, Loss: 163.068939
Step 17000, Loss: 152.765152
Step 18000, Loss: 151.136353
Step 19000, Loss: 157.889664
Step 20000, Loss: 149.112473
Step 21000, Loss: 151.694885
Step 22000, Loss: 153.153229
Step 23000, Loss: 152.662323
Step 24000, Loss: 150.556198
Step 25000, Loss: 142.779984
Step 26000, Loss: 148.985382
Step 27000, Loss: 150.923401
Step 28000, Loss: 161.761551
Step 29000, Loss: 144.045578
Step 30000, Loss: 151.272964

# Testing
# Generator takes noise as input
noise_input = tf.placeholder(tf.float32, shape=[None, latent_dim])
# Rebuild the decoder to create image from noise
decoder = tf.matmul(noise_input, weights['decoder_h1']) + biases['decoder_b1']
decoder = tf.nn.tanh(decoder)
decoder = tf.matmul(decoder, weights['decoder_out']) + biases['decoder_out']
decoder = tf.nn.sigmoid(decoder)

# Building a manifold of generated digits
n = 20
x_axis = np.linspace(-3, 3, n)
y_axis = np.linspace(-3, 3, n)

canvas = np.empty((28 * n, 28 * n))
for i, yi in enumerate(x_axis):
    for j, xi in enumerate(y_axis):
        z_mu = np.array([[xi, yi]] * batch_size)
        x_mean = sess.run(decoder, feed_dict={noise_input: z_mu})
        canvas[(n - i - 1) * 28:(n - i) * 28, j * 28:(j + 1) * 28] = \
        x_mean[0].reshape(28, 28)

plt.figure(figsize=(8, 10))
Xi, Yi = np.meshgrid(x_axis, y_axis)
plt.imshow(canvas, origin="upper", cmap="gray")
plt.show()

results matching ""

No results matching ""