二十一、统计学
作者:Chris Albon
译者:飞龙
贝塞尔校正
贝塞尔的校正是我们在样本方差和样本标准差的计算中使用 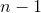 而不是
而不是 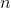 的原因。
的原因。
样本方差:
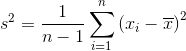
当我们计算样本方差时,我们试图估计总体方差,这是一个未知值。 为了进行这种估计,我们从样本与总体均值的平方差的平均值,来估计未知的总体方差。 这种估计技术的负面影响是,因为我们正在采样,我们更有可能观察到差较小的观测,因为它们更常见(例如它们是分布的中心)。 按照定义我们将低估总体方差。
弗里德里希贝塞尔发现,通过将有偏差(未校正)的样本方差 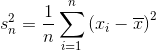 乘以
乘以 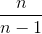 ,我们将能够减少这种偏差,从而能够准确估计总体方差和标准差。 乘法的最终结果是无偏样本方差。
,我们将能够减少这种偏差,从而能够准确估计总体方差和标准差。 乘法的最终结果是无偏样本方差。
演示中心极限定律
# 导入包
import pandas as pd
import numpy as np
# 将 matplotlib 设为内联
%matplotlib inline
# 创建空的数据帧
population = pd.DataFrame()
# 创建一列,它是来自均匀分布的 10000 个随机数
population['numbers'] = np.random.uniform(0,10000,size=10000)
# 绘制得分数据的直方图
# 这确认了数据不是正态分布的
population['numbers'].hist(bins=100)
# <matplotlib.axes._subplots.AxesSubplot at 0x112c72710>

# 查看数值的均值
population['numbers'].mean()
# 4983.824612472138
# 创建列表
sampled_means = []
# 执行 1000 次
for i in range(0,1000):
# 从总体中随机抽取 100 行
# 计算它们的均值,附加到 sampled_means
sampled_means.append(population.sample(n=100).mean().values[0])
# 绘制 sampled_means 的直方图
# 它很明显是正态分布的,中心约为 5000
pd.Series(sampled_means).hist(bins=100)
# <matplotlib.axes._subplots.AxesSubplot at 0x11516e668>

这是关键的图表,记住总体分布是均匀的,然而,这个分布接近正态。 这是中心极限理论的关键点,也是我们可以假设样本均值是无偏的原因。
# 查看 sampled_means 的均值
pd.Series(sampled_means).mean()
# 4981.465310909289
# 将样本均值的均值减去真实的总体均值
error = population['numbers'].mean() - pd.Series(sampled_means).mean()
# 打印
print('The Mean Sample Mean is only %f different the True Population mean!' % error)
# The Mean Sample Mean is only 2.359302 different the True Population mean!
皮尔逊相关系数
基于 cbare 的这个 StackOverflow 答案。
import statistics as stats
x = [1,2,3,4,5,6,7,8,9]
y = [2,1,2,4.5,7,6.5,6,9,9.5]
有许多等价的表达方式来计算皮尔逊相关系数(也称为皮尔逊的 r)。这是一个。
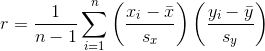
其中 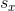 和
和 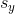 是
是 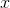 和
和 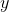 的标准差,
的标准差,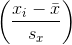 是
是 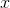 和
和 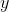 的标准得分。
的标准得分。
# 创建函数
def pearson(x,y):
# 创建 n,数据中的观测数量
n = len(x)
# 创建列表来储存标准得分
standard_score_x = []
standard_score_y = []
# 计算 x 的均值
mean_x = stats.mean(x)
# 计算 x 的标准差
standard_deviation_x = stats.stdev(x)
# 计算 y 的均值
mean_y = stats.mean(y)
# 计算 y 的标准差
standard_deviation_y = stats.stdev(y)
# 对于 x 中的每个观测
for observation in x:
# 计算 x 的标准得分
standard_score_x.append((observation - mean_x)/standard_deviation_x)
# 对于 y 中的每个观测
for observation in y:
# 计算 y 的标准得分
standard_score_y.append((observation - mean_y)/standard_deviation_y)
# 将标准得分加在一起,求和,然后除以 n-1,返回该值
return (sum([i*j for i,j in zip(standard_score_x, standard_score_y)]))/(n-1)
# 展示皮尔逊相关系数
pearson(x,y)
# 0.9412443251336238
概率质量函数(PMF)
# 加载库
import matplotlib.pyplot as plt
# 创建一些随机整数
data = [3,2,3,4,2,3,5,2,2,3,3,5,2,2,5,6,2,2,2,3,6,6,2,4,3,2,3]
# 创建字典来储存计数
count = {}
# 对于数据中的每个值
for observation in data:
# 键为观测,值递增
count[observation] = count.get(observation, 0) + 1
# 计算观测数量 observations
n = len(data)
# 创建字典
probability_mass_function = {}
# 对于每个唯一值
for unique_value, count in count.items():
# 将计数归一化,通过除以数据量,添加到 PMC 字典
probability_mass_function[unique_value] = count / n
# 绘制概率质量函数
plt.bar(list(probability_mass_function.keys()), probability_mass_function.values(), color='g')
plt.show()

Spearman 排名相关度
import numpy as np
import pandas as pd
import scipy.stats
# 创建两列随机变量
x = [1,2,3,4,5,6,7,8,9]
y = [2,1,2,4.5,7,6.5,6,9,9.5]
Spearman 的排名相关度,是变量的排名版本的皮尔逊相关系数。
# 创建接受 x 和 y 的函数
def spearmans_rank_correlation(xs, ys):
# 计算 x 的排名
#(也就是排序后元素的位置)
xranks = pd.Series(xs).rank()
# 计算 y 的排名
yranks = pd.Series(ys).rank()
# 在数据的排名版本上,计算皮尔逊相关系数
return scipy.stats.pearsonr(xranks, yranks)
# 运行函数
spearmans_rank_correlation(x, y)[0]
# 0.90377360145618091
# 仅仅检查我们的结果,使用 Scipy 的 Spearman
scipy.stats.spearmanr(x, y)[0]
# 0.90377360145618102
T 检验
from scipy import stats
import numpy as np
# 创建 20 个观测的列表,从均值为 1,
# 标准差为 1.5 的正态分布中随机抽取
x = np.random.normal(1, 1.5, 20)
# 创建 20 个观测的列表,从均值为 0,
# 标准差为 1.5 的正态分布中随机抽取
y = np.random.normal(0, 1.5, 20)
单样本双边 T 检验
想象一下单样本 T 检验,并绘制一个“正态形状的”山丘,以1为中心,并以1.5为标准差而“展开”,然后在0处放置一个标志并查看标志在山丘上的位置。它靠近顶部吗? 或者远离山丘? 如果标志靠近山丘的底部或更远,则 t 检验的 p 值将低于0.05。
# 运行 T 检验来检验 x 的均值和 0 相比,是否有统计学显著的差异
pvalue = stats.ttest_1samp(x, 0)[1]
# 查看 p 值
pvalue
# 0.00010976647757800537
双样本非配对等方差双边 T 检验
想象一下单样本 T 检验,并根据标准差绘制两个(正态形状的)山丘,以它们的均值为中心,并根据他们的标准差绘制它们的“平坦度”(个体延展度)。 T 检验考察了两座山丘重叠的程度。 它们基本上是彼此覆盖的吗? 山丘的底部几乎没有碰到吗? 如果山丘的尾部刚刚重叠或根本不重叠,则 t 检验的 p 值将低于 0.05。
stats.ttest_ind(x, y)[1]
# 0.00035082056802728071
stats.ttest_ind(x, y, equal_var=False)[1]
# 0.00035089238660076095
双样本配对双边 T 检验
当我们采集重复样本,并且想要考虑我们正在测试的两个分布是成对的这一事实时,使用配对 T 检验。
stats.ttest_rel(x, y)[1]
# 0.00034222792790150386
方差和标准差
# 导入包
import math
# 创建值的列表
data = [3,2,3,4,2,3,5,2,2,33,3,5,2,2,5,6,62,2,2,3,6,6,2,23,3,2,3]
方差是衡量数据分布延展度的指标。 方差越大,数据点越“分散”。 方差,通常表示为 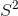 ,计算方式如下:
,计算方式如下:
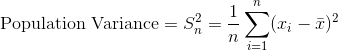

其中 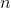 是观测数,
是观测数,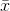 是观察值的平均值,
是观察值的平均值,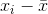 是单个观察值减去数据均值。 请注意,如果我们根据来自该总体的样本估计总体的方差,我们应该使用第二个等式,将
是单个观察值减去数据均值。 请注意,如果我们根据来自该总体的样本估计总体的方差,我们应该使用第二个等式,将 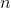 替换为
替换为 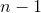 。
。
# 计算 n
n = len(data)
# 计算均值
mean = sum(data)/len(data)
# 从均值创建所有观测的差
all_deviations_from_mean_squared = []
# 对于数据中的每个观测
for observation in data:
# 计算到均值的差
deviation_from_mean = (observation - mean)
# 计算平方
deviation_from_mean_squared = deviation_from_mean**2
# 将结果添加到列表
all_deviations_from_mean_squared.append(deviation_from_mean_squared)
# 对于列表中所有平方差求和
sum_of_deviations_from_mean_squared = sum(all_deviations_from_mean_squared)
# 除以 n
population_variance = sum_of_deviations_from_mean_squared/n
# 展示方差
population_variance
# 160.78463648834017
标准差就是方差的平方根。
# 计算总体方差的平方根
population_standard_deviation = math.sqrt(population_variance)
# 打印总体标准差
population_standard_deviation
# 12.68008818929664