八、特征选择
作者:Chris Albon
译者:飞龙
用于特征选取的 ANOVA F 值
如果特征是类别的,计算每个特征与目标向量之间的卡方(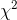 )统计量。 但是,如果特征是定量的,则计算每个特征与目标向量之间的 ANOVA F 值。
)统计量。 但是,如果特征是定量的,则计算每个特征与目标向量之间的 ANOVA F 值。
F 值得分检查当我们按照目标向量对数字特征进行分组时,每个组的均值是否显着不同。
# 加载库
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_classif
# 加载鸢尾花数据
iris = load_iris()
# 创建特征和标签
X = iris.data
y = iris.target
# 创建 SelectKBest 对象来选择两个带有最佳 ANOVA F 值的特征
fvalue_selector = SelectKBest(f_classif, k=2)
# 对 SelectKBest 对象应用特征和标签
X_kbest = fvalue_selector.fit_transform(X, y)
# 展示结果
print('Original number of features:', X.shape[1])
print('Reduced number of features:', X_kbest.shape[1])
'''
Original number of features: 4
Reduced number of features: 2
'''
用于特征选择的卡方

# 加载库
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
# 加载鸢尾花数据
iris = load_iris()
# 创建特征和目标
X = iris.data
y = iris.target
# 通过将数据转换为整数,转换为类别数据
X = X.astype(int)
# 选择两个卡方统计量最高的特征
chi2_selector = SelectKBest(chi2, k=2)
X_kbest = chi2_selector.fit_transform(X, y)
# 展示结果
print('Original number of features:', X.shape[1])
print('Reduced number of features:', X_kbest.shape[1])
'''
Original number of features: 4
Reduced number of features: 2
'''
丢弃高度相关的特征
# 加载库
import pandas as pd
import numpy as np
# 创建特征矩阵,具有两个高度相关特征
X = np.array([[1, 1, 1],
[2, 2, 0],
[3, 3, 1],
[4, 4, 0],
[5, 5, 1],
[6, 6, 0],
[7, 7, 1],
[8, 7, 0],
[9, 7, 1]])
# 将特征矩阵转换为 DataFrame
df = pd.DataFrame(X)
# 查看数据帧
df
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 2 | 2 | 0 |
| 2 | 3 | 3 | 1 |
| 3 | 4 | 4 | 0 |
| 4 | 5 | 5 | 1 |
| 5 | 6 | 6 | 0 |
| 6 | 7 | 7 | 1 |
| 7 | 8 | 7 | 0 |
| 8 | 9 | 7 | 1 |
# 创建相关度矩阵
corr_matrix = df.corr().abs()
# 选择相关度矩阵的上三角
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(np.bool))
# 寻找相关度大于 0.95 的特征列的索引
to_drop = [column for column in upper.columns if any(upper[column] > 0.95)]
# 丢弃特征
df.drop(df.columns[to_drop], axis=1)
| 0 | 2 | |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 2 | 0 |
| 2 | 3 | 1 |
| 3 | 4 | 0 |
| 4 | 5 | 1 |
| 5 | 6 | 0 |
| 6 | 7 | 1 |
| 7 | 8 | 0 |
| 8 | 9 | 1 |
递归特征消除
# 加载库
from sklearn.datasets import make_regression
from sklearn.feature_selection import RFECV
from sklearn import datasets, linear_model
import warnings
# 消除烦人但无害的警告
warnings.filterwarnings(action="ignore", module="scipy", message="^internal gelsd")
# 生成特征矩阵,目标向量和真实相关度
X, y = make_regression(n_samples = 10000,
n_features = 100,
n_informative = 2,
random_state = 1)
# 创建线性回归
ols = linear_model.LinearRegression()
# 创建递归特征消除器,按照 MSE 对特征评分
rfecv = RFECV(estimator=ols, step=1, scoring='neg_mean_squared_error')
# 拟合递归特征消除器
rfecv.fit(X, y)
# 递归特征消除
rfecv.transform(X)
'''
array([[ 0.00850799, 0.7031277 , -1.2416911 , -0.25651883, -0.10738769],
[-1.07500204, 2.56148527, 0.5540926 , -0.72602474, -0.91773159],
[ 1.37940721, -1.77039484, -0.59609275, 0.51485979, -1.17442094],
...,
[-0.80331656, -1.60648007, 0.37195763, 0.78006511, -0.20756972],
[ 0.39508844, -1.34564911, -0.9639982 , 1.7983361 , -0.61308782],
[-0.55383035, 0.82880112, 0.24597833, -1.71411248, 0.3816852 ]])
'''
# 最佳特征数量
rfecv.n_features_
# 5
方差阈值二元特征
from sklearn.feature_selection import VarianceThreshold
# 创建特征矩阵:
# 特征 0:80% 的类 0
# 特征 1:80% 的类 1
# 特征 2:60% 的类 0,40% 的类 1
X = [[0, 1, 0],
[0, 1, 1],
[0, 1, 0],
[0, 1, 1],
[1, 0, 0]]
在二元特征(即伯努利随机变量)中,方差计算如下:
](../img/tex-6959801ea921957ed53ddaab936b9409.gif)
其中 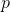 是类 1 观测的比例。 因此,通过设置
是类 1 观测的比例。 因此,通过设置 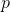 ,我们可以删除绝大多数观察是类 1 的特征。
,我们可以删除绝大多数观察是类 1 的特征。
# Run threshold by variance
thresholder = VarianceThreshold(threshold=(.75 * (1 - .75)))
thresholder.fit_transform(X)
'''
array([[0],
[1],
[0],
[1],
[0]])
'''
用于特征选择的方差阈值

from sklearn import datasets
from sklearn.feature_selection import VarianceThreshold
# 加载鸢尾花数据
iris = datasets.load_iris()
# 创建特征和目标
X = iris.data
y = iris.target
# 使用方差阈值 0.5 创建 VarianceThreshold 对象
thresholder = VarianceThreshold(threshold=.5)
# 应用方差阈值
X_high_variance = thresholder.fit_transform(X)
# 查看方差大于阈值的前五行
X_high_variance[0:5]
'''
array([[ 5.1, 1.4, 0.2],
[ 4.9, 1.4, 0.2],
[ 4.7, 1.3, 0.2],
[ 4.6, 1.5, 0.2],
[ 5\. , 1.4, 0.2]])
'''