8.6 可视化误差
译者:飞龙
本节是《Python 数据科学手册》(Python Data Science Handbook)的摘录。
对于任何科学测量,误差的准确计算几乎与数字本身的准确报告一样重要,甚至更重要。例如,假设我正在使用一些天体物理观测来估计哈勃常数,即宇宙膨胀率的局部测量值。我知道目前的文献显示,它是大约71 (km/s)/Mpc,我用我的方法测得的值为74 (km/s)/Mpc。这些值是否一致? 鉴于此信息,唯一正确的答案是:没有办法知道。
假设我用报告的不确定性来扩展这些信息:目前的文献显示它是71 ± 2.5 (km/s)/Mpc,我的方法测得的值为74 ± 5 (km/s)/Mpc。现在值是否一致? 这是一个可以定量回答的问题。
在数据和结果的可视化中,有效地显示这些误差,可以使图表传达更完整的信息。
基本的误差栏
可以使用单个 Matplotlib 函数调用,创建基本误差栏:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
x = np.linspace(0, 10, 50)
dy = 0.8
y = np.sin(x) + dy * np.random.randn(50)
plt.errorbar(x, y, yerr=dy, fmt='.k');
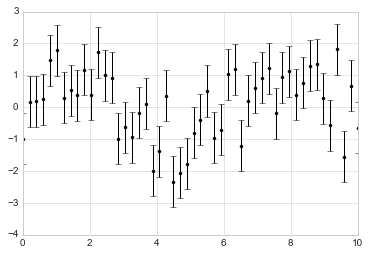
这里fmt是控制线和点外观的格式代码,与plt.plot中使用的简写语法相同,在“简单的折线图”和“简单的散点图”中概述。
除了这些基本选项之外,errorbar函数还有许多选项可以微调输出。使用这些附加选项,你可以轻松自定义误差栏绘图的美感。我经常发现它有用,特别是在拥挤的绘图中,使误差栏比点本身更浅:
plt.errorbar(x, y, yerr=dy, fmt='o', color='black',
ecolor='lightgray', elinewidth=3, capsize=0);
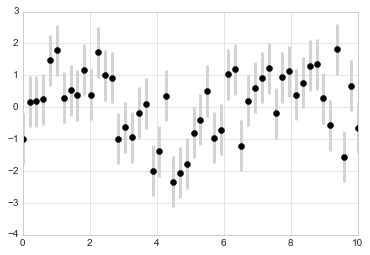
除了这些选项,你还可以指定水平误差栏(xerr),单侧误差栏和许多其他变体。对于可用选项的更多信息,请参阅plt.errorbar的文档字符串。
连续误差
在某些情况下,希望在连续数量上显示误差栏。虽然 Matplotlib 没有为这种类型的应用内置便利例程,但是将plt.plot和plt.fill_between之类的原语组合起来来获得有用的结果,是相对容易的。
在这里,我们将使用 Scikit-Learn API 执行简单的高斯过程回归(详细信息,请参阅“Scikit-Learn 简介”)。这是一种方法,使用不确定性的连续测量,将非常灵活的非参数函数拟合到数据。我们现在不会深入研究高斯过程回归的细节,而是专注于如何可视化这种连续误差测量:
from sklearn.gaussian_process import GaussianProcess
# 定义模型并绘制一些数据
model = lambda x: x * np.sin(x)
xdata = np.array([1, 3, 5, 6, 8])
ydata = model(xdata)
# 拟合高斯过程
gp = GaussianProcess(corr='cubic', theta0=1e-2, thetaL=1e-4, thetaU=1E-1,
random_start=100)
gp.fit(xdata[:, np.newaxis], ydata)
xfit = np.linspace(0, 10, 1000)
yfit, MSE = gp.predict(xfit[:, np.newaxis], eval_MSE=True)
dyfit = 2 * np.sqrt(MSE) # 2*sigma ~ 95% confidence region
我们现在有xfit,yfit和dyfit,它们对数据的连续拟合进行抽样。我们可以将这些传递给上面的plt.errorbar函数,但是我们真的不想绘制 1000 个点和 1000 个误差栏。相反,我们可以使用浅色的plt.fill_between函数来显示这个连续误差:
# 可视化结果
plt.plot(xdata, ydata, 'or')
plt.plot(xfit, yfit, '-', color='gray')
plt.fill_between(xfit, yfit - dyfit, yfit + dyfit,
color='gray', alpha=0.2)
plt.xlim(0, 10);
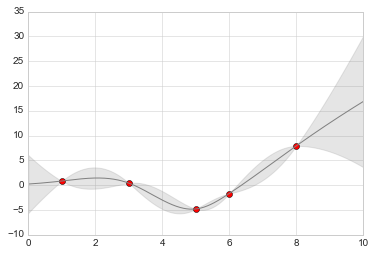
注意我们在这里使用fill_between函数做了什么:我们传递一个x值,然后是y下界,然后是y上面,结果就是之间的区域被填充了。
得到的图形可以用于非常直观地了解高斯过程回归算法正在做什么:在测量数据点附近的区域中,模型受到强烈约束,这反映在较小的模型误差中。在远离测量数据点的区域中,模型不受强烈约束,并且模型误差增加。
对于plt.fill_between()(以及密切相关的plt.fill()函数)中,可用选项的更多信息,请参阅函数的文档字符串或 Matplotlib 文档。
最后,如果这和你的品味相比,看起来有点太低了,请参考“可视化与 Seaborn”,其中我们讨论了 Seaborn 包,它有更简化的 API,用于可视化这种类型 的连续误差栏。