2.3 Sequences

A sequence is an ordered collection of data values. Unlike a pair, which has exactly two elements, a sequence can have an arbitrary (but finite) number of ordered elements.

The sequence is a powerful, fundamental abstraction in computer science. For example, if we have sequences, we can list every student at Berkeley, or every university in the world, or every student in every university. We can list every class ever taken, every assignment ever completed, every grade ever received. The sequence abstraction enables the thousands of data-driven programs that impact our lives every day.

A sequence is not a particular abstract data type, but instead a collection of behaviors that different types share. That is, there are many kinds of sequences, but they all share certain properties. In particular,

Length. A sequence has a finite length.

Element selection. A sequence has an element corresponding to any non-negative integer index less than its length, starting at 0 for the first element.

Unlike an abstract data type, we have not stated how to construct a sequence. The sequence abstraction is a collection of behaviors that does not fully specify a type (i.e., with constructors and selectors), but may be shared among several types. Sequences provide a layer of abstraction that may hide the details of exactly which sequence type is being manipulated by a particular program.

In this section, we develop a particular abstract data type that can implement the sequence abstraction. We then introduce built-in Python types that also implement the same abstraction.

2.3.1 Nested Pairs

For rational numbers, we paired together two integer objects using a two-element tuple, then showed that we could implement pairs just as well using functions. In that case, the elements of each pair we constructed were integers. However, like expressions, tuples can nest. Either element of a pair can itself be a pair, a property that holds true for either method of implementing a pair that we have seen: as a tuple or as a dispatch function.

A standard way to visualize a pair --- in this case, the pair (1,2) --- is called box-and-pointer notation. Each value, compound or primitive, is depicted as a pointer to a box. The box for a primitive value contains a representation of that value. For example, the box for a number contains a numeral. The box for a pair is actually a double box: the left part contains (an arrow to) the first element of the pair and the right part contains the second.

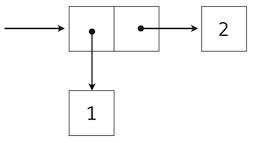
This Python expression for a nested tuple,

>>> ((1, 2), (3, 4))
((1, 2), (3, 4))

would have the following structure.

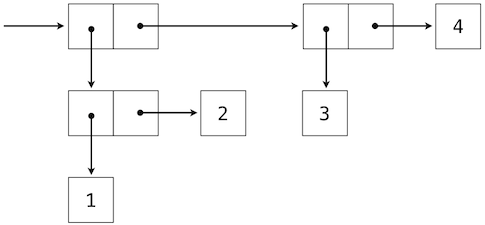
Our ability to use tuples as the elements of other tuples provides a new means of combination in our programming language. We call the ability for tuples to nest in this way a closure property of the tuple data type. In general, a method for combining data values satisfies the closure property if the result of combination can itself be combined using the same method. Closure is the key to power in any means of combination because it permits us to create hierarchical structures --- structures made up of parts, which themselves are made up of parts, and so on. We will explore a range of hierarchical structures in Chapter 3. For now, we consider a particularly important structure.

2.3.2 Recursive Lists

We can use nested pairs to form lists of elements of arbitrary length, which will allow us to implement the sequence abstraction. The figure below illustrates the structure of the recursive representation of a four-element list: 1, 2, 3, 4.

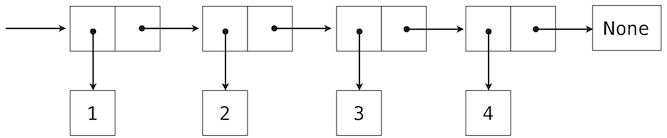
The list is represented by a chain of pairs. The first element of each pair is an element in the list, while the second is a pair that represents the rest of the list. The second element of the final pair is None, which indicates that the list has ended. We can construct this structure using a nested tuple literal:

>>> (1, (2, (3, (4, None))))
(1, (2, (3, (4, None))))

This nested structure corresponds to a very useful way of thinking about sequences in general, which we have seen before in the execution rules of the Python interpreter. A non-empty sequence can be decomposed into:

• its first element, and
• the rest of the sequence.

The rest of a sequence is itself a (possibly empty) sequence. We call this view of sequences recursive, because sequences contain other sequences as their second component.

Since our list representation is recursive, we will call it an rlist in our implementation, so as not to confuse it with the built-in list type in Python that we will introduce later in this chapter. A recursive list can be constructed from a first element and the rest of the list. The value None represents an empty recursive list.

>>> empty_rlist = None
>>> def make_rlist(first, rest):
        """Make a recursive list from its first element and the rest."""
        return (first, rest)

>>> def first(s):
        """Return the first element of a recursive list s."""
        return s[0]

>>> def rest(s):
        """Return the rest of the elements of a recursive list s."""
        return s[1]

These two selectors, one constructor, and one constant together implement the recursive list abstract data type. The single behavior condition for a recursive list is that, like a pair, its constructor and selectors are inverse functions.

• If a recursive list s was constructed from element f and list r, then first(s) returns f, and rest(s) returns r.

We can use the constructor and selectors to manipulate recursive lists.

>>> counts = make_rlist(1, make_rlist(2, make_rlist(3, make_rlist(4, empty_rlist))))
>>> first(counts)
1
>>> rest(counts)
(2, (3, (4, None)))

Recall that we were able to represent pairs using functions, and therefore we can represent recursive lists using functions as well.

The recursive list can store a sequence of values in order, but it does not yet implement the sequence abstraction. Using the abstract data type we have defined, we can implement the two behaviors that characterize a sequence: length and element selection.

>>> def len_rlist(s):
        """Return the length of recursive list s."""
        length = 0
        while s != empty_rlist:
            s, length = rest(s), length + 1
        return length

>>> def getitem_rlist(s, i):
        """Return the element at index i of recursive list s."""
        while i > 0:
            s, i = rest(s), i - 1
        return first(s)

Now, we can manipulate a recursive list as a sequence:

>>> len_rlist(counts)
4
>>> getitem_rlist(counts, 1)  # The second item has index 1
2

Both of these implementations are iterative. They peel away each layer of nested pair until the end of the list (in len_rlist) or the desired element (in getitem_rlist) is reached.

The series of environment diagrams below illustrate the iterative process by which getitem_rlist finds the element 2 at index 1 in the recursive list. First, the function getitem_rlist is called, creating a local frame.

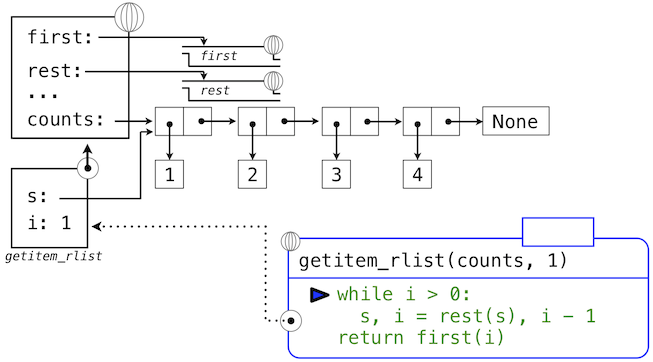
The expression in the while header evaluates to true, which causes the assignment statement in the while suite to be executed.

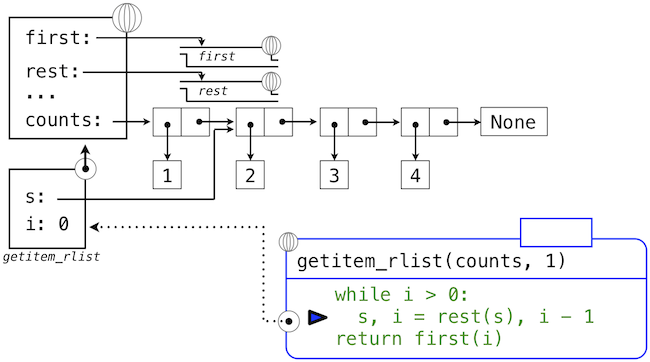
In this case, the local name s now refers to the sub-list that begins with the second element of the original list. Evaluating the while header expression now yields a false value, and so Python evaluates the expression in the return statement on the final line of getitem_rlist.

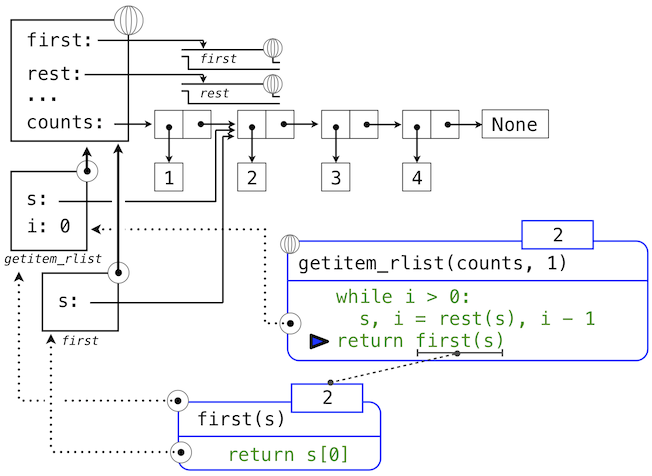
This final environment diagram shows the local frame for the call to first, which contains the name s bound to that same sub-list. The first function selects the value 2 and returns it, completing the call to getitem_rlist.

This example demonstrates a common pattern of computation with recursive lists, where each step in an iteration operates on an increasingly shorter suffix of the original list. This incremental processing to find the length and elements of a recursive list does take some time to compute. (In Chapter 3, we will learn to characterize the computation time of iterative functions like these.) Python's built-in sequence types are implemented in a different way that does not have a large computational cost for computing the length of a sequence or retrieving its elements.

The way in which we construct recursive lists is rather verbose. Fortunately, Python provides a variety of built-in sequence types that provide both the versatility of the sequence abstraction, as well as convenient notation.

2.3.3 Tuples II

In fact, the tuple type that we introduced to form primitive pairs is itself a full sequence type. Tuples provide substantially more functionality than the pair abstract data type that we implemented functionally.

Tuples can have arbitrary length, and they exhibit the two principal behaviors of the sequence abstraction: length and element selection. Below, digits is a tuple with four elements.

>>> digits = (1, 8, 2, 8)
>>> len(digits)
4
>>> digits[3]
8

Additionally, tuples can be added together and multiplied by integers. For tuples, addition and multiplication do not add or multiply elements, but instead combine and replicate the tuples themselves. That is, the add function in the operator module (and the + operator) returns a new tuple that is the conjunction of the added arguments. The mul function in operator (and the * operator) can take an integer k and a tuple and return a new tuple that consists of k copies of the tuple argument.

>>> (2, 7) + digits * 2
(2, 7, 1, 8, 2, 8, 1, 8, 2, 8)

Mapping. A powerful method of transforming one tuple into another is by applying a function to each element and collecting the results. This general form of computation is called mapping a function over a sequence, and corresponds to the built-in function map. The result of map is an object that is not itself a sequence, but can be converted into a sequence by calling tuple, the constructor function for tuples.

>>> alternates = (-1, 2, -3, 4, -5)
>>> tuple(map(abs, alternates))
(1, 2, 3, 4, 5)

The map function is important because it relies on the sequence abstraction: we do not need to be concerned about the structure of the underlying tuple; only that we can access each one of its elements individually in order to pass it as an argument to the mapped function (abs, in this case).

2.3.4 Sequence Iteration

Mapping is itself an instance of a general pattern of computation: iterating over all elements in a sequence. To map a function over a sequence, we do not just select a particular element, but each element in turn. This pattern is so common that Python has an additional control statement to process sequential data: the for statement.

Consider the problem of counting how many times a value appears in a sequence. We can implement a function to compute this count using a while loop.

>>> def count(s, value):
        """Count the number of occurrences of value in sequence s."""
        total, index = 0, 0
        while index < len(s):
            if s[index] == value:
                total = total + 1
            index = index + 1
        return total

>>> count(digits, 8)
2

The Python for statement can simplify this function body by iterating over the element values directly, without introducing the name index at all. For example (pun intended), we can write:

>>> def count(s, value):
        """Count the number of occurrences of value in sequence s."""
        total = 0
        for elem in s:
            if elem == value:
                total = total + 1
        return total

>>> count(digits, 8)
2

A for statement consists of a single clause with the form:

for <name> in <expression>:
    <suite>

A for statement is executed by the following procedure:

1. Evaluate the header <expression>, which must yield an iterable value.
2. For each element value in that sequence, in order:
   1. Bind <name> to that value in the local environment.
   2. Execute the <suite>.

Step 1 refers to an iterable value. Sequences are iterable, and their elements are considered in their sequential order. Python does include other iterable types, but we will focus on sequences for now; the general definition of the term "iterable" appears in the section on iterators in Chapter 4.

An important consequence of this evaluation procedure is that <name> will be bound to the last element of the sequence after the for statement is executed. The for loop introduces yet another way in which the local environment can be updated by a statement.

Sequence unpacking. A common pattern in programs is to have a sequence of elements that are themselves sequences, but all of a fixed length. For statements may include multiple names in their header to "unpack" each element sequence into its respective elements. For example, we may have a sequence of pairs (that is, two-element tuples),

>>> pairs = ((1, 2), (2, 2), (2, 3), (4, 4))

and wish to find the number of pairs that have the same first and second element.

>>> same_count = 0

The following for statement with two names in its header will bind each name x and y to the first and second elements in each pair, respectively.

>>> for x, y in pairs:
        if x == y:
            same_count = same_count + 1

>>> same_count
2

This pattern of binding multiple names to multiple values in a fixed-length sequence is called sequence unpacking; it is the same pattern that we see in assignment statements that bind multiple names to multiple values.

Ranges. A range is another built-in type of sequence in Python, which represents a range of integers. Ranges are created with the range function, which takes two integer arguments: the first number and one beyond the last number in the desired range.

>>> range(1, 10)  # Includes 1, but not 10
range(1, 10)

Calling the tuple constructor on a range will create a tuple with the same elements as the range, so that the elements can be easily inspected.

>>> tuple(range(5, 8))
(5, 6, 7)

If only one argument is given, it is interpreted as one beyond the last value for a range that starts at 0.

>>> tuple(range(4))
(0, 1, 2, 3)

Ranges commonly appear as the expression in a for header to specify the number of times that the suite should be executed:

>>> total = 0
>>> for k in range(5, 8):
        total = total + k

>>> total
18

A common convention is to use a single underscore character for the name in the for header if the name is unused in the suite:

>>> for _ in range(3):
        print('Go Bears!')

Go Bears!
Go Bears!
Go Bears!

Note that an underscore is just another name in the environment as far as the interpreter is concerned, but has a conventional meaning among programmers that indicates the name will not appear in any expressions.

2.3.5 Sequence Abstraction

We have now introduced two types of native data types that implement the sequence abstraction: tuples and ranges. Both satisfy the conditions with which we began this section: length and element selection. Python includes two more behaviors of sequence types that extend the sequence abstraction.

Membership. A value can be tested for membership in a sequence. Python has two operators in and not in that evaluate to True or False depending on whether an element appears in a sequence.

>>> digits
(1, 8, 2, 8)
>>> 2 in digits
True
>>> 1828 not in digits
True

All sequences also have methods called index and count, which return the index of (or count of) a value in a sequence.

Slicing. Sequences contain smaller sequences within them. We observed this property when developing our nested pairs implementation, which decomposed a sequence into its first element and the rest. A slice of a sequence is any span of the original sequence, designated by a pair of integers. As with the range constructor, the first integer indicates the starting index of the slice and the second indicates one beyond the ending index.

In Python, sequence slicing is expressed similarly to element selection, using square brackets. A colon separates the starting and ending indices. Any bound that is omitted is assumed to be an extreme value: 0 for the starting index, and the length of the sequence for the ending index.

>>> digits[0:2]
(1, 8)
>>> digits[1:]
(8, 2, 8)

Enumerating these additional behaviors of the Python sequence abstraction gives us an opportunity to reflect upon what constitutes a useful data abstraction in general. The richness of an abstraction (that is, how many behaviors it includes) has consequences. For users of an abstraction, additional behaviors can be helpful. On the other hand, satisfying the requirements of a rich abstraction with a new data type can be challenging. To ensure that our implementation of recursive lists supported these additional behaviors would require some work. Another negative consequence of rich abstractions is that they take longer for users to learn.

Sequences have a rich abstraction because they are so ubiquitous in computing that learning a few complex behaviors is justified. In general, most user-defined abstractions should be kept as simple as possible.

Further reading. Slice notation admits a variety of special cases, such as negative starting values, ending values, and step sizes. A complete description appears in the subsection called slicing a list in Dive Into Python 3. In this chapter, we will only use the basic features described above.

2.3.6 Strings

Text values are perhaps more fundamental to computer science than even numbers. As a case in point, Python programs are written and stored as text. The native data type for text in Python is called a string, and corresponds to the constructor str.

There are many details of how strings are represented, expressed, and manipulated in Python. Strings are another example of a rich abstraction, one which requires a substantial commitment on the part of the programmer to master. This section serves as a condensed introduction to essential string behaviors.

String literals can express arbitrary text, surrounded by either single or double quotation marks.

>>> 'I am string!'
'I am string!'
>>> "I've got an apostrophe"
"I've got an apostrophe"
>>> '您好'
'您好'

We have seen strings already in our code, as docstrings, in calls to print, and as error messages in assert statements.

Strings satisfy the two basic conditions of a sequence that we introduced at the beginning of this section: they have a length and they support element selection.

>>> city = 'Berkeley'
>>> len(city)
8
>>> city[3]
'k'

The elements of a string are themselves strings that have only a single character. A character is any single letter of the alphabet, punctuation mark, or other symbol. Unlike many other programming languages, Python does not have a separate character type; any text is a string, and strings that represent single characters have a length of 1.

Like tuples, strings can also be combined via addition and multiplication.

>>> 'Berkeley' + ', CA'
'Berkeley, CA'
>>> 'Shabu ' * 2
'Shabu Shabu '

Membership. The behavior of strings diverges from other sequence types in Python. The string abstraction does not conform to the full sequence abstraction that we described for tuples and ranges. In particular, the membership operator in applies to strings, but has an entirely different behavior than when it is applied to sequences. It matches substrings rather than elements.

>>> 'here' in "Where's Waldo?"
True

Likewise, the count and index methods on strings take substrings as arguments, rather than single-character elements. The behavior of count is particularly nuanced; it counts the number of non-overlapping occurrences of a substring in a string.

>>> 'Mississippi'.count('i')
4
>>> 'Mississippi'.count('issi')
1

Multiline Literals. Strings aren't limited to a single line. Triple quotes delimit string literals that span multiple lines. We have used this triple quoting extensively already for docstrings.

>>> """The Zen of Python
claims, Readability counts.
Read more: import this."""
'The Zen of Python\nclaims, "Readability counts."\nRead more: import this.'

In the printed result above, the \n (pronounced "backslash en") is a single element that represents a new line. Although it appears as two characters (backslash and "n"), it is considered a single character for the purposes of length and element selection.

String Coercion. A string can be created from any object in Python by calling the str constructor function with an object value as its argument. This feature of strings is useful for constructing descriptive strings from objects of various types.

>>> str(2) + ' is an element of ' + str(digits)
'2 is an element of (1, 8, 2, 8)'

The mechanism by which a single str function can apply to any type of argument and return an appropriate value is the subject of the later section on generic functions.

Methods. The behavior of strings in Python is extremely productive because of a rich set of methods for returning string variants and searching for contents. A few of these methods are introduced below by example.

>>> '1234'.isnumeric()
True
>>> 'rOBERT dE nIRO'.swapcase()
'Robert De Niro'
>>> 'snakeyes'.upper().endswith('YES')
True

Further reading. Encoding text in computers is a complex topic. In this chapter, we will abstract away the details of how strings are represented. However, for many applications, the particular details of how strings are encoded by computers is essential knowledge. Sections 4.1-4.3 of Dive Into Python 3 provides a description of character encodings and Unicode.

2.3.7 Conventional Interfaces

In working with compound data, we've stressed how data abstraction permits us to design programs without becoming enmeshed in the details of data representations, and how abstraction preserves for us the flexibility to experiment with alternative representations. In this section, we introduce another powerful design principle for working with data structures --- the use of conventional interfaces.

A conventional interface is a data format that is shared across many modular components, which can be mixed and matched to perform data processing. For example, if we have several functions that all take a sequence as an argument and return a sequence as a value, then we can apply each to the output of the next in any order we choose. In this way, we can create a complex process by chaining together a pipeline of functions, each of which is simple and focused.

This section has a dual purpose: to introduce the idea of organizing a program around a conventional interface, and to demonstrate examples of modular sequence processing.

Consider these two problems, which appear at first to be related only in their use of sequences:

1. Sum the even members of the first n Fibonacci numbers.
2. List the letters in the acronym for a name, which includes the first letter of each capitalized word.

These problems are related because they can be decomposed into simple operations that take sequences as input and yield sequences as output. Moreover, those operations are instances of general methods of computation over sequences. Let's consider the first problem. It can be decomposed into the following steps:

 enumerate     map    filter  accumulate
-----------    ---    ------  ----------
naturals(n)    fib    iseven     sum

The fib function below computes Fibonacci numbers (now updated from the definition in Chapter 1 with a for statement),

>>> def fib(k):
        """Compute the kth Fibonacci number."""
        prev, curr = 1, 0  # curr is the first Fibonacci number.
        for _ in range(k - 1):
             prev, curr = curr, prev + curr
        return curr

and a predicate iseven can be defined using the integer remainder operator, %.

>>> def iseven(n):
        return n % 2 == 0

The functions map and filter are operations on sequences. We have already encountered map, which applies a function to each element in a sequence and collects the results. The filter function takes a sequence and returns those elements of a sequence for which a predicate is true. Both of these functions return intermediate objects, map and filter objects, which are iterable objects that can be converted into tuples or summed.

>>> nums = (5, 6, -7, -8, 9)
>>> tuple(filter(iseven, nums))
(6, -8)
>>> sum(map(abs, nums))
35

Now we can implement even_fib, the solution to our first problem, in terms of map, filter, and sum.

>>> def sum_even_fibs(n):
        """Sum the first n even Fibonacci numbers."""
        return sum(filter(iseven, map(fib, range(1, n+1))))

>>> sum_even_fibs(20)
3382

Now, let's consider the second problem. It can also be decomposed as a pipeline of sequence operations that include map and filter:

enumerate  filter   map   accumulate
---------  ------  -----  ----------
  words    iscap   first    tuple

The words in a string can be enumerated via the split method of a string object, which by default splits on spaces.

>>> tuple('Spaces between words'.split())
('Spaces', 'between', 'words')

The first letter of a word can be retrieved using the selection operator, and a predicate that determines if a word is capitalized can be defined using the built-in predicate isupper.

>>> def first(s):
        return s[0]

>>> def iscap(s):
        return len(s) > 0 and s[0].isupper()

At this point, our acronym function can be defined via map and filter.

>>> def acronym(name):
        """Return a tuple of the letters that form the acronym for name."""
        return tuple(map(first, filter(iscap, name.split())))

>>> acronym('University of California Berkeley Undergraduate Graphics Group')
('U', 'C', 'B', 'U', 'G', 'G')

These similar solutions to rather different problems show how to combine general components that operate on the conventional interface of a sequence using the general computational patterns of mapping, filtering, and accumulation. The sequence abstraction allows us to specify these solutions concisely.

Expressing programs as sequence operations helps us design programs that are modular. That is, our designs are constructed by combining relatively independent pieces, each of which transforms a sequence. In general, we can encourage modular design by providing a library of standard components together with a conventional interface for connecting the components in flexible ways.

Generator expressions. The Python language includes a second approach to processing sequences, called generator expressions. which provide similar functionality to map and filter, but may require fewer function definitions.

Generator expressions combine the ideas of filtering and mapping together into a single expression type with the following form:

<map expression> for <name> in <sequence expression> if <filter expression>

To evaluate a generator expression, Python evaluates the <sequence expression>, which must return an iterable value. Then, for each element in order, the element value is bound to <name>, the filter expression is evaluated, and if it yields a true value, the map expression is evaluated.

The result value of evaluating a generator expression is itself an iterable value. Accumulation functions like tuple, sum, max, and min can take this returned object as an argument.

>>> def acronym(name):
        return tuple(w[0] for w in name.split() if iscap(w))

>>> def sum_even_fibs(n):
        return sum(fib(k) for k in range(1, n+1) if fib(k) % 2 == 0)

Generator expressions are specialized syntax that utilizes the conventional interface of iterable values, such as sequences. These expressions subsume most of the functionality of map and filter, but avoid actually creating the function values that are applied (or, incidentally, creating the environment frames required to apply those functions).

Reduce. In our examples we used specific functions to accumulate results, either tuple or sum. Functional programming languages (including Python) include general higher-order accumulators that go by various names. Python includes reduce in the functools module, which applies a two-argument function cumulatively to the elements of a sequence from left to right, to reduce a sequence to a value. The following expression computes 5 factorial.

>>> from operator import mul
>>> from functools import reduce
>>> reduce(mul, (1, 2, 3, 4, 5))
120

Using this more general form of accumulation, we can also compute the product of even Fibonacci numbers, in addition to the sum, using sequences as a conventional interface.

>>> def product_even_fibs(n):
        """Return the product of the first n even Fibonacci numbers, except 0."""
        return reduce(mul, filter(iseven, map(fib, range(2, n+1))))

>>> product_even_fibs(20)
123476336640

The combination of higher order procedures corresponding to map, filter, and reduce will appear again in Chapter 4, when we consider methods for distributing computation across multiple computers.