量化分析师的Python日记【第13天 Q Quant兵器谱之偏微分方程3】
来源:https://uqer.io/community/share/555dc9e8f9f06c6c7404f96e
欢迎来到 Black - Scholes — Merton 的世界!本篇中我们将使用在第11天学习到的知识应用到这个金融学的具体方程之上!
import numpy as np
import math
import seaborn as sns
from matplotlib import pylab
font.set_size(15)
1. 问题的提出
BSM模型可以设置为如下的偏微分方差初值问题:
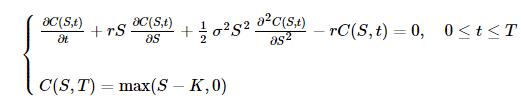
做变量替换τ=T−t,并且设置上下边界条件:
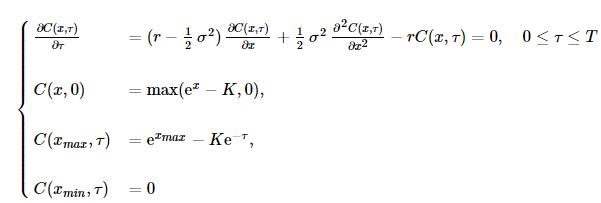
2. 算法
按照之前介绍的隐式差分格式的方法,用离散差分格式代替连续微分:
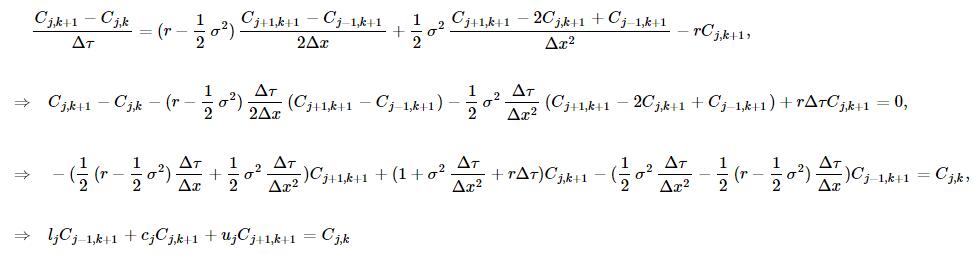
其中
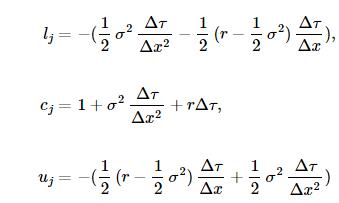
以上即为差分方程组。
这里有些细节需要处理,就是左右边界条件,我们这里使用Dirichlet边界条件,则:
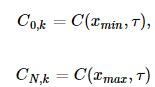
3.实现
import scipy as sp
from scipy.linalg import solve_banded
描述BSM方程结构的类:BSMModel
class BSMModel:
def __init__(self, s0, r, sigma):
self.s0 = s0
self.x0 = math.log(s0)
self.r = r
self.sigma = sigma
def log_expectation(self, T):
return self.x0 + (self.r - 0.5 * self.sigma * self.sigma) * T
def expectation(self, T):
return math.exp(self.log_expectation(T))
def x_max(self, T):
return self.log_expectation(T) + 4.0 * self.sigma * math.sqrt(T)
def x_min(self, T):
return self.log_expectation(T) - 4.0 * self.sigma * math.sqrt(T)
描述我们这里设计到的产品的类:CallOption
class CallOption:
def __init__(self, strike):
self.k = strike
def ic(self, spot):
return max(spot - self.k, 0.0)
def bcl(self, spot, tau, model):
return 0.0
def bcr(self, spot, tau, model):
return spot - math.exp(-model.r*tau) * self.k
完整的隐式格式:BSMScheme
class BSMScheme:
def __init__(self, model, payoff, T, M, N):
self.model = model
self.T = T
self.M = M
self.N = N
self.dt = self.T / self.M
self.payoff = payoff
self.x_min = model.x_min(self.T)
self.x_max = model.x_max(self.T)
self.dx = (self.x_max - self.x_min) / self.N
self.C = np.zeros((self.N+1, self.M+1)) # 全部网格
self.xArray = np.linspace(self.x_min, self.x_max, self.N+1)
self.C[:,0] = map(self.payoff.ic, np.exp(self.xArray))
sigma_square = self.model.sigma*self.model.sigma
r = self.model.r
self.l_j = -(0.5*sigma_square*self.dt/self.dx/self.dx - 0.5 * (r - 0.5 * sigma_square)*self.dt/self.dx)
self.c_j = 1.0 + sigma_square*self.dt/self.dx/self.dx + r*self.dt
self.u_j = -(0.5*sigma_square*self.dt/self.dx/self.dx + 0.5 * (r - 0.5 * sigma_square)*self.dt/self.dx)
def roll_back(self):
for k in range(0, self.M):
udiag = np.ones(self.N-1) * self.u_j
ldiag = np.ones(self.N-1) * self.l_j
cdiag = np.ones(self.N-1) * self.c_j
mat = np.zeros((3,self.N-1))
mat[0,:] = udiag
mat[1,:] = cdiag
mat[2,:] = ldiag
rhs = np.copy(self.C[1:self.N,k])
# 应用左端边值条件
v1 = self.payoff.bcl(math.exp(self.x_min), (k+1)*self.dt, self.model)
rhs[0] -= self.l_j * v1
# 应用右端边值条件
v2 = self.payoff.bcr(math.exp(self.x_max), (k+1)*self.dt, self.model)
rhs[-1] -= self.u_j * v2
x = solve_banded((1,1), mat, rhs)
self.C[1:self.N, k+1] = x
self.C[0][k+1] = v1
self.C[self.N][k+1] = v2
def mesh_grids(self):
tArray = np.linspace(0, self.T, self.M+1)
tGrids, xGrids = np.meshgrid(tArray, self.xArray)
return tGrids, xGrids
应用在一起:
model = BSMModel(100.0, 0.05, 0.2)
payoff = CallOption(105.0)
scheme = BSMScheme(model, payoff, 5.0, 100, 300)
scheme.roll_back()
from matplotlib import pylab
pylab.figure(figsize=(12,8))
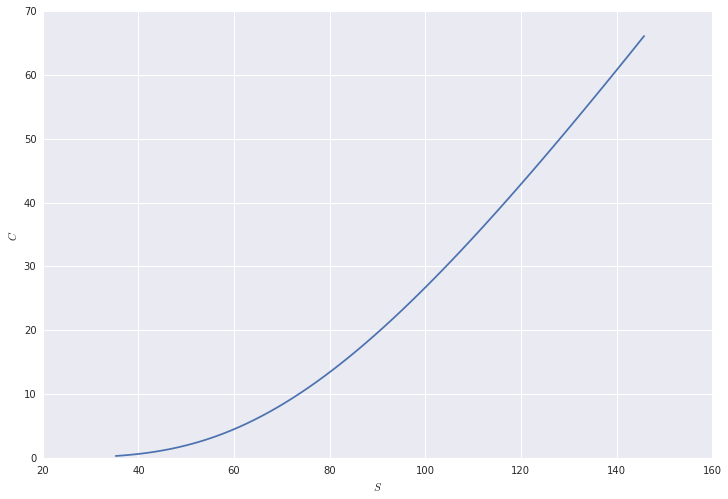
pylab.plot(np.exp(scheme.xArray)[50:170], scheme.C[50:170,-1])
pylab.xlabel('$S$')
pylab.ylabel('$C$')
<matplotlib.text.Text at 0x76ea7d0>
4. 收敛性测试
首先使用BSM模型的解析解获得精确解:
analyticPrice = BSMPrice(1, 105., 100., 0.05, 0.0, 0.2, 5.)
analyticPrice
| price | delta | gamma | vega | rho | theta | |
|---|---|---|---|---|---|---|
| 1 | 26.761844 | 0.749694 | 0.00711 | 71.10319 | 241.037549 | -3.832439 |
我们固定时间方向网格数为3000,分别计算不同S网格数情形下的结果:
xSteps = range(50,300,10)
finiteResult = []
for xStep in xSteps:
model = BSMModel(100.0, 0.05, 0.2)
payoff = CallOption(105.0)
scheme = BSMScheme(model, payoff, 5.0, 3000, xStep)
scheme.roll_back()
interp = CubicNaturalSpline(np.exp(scheme.xArray), scheme.C[:,-1])
price = interp(100.0)
finiteResult.append(price)
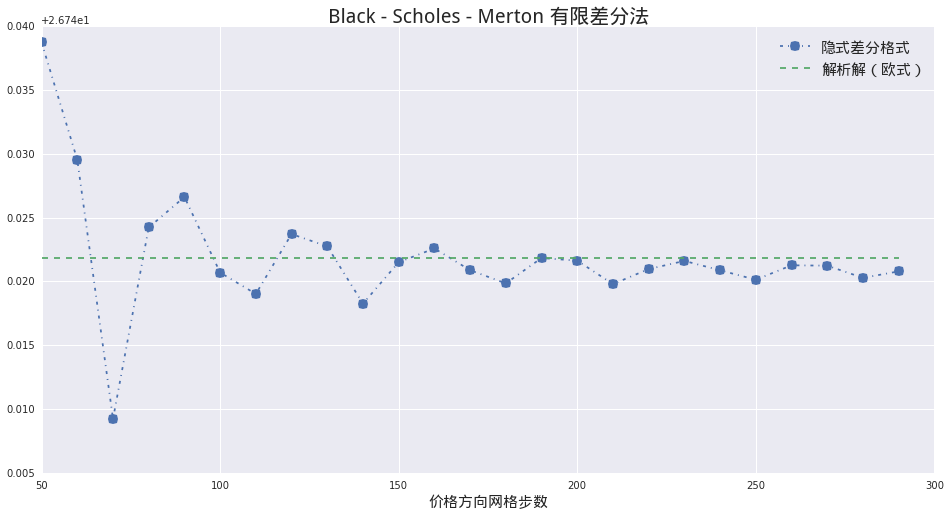
我们可以画下收敛图:
anyRes = [analyticPrice['price'][1]] * len(xSteps)
pylab.figure(figsize = (16,8))
pylab.plot(xSteps, finiteResult, '-.', marker = 'o', markersize = 10)
pylab.plot(xSteps, anyRes, '--')
pylab.legend([u'隐式差分格式', u'解析解(欧式)'], prop = font)
pylab.xlabel(u'价格方向网格步数', fontproperties = font)
pylab.title(u'Black - Scholes - Merton 有限差分法', fontproperties = font, fontsize = 20)
<matplotlib.text.Text at 0x7857bd0>