3.3.1 传统的错误检测方法

如何提高程序的健壮性？关键显然在于如何发现运行时错误并加以处理。顾名思义，运行时错误是在程序运行时才暴露的，很难在静态的编译阶段检查出来。传统编程方法中常利用 if 语句来检测可能导致异常发生的条件，以期发现并处理错误。具体的检测方式有两种，一种是在执行任务之前检测条件，另一种是执行任务之后检测返回状态码或错误码。

作为例子，我们来编写一个求解一元二次方程的程序。利用初等代数知识，我们知道一元二次方程 ax2+bx+c=0 的两个根是：

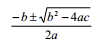
据此很容易写出下面这个程序：

【程序 3.5】eg3_5.py

import math
a, b, c = input("Enter the coefficients (a, b, c): ") 
discRoot = math.sqrt(b * b - 4 * a * c)
root1 = (-b + discRoot) / (2 * a) 
root2 = (-b - discRoot) / (2 * a)
print "The solutions are:", root1, root2

本程序先由用户输入一元二次方程的三个系数，然后利用公式算出两个根，并显示结果。这个版本看上去很直接了当，似乎符合预期的功能，但实际上这个版本很有问题。下面我们来运行这个程序：

>>> import eg3_5
Enter the coefficients (a, b, c): 1,2,3
Traceback (most recent call last):
File "<pyshell#0>", line 1, in <module> import eg3_x
File "eg3_x.py", line 3, in <module> discRoot = math.sqrt(b * b - 4 * a * c)
ValueError: math domain error

由于用户输入的系数 1、2、3 使得一元二次方程的判别式 b2 - 4ac 小于零，因此当程序运行到调用 math.sqrt 函数时导致错误，程序崩溃并输出上面这一堆错误信息。作为专业的程序员，对这里发生的一切自然能理解，但作为普通的用户，看到这些天书般的的错误信息时除了抱怨程序不好用，还能怎么办呢？

为了增强程序 3.5 的健壮性，可以用 if 语句来检查判别式的值，以便区别处理方程有实数根和无实数根的两种情形，避免在无实数根的情况下崩溃。改进版本如下：

【程序 3.6】eg3_6.py

import math
a, b, c = input("Enter the coefficients (a, b, c): ") 
discrim = b * b - 4 * a * c
if discrim &gt;= 0:
    discRoot = math.sqrt(discrim)
    root1 = (-b + discRoot) / (2 * a) 
    root2 = (-b - discRoot) / (2 * a)
    print "The solutions are:", root1, root2 
else:
    print "The equation has no real roots!"

从程序中可见，仅当判别式 discrim 大于等于 0 时，才去调用 math.sqrt 函数求其平方根，这样 sqrt 不会出错，从而避免了程序崩溃；当 discrim 为负数时，并不调用 sqrt，而是向用户显示一些信息，告诉用户发生了什么，程序同样能正常结束。

下面分别测试程序 3.6 对两种情形的判别式的执行效果：

>>> import eg3_6
Enter the coefficients (a, b, c): 1,2,3
The equation has no real roots!
>>> reload(eg3_6)①
Enter the coefficients (a, b, c): 1,3,2
The solutions are: -1.0 -2.0

从结果可见程序 3.6 确实达到了预期的目的，健壮性得到了增强。

像程序 3.6 这样利用 if 语句来检测可能的出错条件，以阻止可能导致错误的语句的执行，这是一种常用的错误检测方式。下面介绍另一种错误检测方式。

很多时候要执行的语句实际上是函数调用②，被调用的函数可能是我们自己写的，也可能是标准函数库里定义的。函数作为一个具有相对独立性的程序块，一般都有自己的错误检测代码，并根据执行是否正常而返回不同的“错误码”给调用者。这样，函数的调用者可以无条件地调用函数，然后根据函数返回的错误码来了解函数的执行情况，并基于此来决定下一步行动。例如，假设有一个求平方根的函数 robustSqrt 在参数为负数时返回错误码-1（由于实数的平方根总是正数，返回-1 就表明发生了异常）：

def robustSqrt(x): 
    if x < 0:
        return -1 
    else:
        return math.sqrt(x)

那我们就可以不必先检测判别式的正负，而是直接调用 robustSqrt，并通过它的返回值来检测是否发生了异常。示例代码片段如下：

discRoot = robustSqrt(b * b – 4 * a * c) 
if discRoot < 0:
    print "The equation has no real roots!" 
else:
    root1 = (-b + discRoot) / (2 * a) 
    root2 = (-b – discRoot) / (2 * a)
    print "The solutions are:", root1, root2

与程序 3.6 中的错误检测代码相比，上面这种错误检测代码更可取。理由是：函数就像一个提供特定功能的“黑盒”，我们只需调用其功能，不需了解其内部细节，因此让函数自己在内部进行错误检测更符合“黑盒”原则。程序 3.6 中的错误检测建立在对函数 math.sqrt 内部执行细节（即负数导致崩溃）的了解之上，因而不符合“黑盒”原则。

① reload 函数用于重新运行一个已成功导入的模块。

② 关于函数，详见第 4 章。