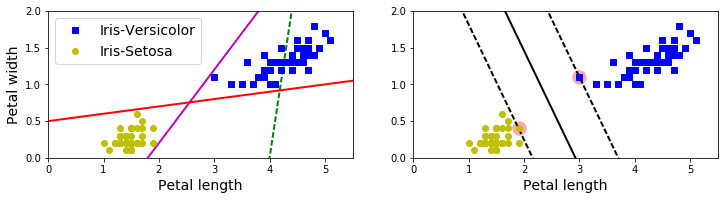
SVM Classification (Linear)

Well suited for complex, small/medium dataset classification.

%matplotlib inline
import matplotlib.pyplot as plt

# Large margin classification:

from sklearn.svm import SVC
from sklearn import datasets

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = iris["target"]

setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]

# SVM Classifier model
svm_clf = SVC(kernel="linear", C=float("inf"))
svm_clf.fit(X, y)

SVC(C=inf, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape=None, degree=3, gamma='auto', kernel='linear',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)

# Bad models

import numpy as np

x0 = np.linspace(0, 5.5, 200)
pred_1 = 5*x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 * x0 + 0.5

def plot_svc_decision_boundary(svm_clf, xmin, xmax):
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]

    # At the decision boundary, w0*x0 + w1*x1 + b = 0
    # => x1 = -w0/w1 * x0 - b/w1
    x0 = np.linspace(xmin, xmax, 200)
    decision_boundary = -w[0]/w[1] * x0 - b/w[1]

    margin = 1/w[1]
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin

    svs = svm_clf.support_vectors_
    plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
    plt.plot(x0, decision_boundary, "k-",  linewidth=2)
    plt.plot(x0, gutter_up,         "k--", linewidth=2)
    plt.plot(x0, gutter_down,       "k--", linewidth=2)

plt.figure(figsize=(12,2.7))

plt.subplot(121)
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "m-", linewidth=2)
plt.plot(x0, pred_3, "r-", linewidth=2)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 5.5, 0, 2])

plt.subplot(122)
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([0, 5.5, 0, 2])
plt.show()

# On left:
# dashed line = basically useless decision boundary.
# solid lines = OK for this dataset, but no margins. Probably will not work well on new instances.

# On right: SVM finds widest possible "street" between classes.

# sensitivity to feature scaling:

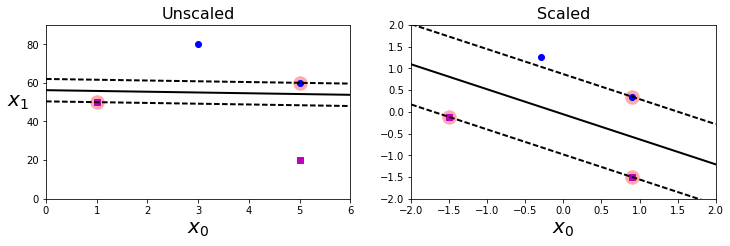
Xs = np.array([[1, 50], [5, 20], [3, 80], [5, 60]]).astype(np.float64)
ys = np.array([0, 0, 1, 1])
svm_clf = SVC(kernel="linear", C=100)
svm_clf.fit(Xs, ys)

plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(Xs[:, 0][ys==1], Xs[:, 1][ys==1], "bo")
plt.plot(Xs[:, 0][ys==0], Xs[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, 0, 6)
plt.xlabel("$x_0$", fontsize=20)
plt.ylabel("$x_1$  ", fontsize=20, rotation=0)
plt.title("Unscaled", fontsize=16)
plt.axis([0, 6, 0, 90])

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(Xs)
svm_clf.fit(X_scaled, ys)

plt.subplot(122)
plt.plot(X_scaled[:, 0][ys==1], X_scaled[:, 1][ys==1], "bo")
plt.plot(X_scaled[:, 0][ys==0], X_scaled[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, -2, 2)
plt.xlabel("$x_0$", fontsize=20)
plt.title("Scaled", fontsize=16)
plt.axis([-2, 2, -2, 2])

# SVMs are sensitive to feature scaling. 
# Plot on right has much more robust feature boundary.

[-2, 2, -2, 2]

X_scaled

array([[-1.50755672, -0.11547005],
       [ 0.90453403, -1.5011107 ],
       [-0.30151134,  1.27017059],
       [ 0.90453403,  0.34641016]])

# "hard" margin classification:
# - all instances need to be "out of the street".
# - all instances need to be "on the right side of the street".
# problem: doable only if data is linearly separable
# problem: very sensitive to outliers

X_outliers = np.array([[3.4, 1.3], [3.2, 0.8]])
y_outliers = np.array([0, 0])
Xo1 = np.concatenate([X, X_outliers[:1]], axis=0)
yo1 = np.concatenate([y, y_outliers[:1]], axis=0)
Xo2 = np.concatenate([X, X_outliers[1:]], axis=0)
yo2 = np.concatenate([y, y_outliers[1:]], axis=0)

svm_clf2 = SVC(kernel="linear", C=10**9)#float("inf"))
svm_clf2.fit(Xo2, yo2)

plt.figure(figsize=(12,2.7))

plt.subplot(121)
plt.plot(Xo1[:, 0][yo1==1], Xo1[:, 1][yo1==1], "bs")
plt.plot(Xo1[:, 0][yo1==0], Xo1[:, 1][yo1==0], "yo")
plt.text(0.3, 1.0, "Impossible!", fontsize=20, color="red")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.annotate("Outlier",
             xy=(X_outliers[0][0], X_outliers[0][1]),
             xytext=(2.5, 1.7),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=16,
            )
plt.axis([0, 5.5, 0, 2])

plt.subplot(122)
plt.plot(Xo2[:, 0][yo2==1], Xo2[:, 1][yo2==1], "bs")
plt.plot(Xo2[:, 0][yo2==0], Xo2[:, 1][yo2==0], "yo")
plot_svc_decision_boundary(svm_clf2, 0, 5.5)
plt.xlabel("Petal length", fontsize=14)
plt.annotate("Outlier",
             xy=(X_outliers[1][0], X_outliers[1][1]),
             xytext=(3.2, 0.08),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=16,
            )
plt.axis([0, 5.5, 0, 2])

[0, 5.5, 0, 2]

X_scaled

array([[-1.50755672, -0.11547005],
       [ 0.90453403, -1.5011107 ],
       [-0.30151134,  1.27017059],
       [ 0.90453403,  0.34641016]])

# soluton to "hard margins" problem:
# control hardness with C hyperparameter

from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.float64)  # Iris-Virginica

scaler = StandardScaler()
svm_clf1 = LinearSVC(C=100, loss="hinge")
svm_clf2 = LinearSVC(C=1, loss="hinge")

scaled_svm_clf1 = Pipeline((
        ("scaler", scaler),
        ("linear_svc", svm_clf1),
    ))
scaled_svm_clf2 = Pipeline((
        ("scaler", scaler),
        ("linear_svc", svm_clf2),
    ))

scaled_svm_clf1.fit(X, y)
scaled_svm_clf2.fit(X, y)

scaled_svm_clf2.predict([[5.5, 1.7]])

array([ 1.])

X_scaled

array([[-1.50755672, -0.11547005],
       [ 0.90453403, -1.5011107 ],
       [-0.30151134,  1.27017059],
       [ 0.90453403,  0.34641016]])

# Convert to unscaled parameters
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])

# Find support vectors (LinearSVC does not do this automatically)
t = y * 2 - 1
support_vectors_idx1 = (t * (X.dot(w1) + b1) < 1).ravel()
support_vectors_idx2 = (t * (X.dot(w2) + b2) < 1).ravel()
svm_clf1.support_vectors_ = X[support_vectors_idx1]
svm_clf2.support_vectors_ = X[support_vectors_idx2]

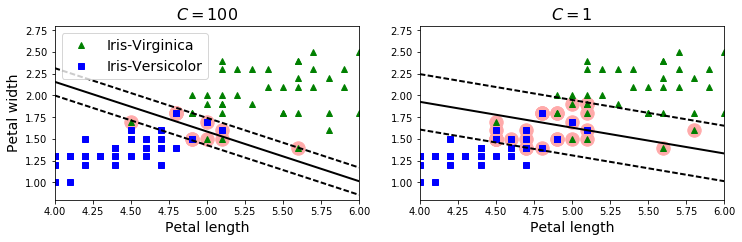
plt.figure(figsize=(12,3.2))
plt.subplot(121)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris-Virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris-Versicolor")
plot_svc_decision_boundary(svm_clf1, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])

plt.subplot(122)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 6)
plt.xlabel("Petal length", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([4, 6, 0.8, 2.8])

[4, 6, 0.8, 2.8]

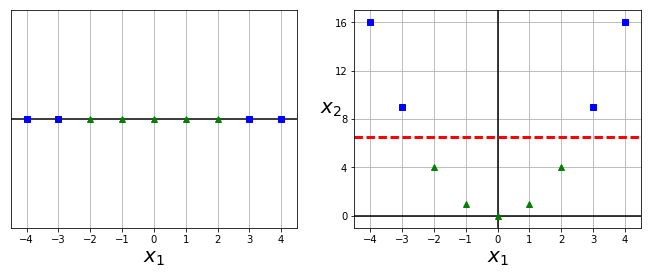
SVM Classification (Non-Linear)

# some (most?) datasets are not linearly separable. simple example below.

X1D = np.linspace(-4, 4, 9).reshape(-1, 1)

X2D = np.c_[X1D, X1D**2] # adds 2nd, non-linear dimension.

y = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])

plt.figure(figsize=(10, 4))

plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.plot(X1D[:, 0][y==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][y==1], np.zeros(5), "g^")
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r"$x_1$", fontsize=20)
plt.axis([-4.5, 4.5, -0.2, 0.2])

plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(X2D[:, 0][y==0], X2D[:, 1][y==0], "bs")
plt.plot(X2D[:, 0][y==1], X2D[:, 1][y==1], "g^")
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plt.gca().get_yaxis().set_ticks([0, 4, 8, 12, 16])
plt.plot([-4.5, 4.5], [6.5, 6.5], "r--", linewidth=3)
plt.axis([-4.5, 4.5, -1, 17])

plt.subplots_adjust(right=1)

#save_fig("higher_dimensions_plot", tight_layout=False)
plt.show()

# result: adding 2nd dimension (on right) makes dataset linearly separable

# test on "moons" dataset

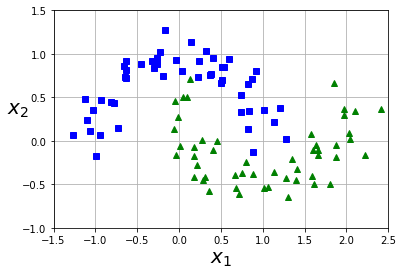
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)

def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)

plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

# do this in Scikit with a Pipeline. Contents:
# 1) Polynomial Features
# 2) StandardScaler
# 3) LinearSVC

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

polynomial_svm_clf = Pipeline((
        ("poly_features", PolynomialFeatures(degree=3)),
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge"))
    ))

polynomial_svm_clf.fit(X, y)

def plot_predictions(clf, axes):
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)
    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)

plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])

#save_fig("moons_polynomial_svc_plot")
plt.show()

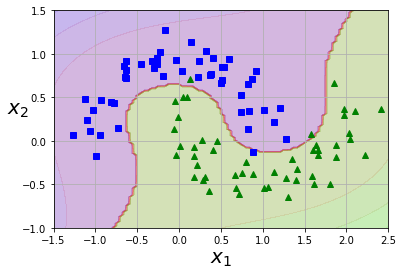
Solving polynomial-feature problems (aka combinatorial explosion) via the kernel trick

from sklearn.svm import SVC

# train SVM classifier using 3rd-degree polynomial kernel
poly_kernel_svm_clf = Pipeline((
    ("scaler", StandardScaler()),
    ("svm_clf", SVC(
        kernel="poly", degree=3, coef0=1, C=5))))

# train SVM classifier using 10th-degree polynomial kernel (for comparison)
poly100_kernel_svm_clf = Pipeline((
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
    ))

poly_kernel_svm_clf.fit(X, y)
poly100_kernel_svm_clf.fit(X, y)

plt.figure(figsize=(11, 4))

plt.subplot(121)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)

plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)

#save_fig("moons_kernelized_polynomial_svc_plot")
plt.show()

# left: 3rd-degree polynomial; right: 10th-degree polynomial.
# if overfitting, reduce polynomial degree. if underfitting, bump it up.
# "coef0": controls high- vs low-degree polynomial influence.

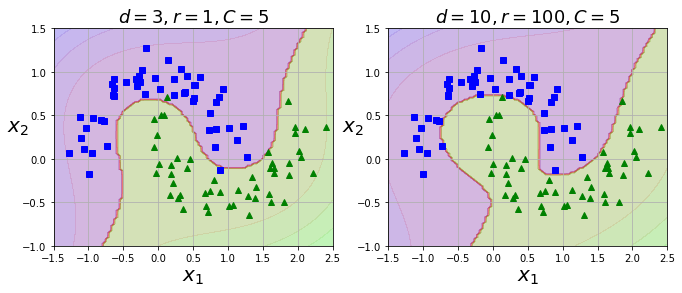
Adding Similarity Features

similarity function: measures how much an instance resembles specified landmark.

# define similarity function to be Gaussian Radial Basis Function (RBF)
# equals 0 (far away) to 1 (at landmark)

def gaussian_rbf(x, landmark, gamma):
    return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1)**2)

gamma = 0.3

x1s = np.linspace(-4.5, 4.5, 200).reshape(-1, 1)
x2s = gaussian_rbf(x1s, -2, gamma)
x3s = gaussian_rbf(x1s, 1, gamma)

XK = np.c_[gaussian_rbf(X1D, -2, gamma), gaussian_rbf(X1D, 1, gamma)]
yk = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])

plt.figure(figsize=(11, 4))

plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.scatter(x=[-2, 1], y=[0, 0], s=150, alpha=0.5, c="red")
plt.plot(X1D[:, 0][yk==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][yk==1], np.zeros(5), "g^")
plt.plot(x1s, x2s, "g--")
plt.plot(x1s, x3s, "b:")
plt.gca().get_yaxis().set_ticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"Similarity", fontsize=14)
plt.annotate(r'$\mathbf{x}$',
             xy=(X1D[3, 0], 0),
             xytext=(-0.5, 0.20),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=18,
            )
plt.text(-2, 0.9, "$x_2$", ha="center", fontsize=20)
plt.text(1, 0.9, "$x_3$", ha="center", fontsize=20)
plt.axis([-4.5, 4.5, -0.1, 1.1])

plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(XK[:, 0][yk==0], XK[:, 1][yk==0], "bs")
plt.plot(XK[:, 0][yk==1], XK[:, 1][yk==1], "g^")
plt.xlabel(r"$x_2$", fontsize=20)
plt.ylabel(r"$x_3$  ", fontsize=20, rotation=0)
plt.annotate(r'$\phi\left(\mathbf{x}\right)$',
             xy=(XK[3, 0], XK[3, 1]),
             xytext=(0.65, 0.50),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=18,
            )
plt.plot([-0.1, 1.1], [0.57, -0.1], "r--", linewidth=3)
plt.axis([-0.1, 1.1, -0.1, 1.1])

plt.subplots_adjust(right=1)

#save_fig("kernel_method_plot")
plt.show()

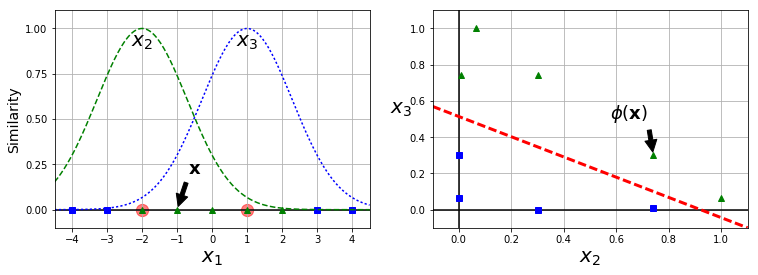
x1_example = X1D[3, 0]
for landmark in (-2, 1):
    k = gaussian_rbf(np.array([[x1_example]]), np.array([[landmark]]), gamma)
    print("Phi({}, {}) = {}".format(x1_example, landmark, k))

Phi(-1.0, -2) = [ 0.74081822]
Phi(-1.0, 1) = [ 0.30119421]

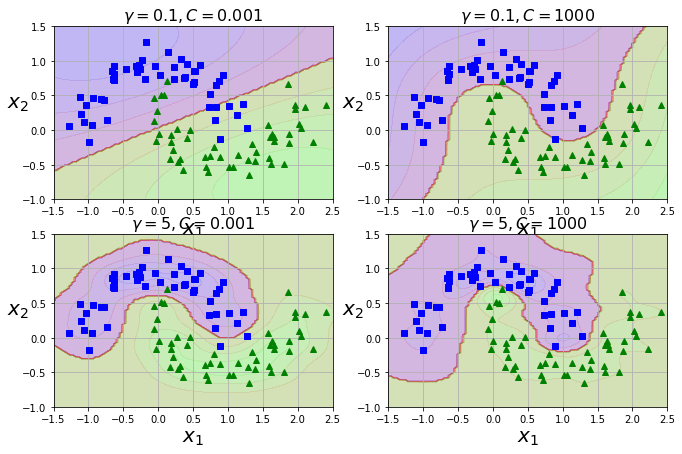
Using a Gaussian RBF Kernel

rbf_kernel_svm_clf = Pipeline((
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
    ))
rbf_kernel_svm_clf.fit(X, y)

from sklearn.svm import SVC

gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)

svm_clfs = []
for gamma, C in hyperparams:
    rbf_kernel_svm_clf = Pipeline((
            ("scaler", StandardScaler()),
            ("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
        ))
    rbf_kernel_svm_clf.fit(X, y)
    svm_clfs.append(rbf_kernel_svm_clf)

plt.figure(figsize=(11, 7))

for i, svm_clf in enumerate(svm_clfs):
    plt.subplot(221 + i)
    plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
    plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
    gamma, C = hyperparams[i]
    plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)

#save_fig("moons_rbf_svc_plot")
plt.show()

# below: model trained with different values of gamma and C.
# GAMMA:
# bigger gamma = narrower bell curve, so each instance's area of influence = smaller.
# smaller gamma: bigger bell curve = smoother decision boundary.

Computational Complexity

LinearSVC class: based on liblinear library. Doesn't support kernel trick. Scales linearly to #instances and #features; training complexity ~O(mxn).
SVC class: based on libsvm library. Does support kernel trick. Training complexity is O(m^2xn) to O(m^3xn) = MUCH slower on larger training datasets.

SVM Regression (Linear & Non-Linear)

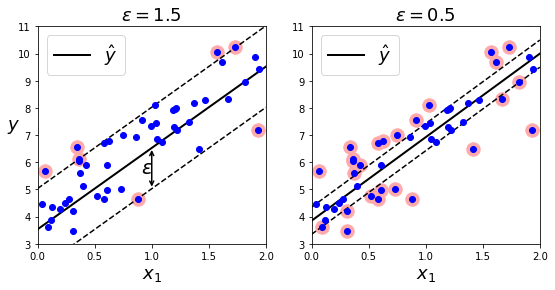
Objectives: 1) fit max #instances on the street; 2) find min #margin violations (instances "off" the street").
Width controlled by epsilon hyperparameter.
Below: random linear dataset. two training results with different vals of epsilon.

from sklearn.svm import LinearSVR
import numpy.random as rnd

rnd.seed(42)
m = 50
X = 2 * rnd.rand(m, 1)
y = (4 + 3 * X + rnd.randn(m, 1)).ravel()

svm_reg1 = LinearSVR(epsilon=1.5)
svm_reg2 = LinearSVR(epsilon=0.5)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)

def find_support_vectors(svm_reg, X, y):
    y_pred = svm_reg.predict(X)
    off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
    return np.argwhere(off_margin)

svm_reg1.support_ = find_support_vectors(svm_reg1, X, y)
svm_reg2.support_ = find_support_vectors(svm_reg2, X, y)

eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])

def plot_svm_regression(svm_reg, X, y, axes):
    x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
    y_pred = svm_reg.predict(x1s)
    plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
    plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
    plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
    plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
    plt.plot(X, y, "bo")
    plt.xlabel(r"$x_1$", fontsize=18)
    plt.legend(loc="upper left", fontsize=18)
    plt.axis(axes)

plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_reg1, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
#plt.plot([eps_x1, eps_x1], [eps_y_pred, eps_y_pred - svm_reg1.epsilon], "k-", linewidth=2)
plt.annotate(
        '', xy=(eps_x1, eps_y_pred), xycoords='data',
        xytext=(eps_x1, eps_y_pred - svm_reg1.epsilon),
        textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
    )
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.subplot(122)
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)
#save_fig("svm_regression_plot")
plt.show()

# Use kernel-ized SVM model to handle nonlinear regression jobs.

from sklearn.svm import SVR

# random quadratic training set.
rnd.seed(42)
m = 100
X = 2 * rnd.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + rnd.randn(m, 1)/10).ravel()

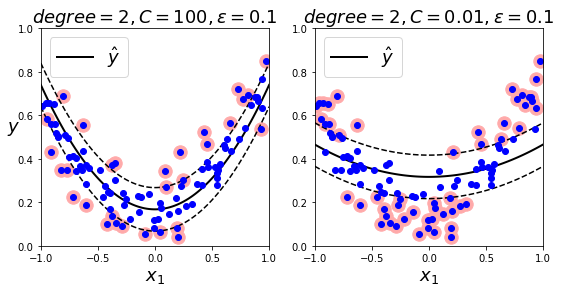
svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1)
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1)
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)

SVR(C=0.01, cache_size=200, coef0=0.0, degree=2, epsilon=0.1, gamma='auto',
  kernel='poly', max_iter=-1, shrinking=True, tol=0.001, verbose=False)

plt.figure(figsize=(9, 4))
plt.subplot(121)
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.subplot(122)
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)
#save_fig("svm_with_polynomial_kernel_plot")
plt.show()

# left: little regularization (large C)
# right: much more regularization (little C)

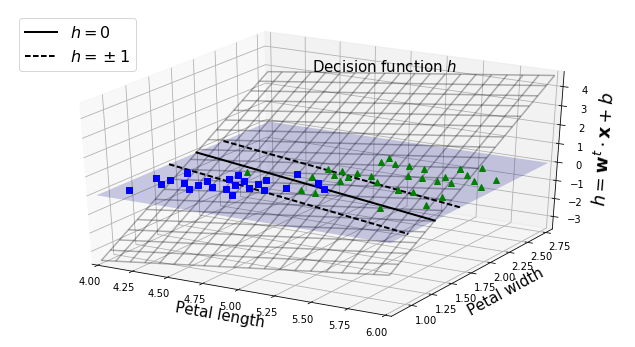
Under the Hood

conventions: b = bias term; w = feature weights vector.

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]  # petal length, petal width
y = (iris["target"] == 2).astype(np.float64)  # Iris-Virginica

from mpl_toolkits.mplot3d import Axes3D

def plot_3D_decision_function(ax, w, b, x1_lim=[4, 6], x2_lim=[0.8, 2.8]):
    x1_in_bounds = (X[:, 0] > x1_lim[0]) & (X[:, 0] < x1_lim[1])
    X_crop = X[x1_in_bounds]
    y_crop = y[x1_in_bounds]
    x1s = np.linspace(x1_lim[0], x1_lim[1], 20)
    x2s = np.linspace(x2_lim[0], x2_lim[1], 20)
    x1, x2 = np.meshgrid(x1s, x2s)
    xs = np.c_[x1.ravel(), x2.ravel()]
    df = (xs.dot(w) + b).reshape(x1.shape)
    m = 1 / np.linalg.norm(w)
    boundary_x2s = -x1s*(w[0]/w[1])-b/w[1]
    margin_x2s_1 = -x1s*(w[0]/w[1])-(b-1)/w[1]
    margin_x2s_2 = -x1s*(w[0]/w[1])-(b+1)/w[1]
    ax.plot_surface(x1s, x2, 0, color="b", alpha=0.2, cstride=100, rstride=100)
    ax.plot(x1s, boundary_x2s, 0, "k-", linewidth=2, label=r"$h=0$")
    ax.plot(x1s, margin_x2s_1, 0, "k--", linewidth=2, label=r"$h=\pm 1$")
    ax.plot(x1s, margin_x2s_2, 0, "k--", linewidth=2)
    ax.plot(X_crop[:, 0][y_crop==1], X_crop[:, 1][y_crop==1], 0, "g^")
    ax.plot_wireframe(x1, x2, df, alpha=0.3, color="k")
    ax.plot(X_crop[:, 0][y_crop==0], X_crop[:, 1][y_crop==0], 0, "bs")
    ax.axis(x1_lim + x2_lim)
    ax.text(4.5, 2.5, 3.8, "Decision function $h$", fontsize=15)
    ax.set_xlabel(r"Petal length", fontsize=15)
    ax.set_ylabel(r"Petal width", fontsize=15)
    ax.set_zlabel(r"$h = \mathbf{w}^t \cdot \mathbf{x} + b$", fontsize=18)
    ax.legend(loc="upper left", fontsize=16)

fig = plt.figure(figsize=(11, 6))
ax1 = fig.add_subplot(111, projection='3d')
plot_3D_decision_function(ax1, w=svm_clf2.coef_[0], b=svm_clf2.intercept_[0])

#save_fig("iris_3D_plot")
plt.show()

Training Objectives

Slope of a decision function equals a weight vector's norm (||w||)
Divide slope by 2 ==> any points where decision function = +1/-1 will be 2x away from decision boundary.
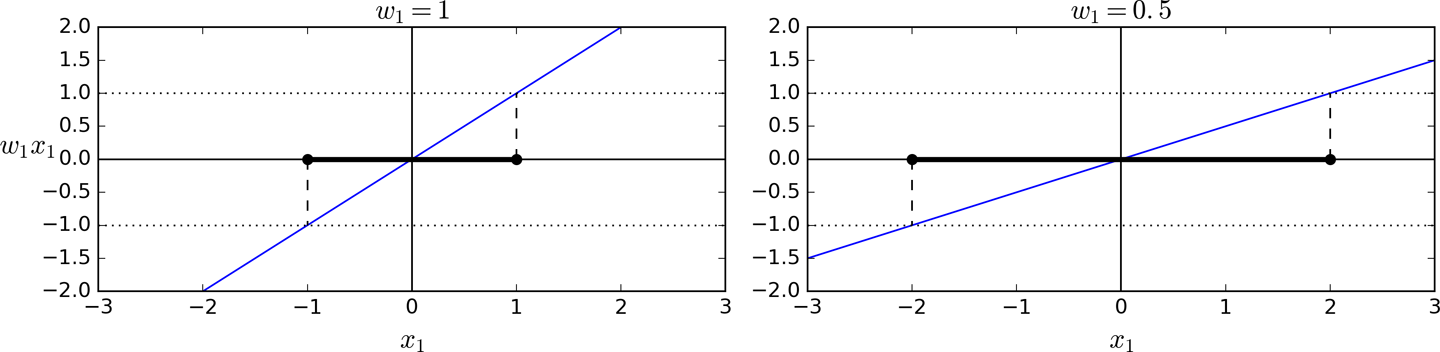
So we want minimal ||w|| to get max margins
If we also want zero margin violations, then decision function needs to be GT1 (positive) and LT1 (negative).
if soft margins OK - need to define a slack variable (C) for tradeoff.

Quadratic programming

Hard- & soft-margin problems = convex quadratic optimization problems with linear constraints, ie quadratic programming (QP) problems. See Convex Optimization for more info.

todo: The dual problem

todo: Kernelized SVM

todo: Online (incremental learning) SVMs

Linear SVM classifiers often use SGD to find a min-cost solution. SGD converges much more slowly than QP-based methods.
implementation:
implementation:

ch05 support vector machines.md

SVM Classification (Linear)

SVM Classification (Non-Linear)

Solving polynomial-feature problems (aka combinatorial explosion) via the kernel trick

Adding Similarity Features

Using a Gaussian RBF Kernel

Computational Complexity

SVM Regression (Linear & Non-Linear)

Under the Hood

Training Objectives

Quadratic programming

todo: The dual problem

todo: Kernelized SVM

todo: Online (incremental learning) SVMs

results matching ""

No results matching ""