Intro
import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt
Voting Classifiers
- Good classifiers can be built by aggregating predictions of various weaker classifiers, and returning the class that gets the most votes. (A "hard voting" classifier.)
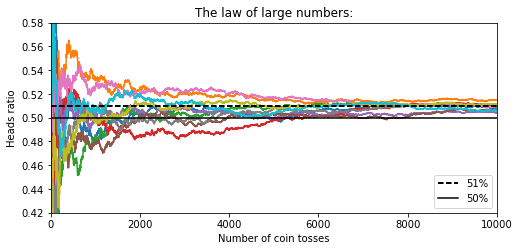
heads_proba = 0.51
coin_tosses = (rnd.rand(10000, 10) < heads_proba).astype(np.int32)
cumulative_heads_ratio = np.cumsum(
coin_tosses, axis=0) / np.arange(1, 10001).reshape(-1, 1)
#cumulative_heads_ratio
plt.figure(figsize=(8,3.5))
plt.plot(cumulative_heads_ratio)
plt.plot([0, 10000], [0.51, 0.51], "k--", linewidth=2, label="51%")
plt.plot([0, 10000], [0.5, 0.5], "k-", label="50%")
plt.xlabel("Number of coin tosses")
plt.ylabel("Heads ratio")
plt.legend(loc="lower right")
plt.title("The law of large numbers:")
plt.axis([0, 10000, 0.42, 0.58])
#save_fig("law_of_large_numbers_plot")
plt.show()
# build a voting classifier in Scikit using three weaker classifiers
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_moons
# use moons dataset
X, y = make_moons(
n_samples=500,
noise=0.30,
random_state=42)
X_train, X_test, y_train, y_test = train_test_split(
X, y, random_state=42)
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
log_clf = LogisticRegression(random_state=42)
rnd_clf = RandomForestClassifier(random_state=42)
svm_clf = SVC(probability=True, random_state=42)
# voting classifier = logistic + random forest + SVC
voting_clf = VotingClassifier(
estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
voting='soft'
)
voting_clf.fit(X_train, y_train)
# let's see how each individual classifier did:
from sklearn.metrics import accuracy_score
for clf in (log_clf, rnd_clf, svm_clf, voting_clf):
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(clf.__class__.__name__, accuracy_score(y_test, y_pred))
# voting classifier did better than 3 individual ones!
LogisticRegression 0.864
RandomForestClassifier 0.872
SVC 0.888
VotingClassifier 0.912
If all classifiers can estimate class probabilities (they have a predict_proba() method), use Scikit to predict highest class probability, averaged over all individual classifiers. (soft voting)
Often better than hard voting because it gives more weight to highly confident votes. Replace voting="hard" with "soft" & ensure all classifiers can estimate class probabilities. (SVC cannot by default -set probability param to True.)
This tells SVC to use cross-validation to estimate class probabilities. Slows training times & adds a predict_proba() method).
Bagging & Pasting
- Another approach: use same training algorithm, but apply it to different subsets of the training dataset.
- bagging: sampling the dataset with replacement.
- pasting: sampling the dataset without replacement.
- Final prediction = based on an aggregation function.
- Predictions can be made in parallel -- good scaling properties.
from sklearn.datasets import make_moons
from sklearn.ensemble import BaggingClassifier
from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier
# Train ensemble of 500 Decision Tree classifiers
# each using 100 training instances - randomly sampled from training set
# with replacement.
bag_clf = BaggingClassifier(
DecisionTreeClassifier(random_state=42),
n_estimators=500,
max_samples=100,
bootstrap=True, # set to False for pasting instead of bagging.
n_jobs=-1,
random_state=42)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
print(accuracy_score(y_test, y_pred))
0.904
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)
y_pred_tree = tree_clf.predict(X_test)
print(accuracy_score(y_test, y_pred_tree))
0.856
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf, X, y, axes=[-1.5, 2.5, -1, 1.5], alpha=0.5, contour=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap, linewidth=10)
if contour:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", alpha=alpha)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", alpha=alpha)
plt.axis(axes)
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
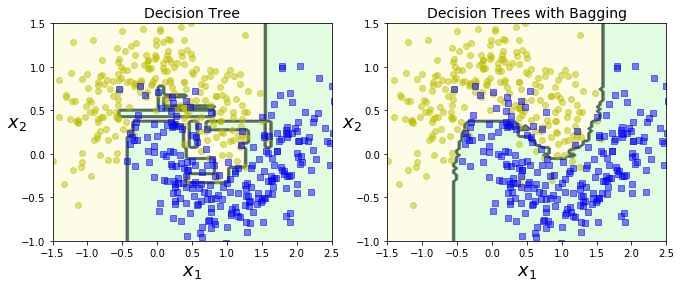
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_decision_boundary(tree_clf, X, y)
plt.title("Decision Tree", fontsize=14)
plt.subplot(122)
plot_decision_boundary(bag_clf, X, y)
plt.title("Decision Trees with Bagging", fontsize=14)
#save_fig("decision_tree_without_and_with_bagging_plot")
plt.show()
Out of Bag Evaluation
- Bagging: some instances may be sampled multiple times - others not at all. On avg, ~63% of training samples are used. Remainder 37% = "out of bag".
- use oob_score=True in Scikit to do automatic oob evaluation after training.
# oob_score_: predicts classifier results on test set.
bag_clf = BaggingClassifier(
DecisionTreeClassifier(),
n_estimators=500,
bootstrap=True,
n_jobs=-1,
oob_score=True
)
bag_clf.fit(X_train, y_train)
bag_clf.oob_score_
0.89866666666666661
# did oob_score_ do a good job?
from sklearn.metrics import accuracy_score
y_pred = bag_clf.predict(X_test)
accuracy_score(y_test,y_pred)
0.90400000000000003
# oob decision functionfor each training instance
bag_clf.oob_decision_function_
array([[ 0.36363636, 0.63636364],
[ 0.38586957, 0.61413043],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.06632653, 0.93367347],
[ 0.30769231, 0.69230769],
[ 0.03015075, 0.96984925],
[ 0.99444444, 0.00555556],
[ 0.94708995, 0.05291005],
[ 0.79 , 0.21 ],
[ 0.00507614, 0.99492386],
[ 0.77456647, 0.22543353],
[ 0.84269663, 0.15730337],
[ 0.95480226, 0.04519774],
[ 0.06557377, 0.93442623],
[ 0. , 1. ],
[ 0.98 , 0.02 ],
[ 0.95505618, 0.04494382],
[ 1. , 0. ],
[ 0.01086957, 0.98913043],
[ 0.3372093 , 0.6627907 ],
[ 0.89949749, 0.10050251],
[ 1. , 0. ],
[ 0.96666667, 0.03333333],
[ 0. , 1. ],
[ 0.99375 , 0.00625 ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.64285714, 0.35714286],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.14444444, 0.85555556],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.33152174, 0.66847826],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.22702703, 0.77297297],
[ 0.41212121, 0.58787879],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0.02777778, 0.97222222],
[ 1. , 0. ],
[ 0.00561798, 0.99438202],
[ 0.99418605, 0.00581395],
[ 0.89265537, 0.10734463],
[ 0.96273292, 0.03726708],
[ 0.9494382 , 0.0505618 ],
[ 0. , 1. ],
[ 0.03846154, 0.96153846],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.00540541, 0.99459459],
[ 1. , 0. ],
[ 0.81182796, 0.18817204],
[ 0.44776119, 0.55223881],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.63387978, 0.36612022],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0.845 , 0.155 ],
[ 1. , 0. ],
[ 0.55 , 0.45 ],
[ 0.13372093, 0.86627907],
[ 0.68390805, 0.31609195],
[ 0.87700535, 0.12299465],
[ 0. , 1. ],
[ 0.19487179, 0.80512821],
[ 0.88324873, 0.11675127],
[ 1. , 0. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.07017544, 0.92982456],
[ 0.0326087 , 0.9673913 ],
[ 0.29120879, 0.70879121],
[ 1. , 0. ],
[ 0.00487805, 0.99512195],
[ 0.87700535, 0.12299465],
[ 0.00543478, 0.99456522],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.26395939, 0.73604061],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.92227979, 0.07772021],
[ 0.78494624, 0.21505376],
[ 0.005 , 0.995 ],
[ 1. , 0. ],
[ 0.1957672 , 0.8042328 ],
[ 0.6631016 , 0.3368984 ],
[ 0. , 1. ],
[ 0.03529412, 0.96470588],
[ 0.4974359 , 0.5025641 ],
[ 1. , 0. ],
[ 0.01785714, 0.98214286],
[ 0.99465241, 0.00534759],
[ 0.23626374, 0.76373626],
[ 0.5270936 , 0.4729064 ],
[ 1. , 0. ],
[ 0.01694915, 0.98305085],
[ 0.99568966, 0.00431034],
[ 0.25988701, 0.74011299],
[ 0.92982456, 0.07017544],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.80748663, 0.19251337],
[ 1. , 0. ],
[ 0.02105263, 0.97894737],
[ 1. , 0. ],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0.98477157, 0.01522843],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.92655367, 0.07344633],
[ 1. , 0. ],
[ 0.01485149, 0.98514851],
[ 0.29145729, 0.70854271],
[ 0.96216216, 0.03783784],
[ 0.29608939, 0.70391061],
[ 0.9893617 , 0.0106383 ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.73913043, 0.26086957],
[ 0.40251572, 0.59748428],
[ 0.46031746, 0.53968254],
[ 0.88297872, 0.11702128],
[ 0.92090395, 0.07909605],
[ 0.06818182, 0.93181818],
[ 0.82634731, 0.17365269],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.01169591, 0.98830409],
[ 1. , 0. ],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0.00529101, 0.99470899],
[ 0. , 1. ],
[ 0.00540541, 0.99459459],
[ 0. , 1. ],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0.95238095, 0.04761905],
[ 1. , 0. ],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.34065934, 0.65934066],
[ 0.23529412, 0.76470588],
[ 0.00534759, 0.99465241],
[ 0.00512821, 0.99487179],
[ 0.31213873, 0.68786127],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.00613497, 0.99386503],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.00578035, 0.99421965],
[ 0.63313609, 0.36686391],
[ 0.9027027 , 0.0972973 ],
[ 0. , 1. ],
[ 0.98963731, 0.01036269],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.07978723, 0.92021277],
[ 1. , 0. ],
[ 0.03645833, 0.96354167],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.01818182, 0.98181818],
[ 1. , 0. ],
[ 0.96276596, 0.03723404],
[ 0.77173913, 0.22826087],
[ 0.65536723, 0.34463277],
[ 0. , 1. ],
[ 0.14832536, 0.85167464],
[ 1. , 0. ],
[ 0.96296296, 0.03703704],
[ 0.97849462, 0.02150538],
[ 1. , 0. ],
[ 0.00564972, 0.99435028],
[ 0. , 1. ],
[ 0.48924731, 0.51075269],
[ 0.86243386, 0.13756614],
[ 0. , 1. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.00543478, 0.99456522],
[ 0. , 1. ],
[ 0.96208531, 0.03791469],
[ 0. , 1. ],
[ 0.21590909, 0.78409091],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.96875 , 0.03125 ],
[ 0.8021978 , 0.1978022 ],
[ 1. , 0. ],
[ 0.00568182, 0.99431818],
[ 0.05670103, 0.94329897],
[ 1. , 0. ],
[ 0.01898734, 0.98101266],
[ 0. , 1. ],
[ 0.08888889, 0.91111111],
[ 1. , 0. ],
[ 0.77439024, 0.22560976],
[ 0. , 1. ],
[ 0.86666667, 0.13333333],
[ 0.99441341, 0.00558659],
[ 0.14634146, 0.85365854],
[ 0.19487179, 0.80512821],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.26111111, 0.73888889],
[ 0.96391753, 0.03608247],
[ 0. , 1. ],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.52147239, 0.47852761],
[ 1. , 0. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.07177033, 0.92822967],
[ 0.13333333, 0.86666667],
[ 0.99435028, 0.00564972],
[ 0.01142857, 0.98857143],
[ 1. , 0. ],
[ 0.43820225, 0.56179775],
[ 0.11290323, 0.88709677],
[ 0.5875 , 0.4125 ],
[ 0.60752688, 0.39247312],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.58125 , 0.41875 ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.18032787, 0.81967213],
[ 0.8150289 , 0.1849711 ],
[ 0.07216495, 0.92783505],
[ 1. , 0. ],
[ 0.84444444, 0.15555556],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.07772021, 0.92227979],
[ 0.02061856, 0.97938144],
[ 0. , 1. ],
[ 0.99473684, 0.00526316],
[ 0.9076087 , 0.0923913 ],
[ 0.15517241, 0.84482759],
[ 0.96174863, 0.03825137],
[ 0.00578035, 0.99421965],
[ 0.60487805, 0.39512195],
[ 0.03553299, 0.96446701],
[ 0.98958333, 0.01041667],
[ 0.82795699, 0.17204301],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.96174863, 0.03825137],
[ 0. , 1. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.32960894, 0.67039106],
[ 0.98907104, 0.01092896],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0. , 1. ],
[ 0.83240223, 0.16759777],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.79213483, 0.20786517],
[ 0.94565217, 0.05434783],
[ 1. , 0. ],
[ 0.73224044, 0.26775956],
[ 0.57142857, 0.42857143],
[ 0. , 1. ],
[ 0.91666667, 0.08333333],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.89820359, 0.10179641],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0.77272727, 0.22727273],
[ 0.14371257, 0.85628743],
[ 0.52348993, 0.47651007],
[ 0.26701571, 0.73298429],
[ 0. , 1. ],
[ 0.86486486, 0.13513514],
[ 0.83536585, 0.16463415],
[ 0.00591716, 0.99408284],
[ 1. , 0. ],
[ 0.99431818, 0.00568182],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.02659574, 0.97340426],
[ 0.96067416, 0.03932584],
[ 0.95767196, 0.04232804],
[ 1. , 0. ],
[ 0.47928994, 0.52071006],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.99459459, 0.00540541],
[ 0.03157895, 0.96842105],
[ 1. , 0. ],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 0.96601942, 0.03398058],
[ 0. , 1. ],
[ 0.04651163, 0.95348837],
[ 0. , 1. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 1. , 0. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.02040816, 0.97959184],
[ 1. , 0. ],
[ 0.13917526, 0.86082474],
[ 0. , 1. ],
[ 0.01734104, 0.98265896],
[ 0. , 1. ],
[ 0.40952381, 0.59047619],
[ 0.06818182, 0.93181818],
[ 0.23195876, 0.76804124],
[ 1. , 0. ],
[ 0.98795181, 0.01204819],
[ 0.20430108, 0.79569892],
[ 0.99438202, 0.00561798],
[ 0. , 1. ],
[ 0. , 1. ],
[ 1. , 0. ],
[ 0.97311828, 0.02688172],
[ 0.31460674, 0.68539326],
[ 0.98870056, 0.01129944],
[ 1. , 0. ],
[ 0.00581395, 0.99418605],
[ 0.99009901, 0.00990099],
[ 0. , 1. ],
[ 0.0304878 , 0.9695122 ],
[ 0.97849462, 0.02150538],
[ 1. , 0. ],
[ 0.03508772, 0.96491228],
[ 0.64864865, 0.35135135]])
Random Patches - Random Subspaces
- BaggingClassifier supports feature sampling. Params: max_features and bootstrap.
- Very useful when handling high-dimensional datasets.
- "Random patches": sampling features & sampling instances.
- "Random subspaces": sampling features & keeping all instances.
Random Forests
- RF = ensemble of Decision Trees
- Typically trained via bagging
- RandomForestClassifier: designed for DT classification
- RandomForestRegressor: designed for regression
# Train an RF classifier with 500 trees limited to 16 max nodes each.
# splitter="random": tells RF to search for best feature among
# a random subset of features.
bag_clf = BaggingClassifier(
DecisionTreeClassifier(
splitter="random",
max_leaf_nodes=16,
random_state=42),
n_estimators=500,
max_samples=1.0,
bootstrap=True,
n_jobs=-1,
random_state=42)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
from sklearn.ensemble import RandomForestClassifier
rnd_clf = RandomForestClassifier(
n_estimators=500,
max_leaf_nodes=16,
n_jobs=-1,
random_state=42)
rnd_clf.fit(X_train, y_train)
y_pred_rf = rnd_clf.predict(X_test)
# almost identical predictions
np.sum(y_pred == y_pred_rf) / len(y_pred)
0.97599999999999998
Feature importance
- important features likely to appear closer to root of tree
- unimportant features likely to appear closer to leaves - if at all.
- Scikit finds avg depth of feature appearance across all trees in an RF.
# rank features by importance in iris
# #1: petal length: 44%
from sklearn.datasets import load_iris
iris = load_iris()
rnd_clf = RandomForestClassifier(
n_estimators=500,
n_jobs=-1,
random_state=42)
rnd_clf.fit(iris["data"], iris["target"])
for name, importance in zip(
iris["feature_names"],
rnd_clf.feature_importances_):
print(name, "=", importance)
sepal length (cm) = 0.112492250999
sepal width (cm) = 0.0231192882825
petal length (cm) = 0.441030464364
petal width (cm) = 0.423357996355
rnd_clf.feature_importances_
array([ 0.11249225, 0.02311929, 0.44103046, 0.423358 ])
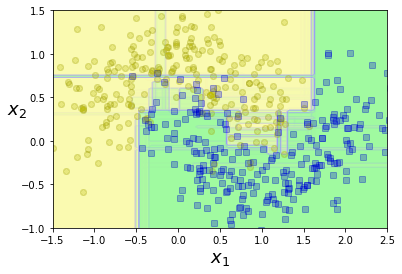
plt.figure(figsize=(6, 4))
for i in range(15):
tree_clf = DecisionTreeClassifier(
max_leaf_nodes=16,
random_state=42+i)
indices_with_replacement = rnd.randint(
0,
len(X_train),
len(X_train))
tree_clf.fit(
X[indices_with_replacement],
y[indices_with_replacement])
plot_decision_boundary(
tree_clf, X, y,
axes=[-1.5, 2.5, -1, 1.5],
alpha=0.02,
contour=False)
plt.show()
Boosting - AdaBoost
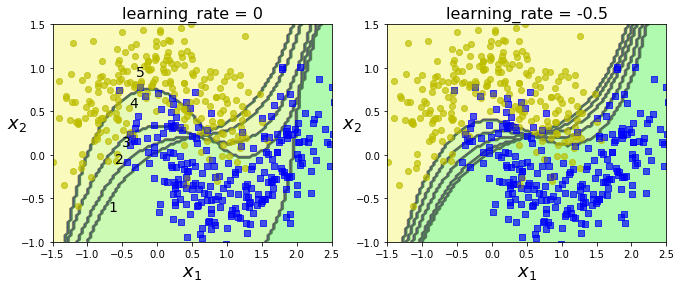
- One strategy: pay more attention to training instances that predecessor underfitted - forces new predictors to concentrate more on the "hard cases".
- Disadvantage: results depend on previous classifier (sequential), so algo cannot be parallelized. Not great for scaling.
# Plot decision boundaries of five predictors on moons dataset
m = len(X_train)
plt.figure(figsize=(11, 4))
for subplot, learning_rate in ((121, 1), (122, 0.5)):
sample_weights = np.ones(m)
for i in range(5):
plt.subplot(subplot)
svm_clf = SVC(
kernel="rbf",
C=0.05)
svm_clf.fit(
X_train, y_train,
sample_weight=sample_weights)
y_pred = svm_clf.predict(
X_train)
sample_weights[y_pred != y_train] *= (1 + learning_rate)
plot_decision_boundary(
svm_clf,
X, y,
alpha=0.2)
plt.title("learning_rate = {}".format(learning_rate - 1),
fontsize=16)
plt.subplot(121)
plt.text(-0.7, -0.65, "1", fontsize=14)
plt.text(-0.6, -0.10, "2", fontsize=14)
plt.text(-0.5, 0.10, "3", fontsize=14)
plt.text(-0.4, 0.55, "4", fontsize=14)
plt.text(-0.3, 0.90, "5", fontsize=14)
#save_fig("boosting_plot")
plt.show()
# left: 1st clf gets many wrong, so 2nd clf gets boosted values.
# right: same sequence, but learning rate cut in half.
# train AdaBoost classifier on 200 decision stumps (DS)
# DS = decision tree with max_depth=1
from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier(
DecisionTreeClassifier(max_depth=1), n_estimators=200,
algorithm="SAMME.R", learning_rate=0.5, random_state=42
)
ada_clf.fit(X_train, y_train)
plot_decision_boundary(ada_clf, X, y)
plt.show()
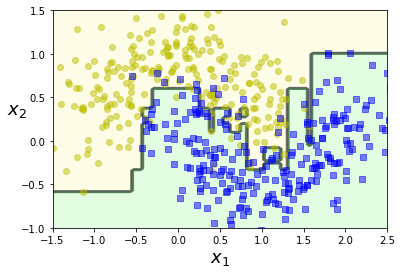
Boosting - Gradient Boosting
- Similar to AdaBoost (continually correcting the predecessors in an ensemble. Instead of tweaking instance weights on each iteration, GB fits the predictor to the residual errors of the previous predictor.
from sklearn.tree import DecisionTreeRegressor
# training set: a noisy quadratic function
rnd.seed(42)
X = rnd.rand(100, 1) - 0.5
y = 3*X[:, 0]**2 + 0.05 * rnd.randn(100)
# train Regressor
tree_reg1 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg1.fit(X, y)
# now train 2nd Regressor using errors made by 1st one.
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg2.fit(X, y2)
# now train 3rd Regressor using errors made by 2nd one.
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg3.fit(X, y3)
X_new = np.array([[0.8]])
# now have ensemble w/ three trees.
y_pred = sum(tree.predict(X_new) for tree in (
tree_reg1, tree_reg2, tree_reg3))
print(y_pred)
[ 0.75026781]
def plot_predictions(
regressors, X, y, axes,
label=None,
style="r-",
data_style="b.",
data_label=None):
x1 = np.linspace(axes[0], axes[1], 500)
y_pred = sum(
regressor.predict(x1.reshape(-1, 1)) for regressor in regressors)
plt.plot(X[:, 0], y, data_style, label=data_label)
plt.plot(x1, y_pred, style, linewidth=2, label=label)
if label or data_label:
plt.legend(loc="upper center", fontsize=16)
plt.axis(axes)
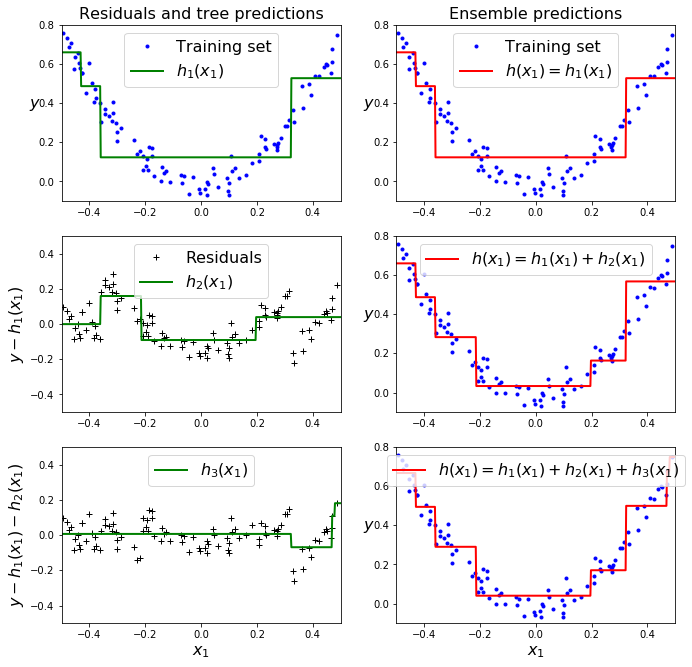
plt.figure(figsize=(11,11))
plt.subplot(321)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h_1(x_1)$", style="g-", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Residuals and tree predictions", fontsize=16)
plt.subplot(322)
plot_predictions([tree_reg1], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1)$", data_label="Training set")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.title("Ensemble predictions", fontsize=16)
plt.subplot(323)
plot_predictions([tree_reg2], X, y2, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_2(x_1)$", style="g-", data_style="k+", data_label="Residuals")
plt.ylabel("$y - h_1(x_1)$", fontsize=16)
plt.subplot(324)
plot_predictions([tree_reg1, tree_reg2], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1)$")
plt.ylabel("$y$", fontsize=16, rotation=0)
plt.subplot(325)
plot_predictions([tree_reg3], X, y3, axes=[-0.5, 0.5, -0.5, 0.5], label="$h_3(x_1)$", style="g-", data_style="k+")
plt.ylabel("$y - h_1(x_1) - h_2(x_1)$", fontsize=16)
plt.xlabel("$x_1$", fontsize=16)
plt.subplot(326)
plot_predictions([tree_reg1, tree_reg2, tree_reg3], X, y, axes=[-0.5, 0.5, -0.1, 0.8], label="$h(x_1) = h_1(x_1) + h_2(x_1) + h_3(x_1)$")
plt.xlabel("$x_1$", fontsize=16)
plt.ylabel("$y$", fontsize=16, rotation=0)
#save_fig("gradient_boosting_plot")
plt.show()
# 1st row: ensemble = only one tree: predictions match 1st tree.
# 2nd row: new tree trained on residual errors of 1st tree.
# 3rd row: " "
# result: ensemble predictions get better as trees are added.
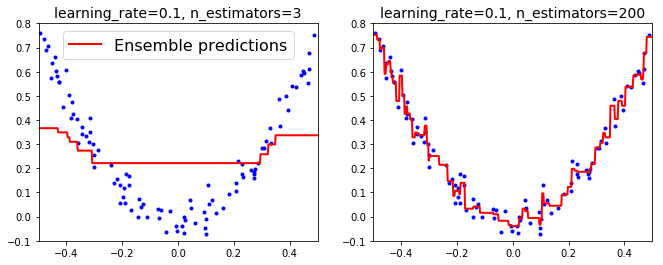
- learning_rate param controls contribution of each tree. Low values (ex: 0.1) = need more trees in ensemble to fit training set, but predictions usually generalize better. (This is called shrinkage.)
# two GBRT ensembles trained with low learning rate
from sklearn.ensemble import GradientBoostingRegressor
gbrt = GradientBoostingRegressor(
max_depth=2,
n_estimators=3,
learning_rate=0.1,
random_state=42)
gbrt.fit(X, y)
gbrt_slow = GradientBoostingRegressor(
max_depth=2,
n_estimators=200,
learning_rate=0.1,
random_state=42)
gbrt_slow.fit(X, y)
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_predictions(
[gbrt], X, y,
axes=[-0.5, 0.5, -0.1, 0.8],
label="Ensemble predictions")
plt.title("learning_rate={}, n_estimators={}".format(gbrt.learning_rate, gbrt.n_estimators), fontsize=14)
plt.subplot(122)
plot_predictions(
[gbrt_slow], X, y,
axes=[-0.5, 0.5, -0.1, 0.8])
plt.title("learning_rate={}, n_estimators={}".format(gbrt_slow.learning_rate, gbrt_slow.n_estimators), fontsize=14)
#save_fig("gbrt_learning_rate_plot")
plt.show()
# left: not enough trees (underfits)
# right: too many trees (overfits)
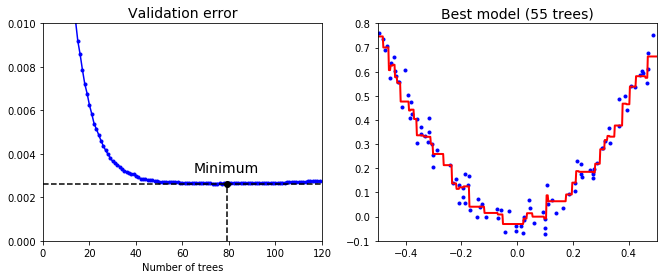
- To find optimal number of trees - use early stopping method.
- staged_predict method: returns iterator
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
X_train, X_val, y_train, y_val = train_test_split(X, y)
# train GRBR regressor with 120 trees
gbrt = GradientBoostingRegressor(
max_depth=2,
n_estimators=120,
learning_rate=0.1,
random_state=42)
gbrt.fit(X_train, y_train)
# measure MSE validation error at each stage
errors = [mean_squared_error(y_val, y_pred) for y_pred in gbrt.staged_predict(X_val)]
errors
[0.05877146809545241,
0.050146609664278821,
0.042693525239940654,
0.036758764317358611,
0.032342621749728441,
0.028407668512271105,
0.024897554253370889,
0.022344405311247584,
0.019535997367701449,
0.017423553892941333,
0.015298227412102105,
0.013614891608372095,
0.01241865401978786,
0.01114950733723946,
0.010131360091843384,
0.0091854704682465919,
0.0085684302891776056,
0.0078525358395017328,
0.0072105819722258777,
0.0067708705683962693,
0.0062415649764643415,
0.0058360573276457243,
0.0053862983457847987,
0.0051345071507873903,
0.0048692096567381805,
0.0045993749990593299,
0.0043550054844811968,
0.0041542481413648245,
0.0039794595160053785,
0.0038058301746231277,
0.0036528925611761264,
0.0035903310836105469,
0.0035078898256137104,
0.0034145667924260869,
0.0033091498103360911,
0.0032216349333429491,
0.0031684358902285465,
0.0031067035318094903,
0.0030811367114601672,
0.0030602631146299077,
0.003000040093686018,
0.0029246869254349805,
0.0028559321605494477,
0.0028308419421558683,
0.0028218777360194264,
0.0027941065824977074,
0.0027733228935542496,
0.0027805517665357811,
0.0027523772234700978,
0.0027297064654860348,
0.0027248578787871292,
0.0027111390401517179,
0.0027041926119007326,
0.0026930464329994377,
0.0027047076934144398,
0.0027194180251317295,
0.0027010027055809748,
0.0026976053707465464,
0.0026946405089738347,
0.0026713744909731395,
0.0026633491003786457,
0.0026694977341077202,
0.0026594592750579836,
0.0026425819418378605,
0.0026524409142755744,
0.0026418897165154491,
0.0026483360802177103,
0.0026456393608631189,
0.0026465080389023671,
0.0026396693211148074,
0.002649273120700455,
0.002643721514468783,
0.0026463988198929221,
0.0026333618213948747,
0.0026314011519099879,
0.0026349113355268257,
0.0026387528659342825,
0.0026345585421650142,
0.0026355886319374901,
0.0026310345391991532,
0.0026519658939712061,
0.0026467700098620557,
0.00264498239665715,
0.0026475491456891486,
0.0026474836942911913,
0.0026530458155365681,
0.0026478335004093052,
0.0026564768881028435,
0.0026574608795571115,
0.0026537575609276061,
0.0026559108292476983,
0.0026528848367343987,
0.0026533895549644779,
0.0026520896622857252,
0.0026416985817433059,
0.0026497886163651938,
0.0026430582537166087,
0.0026548742317473117,
0.002660275592603878,
0.0026582571161537366,
0.0026570823709750535,
0.0026557538081706522,
0.002675470519360824,
0.0026762761989050578,
0.0026742086578626454,
0.0026957941482744232,
0.0026964801899977998,
0.0026939578807501376,
0.0026959742963617757,
0.0026949319702616616,
0.0026988916344244736,
0.0027169473218451121,
0.0027148017926961689,
0.0027192710134859655,
0.0027358435370699618,
0.0027346474658663323,
0.0027351047440069571,
0.0027459941366245631,
0.0027441324932851491,
0.002756368378237764]
# train another GBRT ensemble using optimal #trees
best_n_estimators = np.argmin(errors)
min_error = errors[best_n_estimators]
gbrt_best = GradientBoostingRegressor(
max_depth=2,
n_estimators=best_n_estimators,
learning_rate=0.1,
random_state=42)
gbrt_best.fit(X_train, y_train)
GradientBoostingRegressor(alpha=0.9, criterion='friedman_mse', init=None,
learning_rate=0.1, loss='ls', max_depth=2, max_features=None,
max_leaf_nodes=None, min_impurity_split=1e-07,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=79, presort='auto',
random_state=42, subsample=1.0, verbose=0, warm_start=False)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.plot(errors, "b.-")
plt.plot([best_n_estimators, best_n_estimators], [0, min_error], "k--")
plt.plot([0, 120], [min_error, min_error], "k--")
plt.plot(best_n_estimators, min_error, "ko")
plt.text(best_n_estimators, min_error*1.2, "Minimum", ha="center", fontsize=14)
plt.axis([0, 120, 0, 0.01])
plt.xlabel("Number of trees")
plt.title("Validation error", fontsize=14)
plt.subplot(122)
plot_predictions([gbrt_best], X, y, axes=[-0.5, 0.5, -0.1, 0.8])
plt.title("Best model (55 trees)", fontsize=14)
#save_fig("early_stopping_gbrt_plot")
plt.show()
- Another method: actually stopping training early
- Implement via warm_start=True (tells Scikit to keep existing trees when fit() is called - allowing incremental training.)
gbrt = GradientBoostingRegressor(
max_depth=2,
n_estimators=1,
learning_rate=0.1,
random_state=42,
warm_start=True)
min_val_error = float("inf")
error_going_up = 0
# 120 estimators.
# stop training with validation error doesn't improve for
# five consecutive iterations
for n_estimators in range(1, 120):
gbrt.n_estimators = n_estimators
gbrt.fit(X_train, y_train)
y_pred = gbrt.predict(X_val)
val_error = mean_squared_error(y_val, y_pred)
if val_error < min_val_error:
min_val_error = val_error
error_going_up = 0
else:
error_going_up += 1
if error_going_up == 5:
break # early stopping
print(gbrt.n_estimators)
59
Stacking
- Instead of using a voting function to aggregate an ensemble's predictor outputs, instead train a model to do the aggregation. ("blending".)
- Blender training: common approach = use a holdout set.
# todo: stacking implementation