%%html
<style>
img[alt=recurrent_unrolled] { width: 400px; }
</style>
<style>
img[alt=sequence_vector] { width: 400px; }
</style>
<style>
img[alt=gru-cell] { width: 400px; }
</style>
<style>
img[alt=encoder-decoder] { width: 400px; }
</style>
Intro
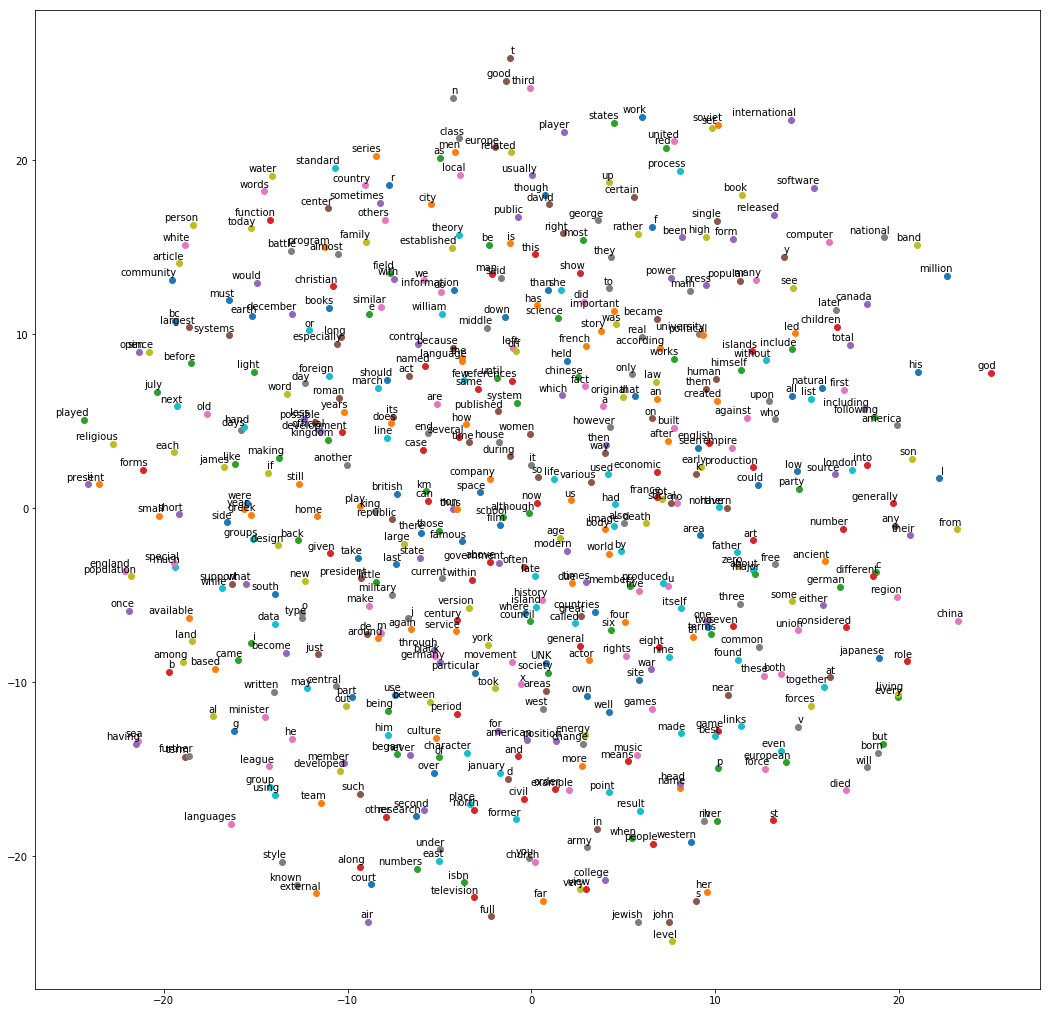
- Use case: arbitrary-length sequence data analysis - anticipation abilities
- RNNs much like feed-forward NNs, but also with backward-facing connections
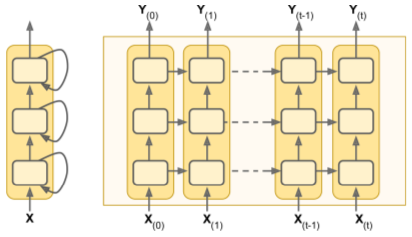
- At time step t each node sees input x(t) plus its previous output y(t-1).
- Below: "unrolling" a net across a time axis.
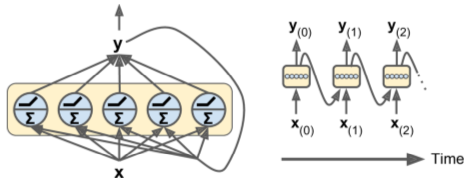
Memory Cells
- A network node that preserves state across time is called a cell (memory cell).
- h(t) is a cell's "hidden" state at time=t.
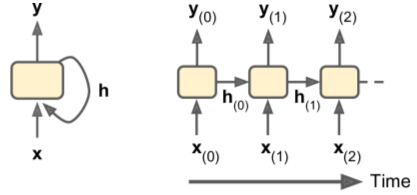
Input/Output Sequences
- RNNs can be used to predict the results of time shifts (sequence-to-sequence), a sentiment score (sequence-to-vector), or image caption (vector-to-sequence).
- sequence-to-vector nets = encoders; vector-to-sequence nets = decoders. One use case: language translation.
- Below:
- Top Left: Sequence-to-sequence
- Top Right: Sequence-to-vector
- Bot Left: Vector-to-sequence
- Bot Right: Delayed-sequence-to-sequence
Basic RNNs in TF
- RNN design: layer of 5 recurrent cells with tanh activation; runs over 2 time steps, and uses vectors of size=3 at each step.
import tensorflow as tf
n_inputs = 3
n_neurons = 5
# two-layer net
X0 = tf.placeholder(tf.float32, [None, n_inputs])
X1 = tf.placeholder(tf.float32, [None, n_inputs])
Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons],dtype=tf.float32))
Wy = tf.Variable(tf.random_normal(shape=[n_neurons,n_neurons],dtype=tf.float32))
b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32))
Y0 = tf.tanh(tf.matmul(X0, Wx) + b)
Y1 = tf.tanh(tf.matmul(Y0, Wy) + tf.matmul(X1, Wx) + b)
init = tf.global_variables_initializer()
# to feed inputs at both time steps,
import numpy as np
# Mini-batch: instance 0,instance 1,instance 2,instance 3
X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]]) # t = 0
X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]]) # t = 1
# Y0, Y1 = network outputs at both time steps
with tf.Session() as sess:
init.run()
Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
print("output at t=0:\n",Y0_val,"\n","output at t=1\n",Y1_val)
output at t=0:
[[-0.77183092 -0.99924457 0.23752896 -0.63130957 -0.83723265]
[-0.92028087 -1. 0.99004787 -0.87230623 -0.99995315]
[-0.97358704 -1. 0.999919 -0.95966864 -1. ]
[ 0.99999094 -0.99890459 0.9991411 0.99996841 -0.99999803]]
output at t=1
[[ 0.99512661 -1. 0.99997395 -0.99830353 -1. ]
[ 0.99977976 0.99013239 -0.96352106 -0.99476629 0.97579277]
[ 0.99981618 -0.99989575 0.99114233 -0.99827981 -0.99984008]
[ 0.54805535 -0.84061396 -0.99912792 -0.47432473 -0.99921536]]
Unrolling through Time (Static) using static_rnn()
tf.reset_default_graph()
n_inputs = 3
n_neurons = 5
X0 = tf.placeholder(tf.float32, [None, n_inputs])
X1 = tf.placeholder(tf.float32, [None, n_inputs])
# BasicRNNCell() -- memcell "factory"
basic_cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons)
# static_rnn() -- creates unrolled RNN net by chaining cells.
# returns 1) python list of output tensors for each time step
# 2) tensor of final network states
output_seqs, states = tf.contrib.rnn.static_rnn(
basic_cell,
[X0, X1],
dtype=tf.float32)
Y0, Y1 = output_seqs
init = tf.global_variables_initializer()
# to feed inputs at both time steps,
import numpy as np
# Mini-batch: instance 0,instance 1,instance 2,instance 3
X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]]) # t = 0
X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]]) # t = 1
# Y0, Y1 = network outputs at both time steps
with tf.Session() as sess:
init.run()
Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
print("output at t=0:\n",Y0_val,"\n","output at t=1\n",Y1_val)
output at t=0:
[[ 0.42442048 0.92431569 -0.2353479 -0.90074939 -0.94408685]
[ 0.73783255 0.98977458 -0.72123086 -0.99919385 -0.99999249]
[ 0.89336294 0.99865782 -0.9186905 -0.99999398 -1. ]
[-0.99143326 -0.99993676 -0.37607926 0.88796568 -0.99899191]]
output at t=1
[[ 0.81709599 0.48319042 -0.96708876 -0.9998284 -1. ]
[-0.18962485 -0.81231028 -0.21763545 0.88739753 0.57306314]
[ 0.17130674 -0.6411857 -0.86380148 -0.95413983 -0.99999553]
[-0.07749119 -0.86547101 -0.00461033 -0.91877526 -0.99582738]]
Simplification
tf.reset_default_graph()
n_steps = 2
n_inputs = 3
n_neurons = 5
# this time, use placeholder with add'l dimension for #timesteps
#X0 = tf.placeholder(tf.float32, [None, n_inputs])
#X1 = tf.placeholder(tf.float32, [None, n_inputs])
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
#print(X)
# transpose - make time steps = 1st dimension
# unstack - extract list of tensors
X_seqs = tf.unstack(
tf.transpose(
X, perm=[1, 0, 2]))
#print(X_seqs)
# BasicRNNCell() -- memcell "factory"
basic_cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons)
# static_rnn() -- creates unrolled RNN net by chaining cells.
# returns 1) python list of output tensors for each time step
# 2) tensor of final network states
output_seqs, states = tf.contrib.rnn.static_rnn(
basic_cell,
X_seqs,
dtype=tf.float32)
#Y0, Y1 = output_seqs
# stack - merge output tensors
# transpose - swap 1st two dimensions
# returns tensor shape [none, #steps, #neurons]
outputs = tf.transpose(
tf.stack(output_seqs),
perm=[1,0,2])
init = tf.global_variables_initializer()
X_batch = np.array([
# t = 0 t = 1
[[0, 1, 2], [9, 8, 7]], # instance 1
[[3, 4, 5], [0, 0, 0]], # instance 2
[[6, 7, 8], [6, 5, 4]], # instance 3
[[9, 0, 1], [3, 2, 1]], # instance 4
])
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
print(outputs_val)
[[[ 0.76157701 0.11581181 0.64773971 -0.79434019 -0.86054337]
[ 0.99998951 -0.66595364 0.99812627 -1. 0.84574401]]
[[ 0.99683905 0.29572889 0.98365188 -0.99992883 -0.88169324]
[ 0.41841054 -0.92049074 -0.64612901 -0.73361856 0.29283327]]
[[ 0.99996316 0.45685658 0.99936479 -1. -0.89980829]
[ 0.99907684 -0.87088716 0.94328976 -0.9999997 0.87934762]]
[[ 0.12318966 0.02264917 0.99982244 -0.99998975 0.99996465]
[ 0.9525854 -0.56515652 0.08665188 -0.99705428 0.87525886]]]
- Above code still not ideal - builds graph with one cell per time step. Ugly & can cause Out Of Memory errors.
Unrolling through Time using dynamic_rnn()
- uses while_loop() to iterate over the memcell
- set swap_memory=True to move GPU memory to CPU during backprop if needed
- accepts single tensor, outputs single tensor - no stack/unstack/transpose ops required.
tf.reset_default_graph()
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
basic_cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(
basic_cell, X, dtype=tf.float32)
init = tf.global_variables_initializer()
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
print(outputs_val)
[[[ 0.01341763 -0.10483158 -0.94257653 0.83843452 -0.20272173]
[ 0.99978089 -0.63150525 -0.99999148 0.99999386 -0.87993085]]
[[ 0.94205797 -0.13386673 -0.9997741 0.99812031 -0.64444101]
[-0.6134249 -0.55738503 0.39783546 0.89031053 0.04465704]]
[[ 0.99817288 -0.16267382 -0.99999928 0.99997997 -0.86824256]
[ 0.99097538 -0.61533296 -0.99695957 0.99986053 -0.64558744]]
[[ 0.9963541 0.23641461 0.75174934 0.98267573 -0.97034496]
[ 0.85169196 -0.07830215 -0.3604137 0.95550352 0.12307668]]]
Variable-Length Input Sequences
- Most problems will have variable length inputs (like sentences).
- This option uses sequence_length param (1D tensor)
tf.reset_default_graph()
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
seq_length = tf.placeholder(tf.int32, [None])
basic_cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(
basic_cell, X, dtype=tf.float32,
#
#
sequence_length=seq_length)
#
#
X_batch = np.array([
[[0, 1, 2], [9, 8, 7]], # instance 1
[[3, 4, 5], [0, 0, 0]], # instance 2 -- zero padded
[[6, 7, 8], [6, 5, 4]], # instance 3
[[9, 0, 1], [3, 2, 1]], # instance 4
])
seq_length_batch = np.array([2,1,2,2])
init = tf.global_variables_initializer()
with tf.Session() as sess:
init.run()
outputs_val, states_val = sess.run(
[outputs, states],
feed_dict={X: X_batch, seq_length: seq_length_batch})
# RNN should output zero vectors for any time step
# beyond input sequence length
print(outputs_val)
[[[ 0.28581977 -0.77421445 -0.34181327 -0.87767971 -0.91387445]
[ 0.99970448 -1. 0.79238343 -1. -0.9997654 ]]
[[ 0.96786171 -0.99937457 -0.03243476 -0.99988878 -0.99875116]
[ 0. 0. 0. 0. 0. ]]
[[ 0.99903995 -0.99999839 0.28328663 -0.99999982 -0.99998271]
[ 0.96896154 -0.99999189 0.43341497 -0.99996883 -0.98279852]]
[[ 0.9976812 -0.99999118 0.99979782 -0.99983948 0.84931362]
[ 0.57188803 -0.99268627 -0.30526906 -0.99518502 0.109933 ]]]
# states tensor contains final state of each cell
print(states_val)
[[ 0.99970448 -1. 0.79238343 -1. -0.9997654 ]
[ 0.96786171 -0.99937457 -0.03243476 -0.99988878 -0.99875116]
[ 0.96896154 -0.99999189 0.43341497 -0.99996883 -0.98279852]
[ 0.57188803 -0.99268627 -0.30526906 -0.99518502 0.109933 ]]
Variable-Length Output Sequences
- Typical output sequence lengths not equal to input lengths
- Most common solution: use end-of-sequence (EOS) token.
RNN Training
- Unroll through time (as shown above) then use backprop through time (BPTT).
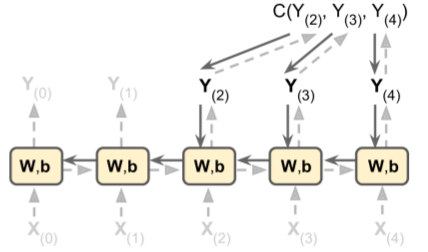
RNN Training: Classifier
- Example: use MNIST (CNN would be better, but lets keep it simple)
- Treat images as 28 rows of 28 pixels each
- Use 150 rnn cells + fully-connected layer of 10 cells (1 per class)
- Followed by softmax layer
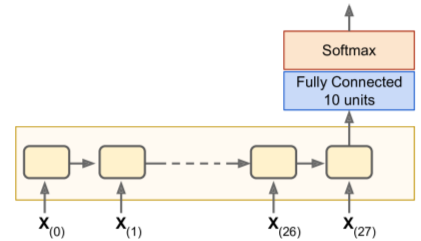
# similar to MNIST classifier
# unrolled RNN replaces hidden layers
tf.reset_default_graph()
from tensorflow.contrib.layers import fully_connected
n_steps = 28
n_inputs = 28
n_neurons = 150
n_outputs = 10
learning_rate = 0.001
# y = placeholder for target classes
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])
basic_cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(
basic_cell, X, dtype=tf.float32)
logits = fully_connected(
states, n_outputs, activation_fn=None)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(
labels=y, logits=logits)
loss = tf.reduce_mean(
xentropy)
optimizer = tf.train.AdamOptimizer(
learning_rate=learning_rate)
training_op = optimizer.minimize(
loss)
correct = tf.nn.in_top_k(
logits, y, 1)
accuracy = tf.reduce_mean(
tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
# load MNIST data, reshape to [batch_size, n_steps, n_inputs]
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
X_test = mnist.test.images.reshape((-1, n_steps, n_inputs))
y_test = mnist.test.labels
Extracting /tmp/data/train-images-idx3-ubyte.gz
Extracting /tmp/data/train-labels-idx1-ubyte.gz
Extracting /tmp/data/t10k-images-idx3-ubyte.gz
Extracting /tmp/data/t10k-labels-idx1-ubyte.gz
# ready to run. reshape each training batch before feeding to net.
n_epochs = 10
batch_size = 150
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
X_batch = X_batch.reshape(
(-1, n_steps, n_inputs))
sess.run(
training_op,
feed_dict={X: X_batch, y: y_batch})
acc_train = accuracy.eval(
feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(
feed_dict={X: X_test, y: y_test})
print(epoch,
"Train accuracy:", acc_train,
"Test accuracy:", acc_test)
0 Train accuracy: 0.953333 Test accuracy: 0.8711
1 Train accuracy: 0.953333 Test accuracy: 0.9417
2 Train accuracy: 0.953333 Test accuracy: 0.9432
3 Train accuracy: 0.946667 Test accuracy: 0.9595
4 Train accuracy: 0.98 Test accuracy: 0.9627
5 Train accuracy: 0.966667 Test accuracy: 0.9666
6 Train accuracy: 0.96 Test accuracy: 0.961
7 Train accuracy: 0.973333 Test accuracy: 0.9729
8 Train accuracy: 0.986667 Test accuracy: 0.9702
9 Train accuracy: 0.986667 Test accuracy: 0.9732
RNN Training: Predicting Time Series
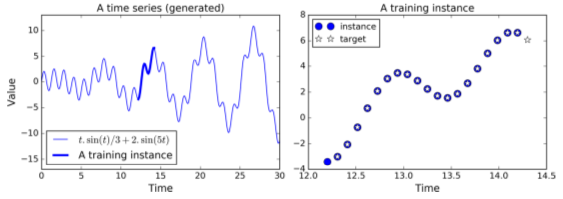
t_min, t_max = 0, 30
resolution = 0.1
def time_series(t):
return t * np.sin(t) / 3 + 2 * np.sin(t*5)
def next_batch(batch_size, n_steps):
t0 = np.random.rand(batch_size, 1) * (t_max - t_min - n_steps * resolution)
Ts = t0 + np.arange(0., n_steps + 1) * resolution
ys = time_series(Ts)
return ys[:, :-1].reshape(-1, n_steps, 1), ys[:, 1:].reshape(-1, n_steps, 1)
t = np.linspace(t_min, t_max, (t_max - t_min) // resolution)
n_steps = 20
t_instance = np.linspace(
12.2, 12.2 + resolution * (n_steps + 1), n_steps + 1)
# each training instance = 20 inputs long
# targets = 20-input sequences
tf.reset_default_graph()
n_steps = 20
n_inputs = 1
n_neurons = 100
n_outputs = 1
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])
cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons,
activation=tf.nn.relu)
outputs, states = tf.nn.dynamic_rnn(
cell, X, dtype=tf.float32)
print(outputs.shape)
(?, 20, 100)
# output at each time step now vector[100],
# but we want single output value at each step.
# use OutputProjectionWrapper()
# -- adds FC layer to top of each output
cell = tf.contrib.rnn.OutputProjectionWrapper(
tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons,
activation=tf.nn.relu),
output_size=n_outputs)
# define cost function using MSE
# use Adam optimizer
learning_rate = 0.001
loss = tf.reduce_mean(
tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(
learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
init = tf.global_variables_initializer()
# initialize & run
init = tf.global_variables_initializer()
n_iterations = 1000
batch_size = 50
with tf.Session() as sess:
init.run()
for iteration in range(n_iterations):
X_batch, y_batch = next_batch(batch_size, n_steps)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if iteration % 100 == 0:
mse = loss.eval(feed_dict={X: X_batch, y: y_batch})
print(iteration, "\tMSE:", mse)
# use trained model to make some predictions
X_new = time_series(np.array(t_instance[:-1].reshape(-1, n_steps, n_inputs)))
y_pred = sess.run(outputs, feed_dict={X: X_new})
print(y_pred)
0 MSE: 15.3099
100 MSE: 13.5276
200 MSE: 11.0956
300 MSE: 9.91156
400 MSE: 14.0311
500 MSE: 9.73811
600 MSE: 9.23351
700 MSE: 9.64445
800 MSE: 8.98904
900 MSE: 10.849
[[[ 0. 0. 0. ..., 0. 0. 0. ]
[ 0. 0.04218276 0. ..., 0. 0. 0. ]
[ 0. 0.14342034 0. ..., 0. 0. 0. ]
...,
[ 6.67315388 0. 6.39087296 ..., 6.9017005 6.30435514
6.23329258]
[ 6.61708975 0. 6.31429434 ..., 6.58116341 6.19745445
6.11896658]
[ 5.9406209 0. 5.73649979 ..., 5.63920403 5.5386672
5.47510672]]]
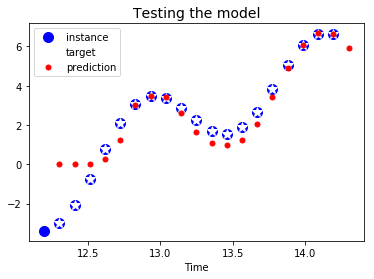
import matplotlib.pyplot as plt
plt.title("Testing the model", fontsize=14)
plt.plot(
t_instance[:-1],
time_series(t_instance[:-1]),
"bo", markersize=10, label="instance")
plt.plot(
t_instance[1:],
time_series(t_instance[1:]),
"w*", markersize=10, label="target")
plt.plot(
t_instance[1:],
y_pred[0,:,0],
"r.", markersize=10, label="prediction")
plt.legend(loc="upper left")
plt.xlabel("Time")
#save_fig("time_series_pred_plot")
plt.show()
- OutputProjectionWrapper() = simplest solution for reducing output sequences to one value/timestep, but not most efficient.
- More efficient solution shown below - signficant speed boost.
tf.reset_default_graph()
n_steps = 20
n_inputs = 1
n_neurons = 100
n_outputs = 1
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])
cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons,
activation=tf.nn.relu)
rnn_outputs, states = tf.nn.dynamic_rnn(
cell, X, dtype=tf.float32)
# stack outputs using reshape
stacked_rnn_outputs = tf.reshape(
rnn_outputs, [-1, n_neurons])
print(stacked_rnn_outputs)
# add FC layer -- just a projection, so no activation fn needed
stacked_outputs = fully_connected(
stacked_rnn_outputs,
n_outputs,
activation_fn=None)
print(stacked_outputs)
# unstack outputs using reshape
outputs = tf.reshape(
stacked_outputs, [-1, n_steps, n_outputs])
print(outputs)
loss = tf.reduce_sum(tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
#initialize & run
init = tf.global_variables_initializer()
n_iterations = 1000
batch_size = 50
with tf.Session() as sess:
init.run()
for iteration in range(n_iterations):
X_batch, y_batch = next_batch(batch_size, n_steps)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if iteration % 100 == 0:
mse = loss.eval(feed_dict={X: X_batch, y: y_batch})
print(iteration, "\tMSE:", mse)
# use trained model to make some predictions
X_new = time_series(np.array(t_instance[:-1].reshape(-1, n_steps, n_inputs)))
y_pred = sess.run(outputs, feed_dict={X: X_new})
print(y_pred)
Tensor("Reshape:0", shape=(?, 100), dtype=float32)
Tensor("fully_connected/BiasAdd:0", shape=(?, 1), dtype=float32)
Tensor("Reshape_1:0", shape=(?, 20, 1), dtype=float32)
0 MSE: 22963.7
100 MSE: 743.444
200 MSE: 276.131
300 MSE: 117.955
400 MSE: 53.3529
500 MSE: 63.4189
600 MSE: 45.1415
700 MSE: 41.5129
800 MSE: 53.4219
900 MSE: 43.2203
[[[-3.46527553]
[-2.46867704]
[-1.10144436]
[ 0.69717044]
[ 2.08823276]
[ 3.13628578]
[ 3.55210543]
[ 3.4186697 ]
[ 2.85978389]
[ 2.15520501]
[ 1.67705297]
[ 1.6919663 ]
[ 1.93633199]
[ 2.70151305]
[ 3.87054777]
[ 5.11770582]
[ 6.15701818]
[ 6.71814394]
[ 6.69798708]
[ 6.08309698]]]
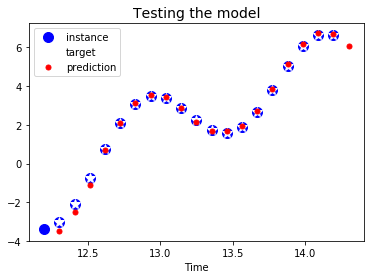
plt.title("Testing the model", fontsize=14)
plt.plot(t_instance[:-1], time_series(t_instance[:-1]), "bo", markersize=10, label="instance")
plt.plot(t_instance[1:], time_series(t_instance[1:]), "w*", markersize=10, label="target")
plt.plot(t_instance[1:], y_pred[0,:,0], "r.", markersize=10, label="prediction")
plt.legend(loc="upper left")
plt.xlabel("Time")
plt.show()
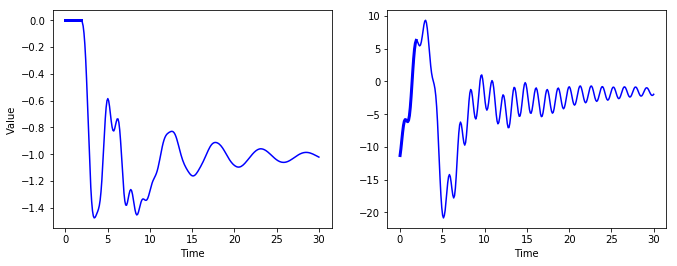
Creative RNNs
- Use model to generate creative sequences
- Provide seed sequence of length = n_steps, zero-filled
- use model to append predicted new value to sequence
- feed last n_steps values to model to predict next value, etc.
- should get new sequence resembling original time series
n_iterations = 2000
batch_size = 50
with tf.Session() as sess:
init.run()
for iteration in range(n_iterations):
X_batch, y_batch = next_batch(batch_size, n_steps)
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
if iteration % 100 == 0:
mse = loss.eval(feed_dict={X: X_batch, y: y_batch})
print(iteration, "\tMSE:", mse)
sequence1 = [0. for i in range(n_steps)]
for iteration in range(len(t) - n_steps):
X_batch = np.array(sequence1[-n_steps:]).reshape(1, n_steps, 1)
y_pred = sess.run(outputs, feed_dict={X: X_batch})
sequence1.append(y_pred[0, -1, 0])
sequence2 = [time_series(i * resolution + t_min + (t_max-t_min/3)) for i in range(n_steps)]
for iteration in range(len(t) - n_steps):
X_batch = np.array(sequence2[-n_steps:]).reshape(1, n_steps, 1)
y_pred = sess.run(outputs, feed_dict={X: X_batch})
sequence2.append(y_pred[0, -1, 0])
plt.figure(figsize=(11,4))
plt.subplot(121)
plt.plot(t, sequence1, "b-")
plt.plot(t[:n_steps], sequence1[:n_steps], "b-", linewidth=3)
plt.xlabel("Time")
plt.ylabel("Value")
plt.subplot(122)
plt.plot(t, sequence2, "b-")
plt.plot(t[:n_steps], sequence2[:n_steps], "b-", linewidth=3)
plt.xlabel("Time")
#save_fig("creative_sequence_plot")
plt.show()
0 MSE: 14607.1
100 MSE: 505.605
200 MSE: 167.29
300 MSE: 83.1336
400 MSE: 58.9695
500 MSE: 61.0224
600 MSE: 55.8671
700 MSE: 43.7078
800 MSE: 57.2013
900 MSE: 55.3992
1000 MSE: 54.082
1100 MSE: 55.48
1200 MSE: 39.4618
1300 MSE: 40.7414
1400 MSE: 47.8548
1500 MSE: 43.9252
1600 MSE: 47.892
1700 MSE: 42.0762
1800 MSE: 48.2429
1900 MSE: 42.7509
Deep RNNs
- Built by stacking cells into a MultiRNNCell().
tf.reset_default_graph()
n_inputs = 2
n_neurons = 100
n_layers = 3
n_steps = 5
keep_prob = 0.5
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
basic_cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons)
print(basic_cell)
multi_layer_cell = tf.contrib.rnn.MultiRNNCell(
[basic_cell] * n_layers)
print(multi_layer_cell)
# states = tuple (one tensor/layer, = final state of layer's cell)
outputs, states = tf.nn.dynamic_rnn(
multi_layer_cell, X, dtype=tf.float32)
init = tf.global_variables_initializer()
import numpy.random as rnd
X_batch = rnd.rand(2, n_steps, n_inputs)
with tf.Session() as sess:
init.run()
outputs_val, states_val = sess.run(
[outputs, states],
feed_dict={X: X_batch})
print(outputs_val.shape)
<tensorflow.contrib.rnn.python.ops.core_rnn_cell_impl.BasicRNNCell object at 0x7fd1ff3dbb00>
<tensorflow.contrib.rnn.python.ops.core_rnn_cell_impl.MultiRNNCell object at 0x7fd1d9b7c9e8>
(2, 5, 100)
DRNNs: Multiple GPUs
- TO DO
Dropout
- Very deep RNNs = danger of overfit. Use dropout to avoid problem.
- Can apply before or after RNN
- If applying dropout between RNN layers, need to use DropoutWrapper.
# apply 50% dropout to inputs of RNN layers
# can apply dropout to outputs via output_keep_prob
tf.reset_default_graph()
from tensorflow.contrib.layers import fully_connected
n_inputs = 1
n_neurons = 100
n_layers = 3
n_steps = 20
n_outputs = 1
keep_prob = 0.5
learning_rate = 0.001
def deep_rnn_with_dropout(X, y, is_training):
# TF implementation of DropoutWrapper doesn't differentiate
# between training & testing.
cell = tf.contrib.rnn.BasicRNNCell(
num_units=n_neurons)
if is_training:
cell = tf.contrib.rnn.DropoutWrapper(
cell, input_keep_prob=keep_prob)
#
#
multi_layer_cell = tf.contrib.rnn.MultiRNNCell(
[cell] * n_layers)
rnn_outputs, states = tf.nn.dynamic_rnn(
multi_layer_cell, X, dtype=tf.float32)
stacked_rnn_outputs = tf.reshape(
rnn_outputs, [-1, n_neurons])
stacked_outputs = fully_connected(
stacked_rnn_outputs, n_outputs, activation_fn=None)
outputs = tf.reshape(
stacked_outputs, [-1, n_steps, n_outputs])
loss = tf.reduce_sum(
tf.square(outputs - y))
optimizer = tf.train.AdamOptimizer(
learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
return outputs, loss, training_op
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_steps, n_outputs])
outputs, loss, training_op = deep_rnn_with_dropout(X, y, is_training)
init = tf.global_variables_initializer()
saver = tf.train.Saver()
- Dropout, in this code, works during both training & testing (don't want).
- dropout_wrapper() doesn't know how to handle this, so you need one graph for training, another for testing.
n_iterations = 2000
batch_size = 50
is_training = True
with tf.Session() as sess:
if is_training:
init.run()
for iteration in range(n_iterations):
X_batch, y_batch = next_batch(batch_size, n_steps)
sess.run(
training_op,
feed_dict={X: X_batch, y: y_batch})
if iteration % 100 == 0:
mse = loss.eval(
feed_dict={X: X_batch, y: y_batch})
print(iteration, "\tMSE:", mse)
save_path = saver.save(sess, "/tmp/my_model.ckpt")
else:
saver.restore(sess, "/tmp/my_model.ckpt")
X_new = time_series(
np.array(t_instance[:-1].reshape(-1, n_steps, n_inputs)))
y_pred = sess.run(
outputs, feed_dict={X: X_new})
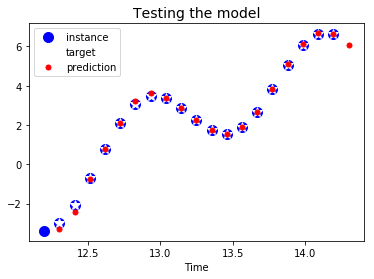
plt.title("Testing the model", fontsize=14)
plt.plot(t_instance[:-1], time_series(t_instance[:-1]), "bo", markersize=10, label="instance")
plt.plot(t_instance[1:], time_series(t_instance[1:]), "w*", markersize=10, label="target")
plt.plot(t_instance[1:], y_pred[0,:,0], "r.", markersize=10, label="prediction")
plt.legend(loc="upper left")
plt.xlabel("Time")
plt.show()
0 MSE: 10428.8
100 MSE: 314.521
200 MSE: 152.328
300 MSE: 155.774
400 MSE: 100.226
500 MSE: 80.2064
600 MSE: 92.3898
700 MSE: 55.4301
800 MSE: 50.8537
900 MSE: 47.1413
1000 MSE: 57.1007
1100 MSE: 64.2314
1200 MSE: 51.3272
1300 MSE: 51.1612
1400 MSE: 41.0518
1500 MSE: 42.267
1600 MSE: 29.6838
1700 MSE: 48.4316
1800 MSE: 46.5584
1900 MSE: 40.6252
# testing
with tf.Session() as sess:
saver.restore(sess, "/tmp/my_model.ckpt")
X_new = time_series(
np.array(t_instance[:-1].reshape(-1, n_steps, n_inputs)))
y_pred = sess.run(
outputs, feed_dict={X: X_new})
plt.title("Testing the model", fontsize=14)
plt.plot(t_instance[:-1], time_series(t_instance[:-1]), "bo", markersize=10, label="instance")
plt.plot(t_instance[1:], time_series(t_instance[1:]), "w*", markersize=10, label="target")
plt.plot(t_instance[1:], y_pred[0,:,0], "r.", markersize=10, label="prediction")
plt.legend(loc="upper left")
plt.xlabel("Time")
plt.show()
Training across Many Time Steps
- problem #1: RNNs susceptible to vanishing/exploding gradients issues. Previous tricks will work, but training time = prohibitively long for even modest sequences.
- solution #1: truncated backprop thru time (unrolling RNN over limited number of timesteps during training). Works, but model will not be able to learn long-term patterns.
- problem #2: memory of early inputs fades away - information lost during each transformation.
- solution #2: using a long-term memory cell.
Long Short-Term Memory (LSTM) Cell
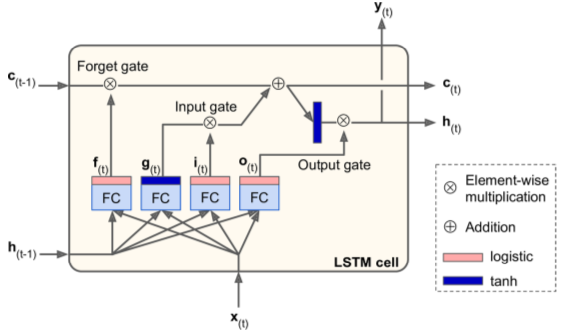
implemented via BasicLSTMCell() instead of BasicRNNCell().
key feature: net learns what to store (long-term), what to read from, what to throw away.
- Four FC layers - each with unique purposes:
- main layer: outputs g(t)
- forget gate: controlled by f(t) - decides which parts of long-term memory to erase
- input gate: controlled by i(t) - decides which parts of g(t) to add to long-term memory
- output gate: controlled by o(t) - decides which parts of long-term state should be read & outputted at this time step.
tf.reset_default_graph()
from tensorflow.contrib.layers import fully_connected
n_steps = 28
n_inputs = 28
n_neurons = 150
n_outputs = 10
learning_rate = 0.001
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])
lstm_cell = tf.contrib.rnn.BasicLSTMCell(
num_units=n_neurons)
multi_cell = tf.contrib.rnn.MultiRNNCell(
[lstm_cell]*3)
outputs, states = tf.nn.dynamic_rnn(
multi_cell, X, dtype=tf.float32)
top_layer_h_state = states[-1][1]
logits = fully_connected(
top_layer_h_state,
n_outputs,
activation_fn=None, scope="softmax")
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(
labels=y, logits=logits)
loss = tf.reduce_mean(
xentropy, name="loss")
optimizer = tf.train.AdamOptimizer(
learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(
logits, y, 1)
accuracy = tf.reduce_mean(
tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
states
(LSTMStateTuple(c=<tf.Tensor 'rnn/while/Exit_2:0' shape=(?, 150) dtype=float32>, h=<tf.Tensor 'rnn/while/Exit_3:0' shape=(?, 150) dtype=float32>),
LSTMStateTuple(c=<tf.Tensor 'rnn/while/Exit_4:0' shape=(?, 150) dtype=float32>, h=<tf.Tensor 'rnn/while/Exit_5:0' shape=(?, 150) dtype=float32>),
LSTMStateTuple(c=<tf.Tensor 'rnn/while/Exit_6:0' shape=(?, 150) dtype=float32>, h=<tf.Tensor 'rnn/while/Exit_7:0' shape=(?, 150) dtype=float32>))
top_layer_h_state
<tf.Tensor 'rnn/while/Exit_7:0' shape=(?, 150) dtype=float32>
n_epochs = 10
batch_size = 150
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
X_batch = X_batch.reshape((batch_size, n_steps, n_inputs))
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
print("Epoch", epoch, "Train accuracy =", acc_train, "Test accuracy =", acc_test)
Epoch 0 Train accuracy = 0.966667 Test accuracy = 0.9403
Epoch 1 Train accuracy = 0.98 Test accuracy = 0.9742
Epoch 2 Train accuracy = 0.993333 Test accuracy = 0.979
Epoch 3 Train accuracy = 0.993333 Test accuracy = 0.9805
Epoch 4 Train accuracy = 1.0 Test accuracy = 0.9854
Epoch 5 Train accuracy = 0.98 Test accuracy = 0.9827
Epoch 6 Train accuracy = 0.993333 Test accuracy = 0.9851
Epoch 7 Train accuracy = 1.0 Test accuracy = 0.9865
Epoch 8 Train accuracy = 1.0 Test accuracy = 0.9887
Epoch 9 Train accuracy = 0.993333 Test accuracy = 0.9871
Peephole Connections
- Basic LSTM cell: gate controllers only see input x(t) & prev short-term state h(t-1).
- Improvement: let gate peek at long-term state too. Provided with previous long-term state c(t-1) as inputs to forget gate & input gate; current long-term state c(t) added as input to output gate controller.
# Peepholes in TF
lstm_cell = tf.contrib.rnn.LSTMCell(
num_units=n_neurons,
use_peepholes=True)
Gated Recurrent Unit (GRU) Cell
- Simplified version of LSTM cell
- State vectors merged into single h(t).
- Single gate controller manages forget gate & input gate. (if a memory is to be stored, its location is erased first.)
- No output gate - full state vector output on
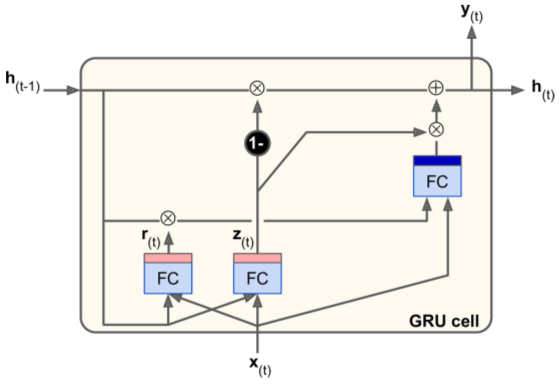
# in TF
gru_cell = tf.contrib.rnn.GRUCell(num_units=n_neurons)
Natural Language Processing (NLP)
- Mostly based on RNNs
- See Word2Vec and Seq2Seq tutorials!
- More: Chris Olah, Sebastian Ruder
Word Embeddings
- First: need a word representation. Similar words should have similar representations.
- Common sol'n: each word in vocab = small, dense vector of embeddings.
# create embeddings variable. init with random[-1,+1]
vocabulary_size = 50000
embedding_size = 150
embeddings = tf.Variable(
tf.random_uniform(
[vocabulary_size, embedding_size],
-1.0, 1.0))
- Feeding new sentences to net: replace unknown words, numbers, URLs, etc with predefined tokens. Once a word is known, you can look it up in a dictionary.
train_inputs = tf.placeholder(
tf.int32, shape=[None]) # from ids...
embed = tf.nn.embedding_lookup(
embeddings, train_inputs) # ...to embeddings
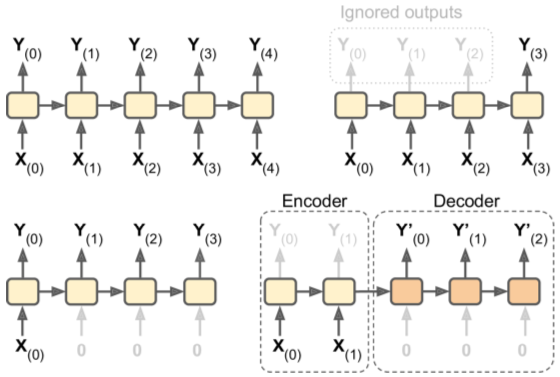
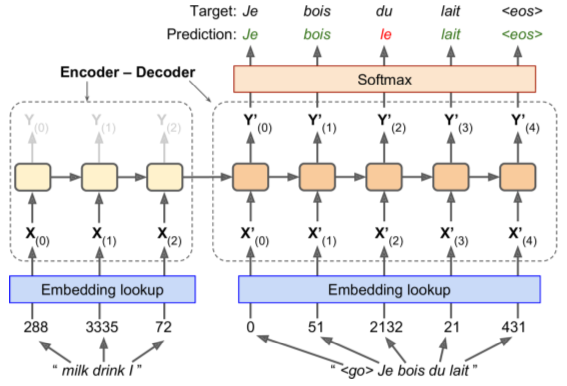
English => French Encoder-Decoder Network (link)
- English inputs, French outputs
- French translations also fed, pushed back one step
- English sentences reversed before entry (ensures beginning of sentence is fed last = best for decoder translation)
- Decoder returns score for each word in output vocabulary - softmax turns them into probabilities. Highest probability word is returned.
from six.moves import urllib
import errno
import os
import zipfile
WORDS_PATH = "datasets/words"
WORDS_URL = 'http://mattmahoney.net/dc/text8.zip'
def mkdir_p(path):
"""Create directories, ok if they already exist.
This is for python 2 support. In python >=3.2, simply use:
>>> os.makedirs(path, exist_ok=True)
"""
try:
os.makedirs(path)
except OSError as exc:
if exc.errno == errno.EEXIST and os.path.isdir(path):
pass
else:
raise
def fetch_words_data(words_url=WORDS_URL, words_path=WORDS_PATH):
os.makedirs(words_path, exist_ok=True)
zip_path = os.path.join(words_path, "words.zip")
if not os.path.exists(zip_path):
urllib.request.urlretrieve(words_url, zip_path)
with zipfile.ZipFile(zip_path) as f:
data = f.read(f.namelist()[0])
return data.decode("ascii").split()
words = fetch_words_data()
words[:5]
['anarchism', 'originated', 'as', 'a', 'term']
Build dictionary
from collections import Counter
vocabulary_size = 50000
vocabulary = [("UNK", None)] + Counter(words).most_common(vocabulary_size - 1)
vocabulary = np.array([word for word, _ in vocabulary])
dictionary = {word: code for code, word in enumerate(vocabulary)}
data = np.array([dictionary.get(word, 0) for word in words])
" ".join(words[:9]), data[:9]
('anarchism originated as a term of abuse first used',
array([5244, 3081, 12, 6, 195, 2, 3135, 46, 59]))
" ".join([vocabulary[word_index] for word_index in [5241, 3081, 12, 6, 195, 2, 3134, 46, 59]])
'anywhere originated as a term of presidency first used'
words[24], data[24]
('culottes', 0)
Generate batches
import random
from collections import deque
def generate_batch(batch_size, num_skips, skip_window):
global data_index
assert batch_size % num_skips == 0
assert num_skips <= 2 * skip_window
batch = np.ndarray(shape=(batch_size), dtype=np.int32)
labels = np.ndarray(shape=(batch_size, 1), dtype=np.int32)
span = 2 * skip_window + 1 # [ skip_window target skip_window ]
buffer = deque(maxlen=span)
for _ in range(span):
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
for i in range(batch_size // num_skips):
target = skip_window # target label at the center of the buffer
targets_to_avoid = [ skip_window ]
for j in range(num_skips):
while target in targets_to_avoid:
target = random.randint(0, span - 1)
targets_to_avoid.append(target)
batch[i * num_skips + j] = buffer[skip_window]
labels[i * num_skips + j, 0] = buffer[target]
buffer.append(data[data_index])
data_index = (data_index + 1) % len(data)
return batch, labels
data_index=0
batch, labels = generate_batch(8, 2, 1)
batch, [vocabulary[word] for word in batch]
(array([3081, 3081, 12, 12, 6, 6, 195, 195], dtype=int32),
['originated', 'originated', 'as', 'as', 'a', 'a', 'term', 'term'])
labels, [vocabulary[word] for word in labels[:, 0]]
(array([[5244],
[ 12],
[ 6],
[3081],
[ 195],
[ 12],
[ 6],
[ 2]], dtype=int32),
['anarchism', 'as', 'a', 'originated', 'term', 'as', 'a', 'of'])
Build the Model
batch_size = 128
embedding_size = 128 # Dimension of the embedding vector.
skip_window = 1 # How many words to consider left and right.
num_skips = 2 # How many times to reuse an input to generate a label.
# We pick a random validation set to sample nearest neighbors. Here we limit the
# validation samples to the words that have a low numeric ID, which by
# construction are also the most frequent.
valid_size = 16 # Random set of words to evaluate similarity on.
valid_window = 100 # Only pick dev samples in the head of the distribution.
valid_examples = rnd.choice(valid_window, valid_size, replace=False)
num_sampled = 64 # Number of negative examples to sample.
learning_rate = 0.01
tf.reset_default_graph()
# Input data.
train_inputs = tf.placeholder(tf.int32, shape=[batch_size])
train_labels = tf.placeholder(tf.int32, shape=[batch_size, 1])
valid_dataset = tf.constant(valid_examples, dtype=tf.int32)
# Look up embeddings for inputs.
init_embeddings = tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0)
embeddings = tf.Variable(init_embeddings)
embed = tf.nn.embedding_lookup(embeddings, train_inputs)
# Construct the variables for the NCE loss
nce_weights = tf.Variable(
tf.truncated_normal([vocabulary_size, embedding_size],
stddev=1.0 / np.sqrt(embedding_size)))
nce_biases = tf.Variable(tf.zeros([vocabulary_size]))
# Compute the average NCE loss for the batch.
# tf.nce_loss automatically draws a new sample of the negative labels each
# time we evaluate the loss.
loss = tf.reduce_mean(
tf.nn.nce_loss(nce_weights, nce_biases, train_labels, embed,
num_sampled, vocabulary_size))
# Construct the Adam optimizer
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
# Compute the cosine similarity between minibatch examples and all embeddings.
norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), axis=1, keep_dims=True))
normalized_embeddings = embeddings / norm
valid_embeddings = tf.nn.embedding_lookup(normalized_embeddings, valid_dataset)
similarity = tf.matmul(valid_embeddings, normalized_embeddings, transpose_b=True)
# Add variable initializer.
init = tf.global_variables_initializer()
num_steps = 1000 # was 100000?
with tf.Session() as session:
init.run()
average_loss = 0
for step in range(num_steps):
print("\rIteration: {}".format(step), end="\t")
batch_inputs, batch_labels = generate_batch(batch_size, num_skips, skip_window)
feed_dict = {train_inputs : batch_inputs, train_labels : batch_labels}
# We perform one update step by evaluating the training op (including it
# in the list of returned values for session.run()
_, loss_val = session.run([training_op, loss], feed_dict=feed_dict)
average_loss += loss_val
if step % 2000 == 0:
if step > 0:
average_loss /= 2000
# The average loss is an estimate of the loss over the last 2000 batches.
print("Average loss at step ", step, ": ", average_loss)
average_loss = 0
# Note that this is expensive (~20% slowdown if computed every 500 steps)
if step % 10000 == 0:
sim = similarity.eval()
for i in range(valid_size):
valid_word = vocabulary[valid_examples[i]]
top_k = 8 # number of nearest neighbors
nearest = (-sim[i, :]).argsort()[1:top_k+1]
log_str = "Nearest to %s:" % valid_word
for k in range(top_k):
close_word = vocabulary[nearest[k]]
log_str = "%s %s," % (log_str, close_word)
print(log_str)
final_embeddings = normalized_embeddings.eval()
Iteration: 0 Average loss at step 0 : 260.603485107
Nearest to and: marsh, sipe, vehement, exercises, einer, mrnas, dancer, grendel,
Nearest to called: innuendo, algerian, synthesizing, montgomery, unspoken, elevating, plankton, monochromatic,
Nearest to many: salinas, fuji, trochaic, rubinstein, eln, tintin, lloyd, carbides,
Nearest to about: moreover, congo, choctaws, accomplished, unwieldy, ks, halifax, pac,
Nearest to than: awake, exact, offutt, gloster, pronunciations, delight, tsarina, hopped,
Nearest to or: long, mage, warriors, adhering, sk, clitoridectomy, parenting, vanguard,
Nearest to of: shakespeare, kemp, relax, cul, breakaway, solemnly, mason, mng,
Nearest to when: tolstoy, courtesan, hashes, coursing, evi, ren, diurnal, stimson,
Nearest to four: supermassive, soviet, palatalization, acclaimed, aided, whitney, filtration, lesbians,
Nearest to most: din, hawaii, loch, necronomicon, sunnah, sh, onager, miracles,
Nearest to on: helpers, tangle, heretical, compulsion, unorganized, rump, intimidating, israeli,
Nearest to but: ohio, rican, politeness, watkins, ingesting, street, hatred, novices,
Nearest to that: xhosa, distressed, continually, fausto, iole, admitted, etsi, gross,
Nearest to all: orissa, persistent, moro, informative, reservation, ren, browne, frobenius,
Nearest to in: chanced, accelerator, sergio, demonstrating, inertia, jarrett, intricate, orange,
Nearest to had: irredentist, kbit, sarris, lactate, bettor, narratives, hui, transpired,
Iteration: 999
Save final embeddings
np.save("my_final_embeddings.npy", final_embeddings)
Plot embeddings
def plot_with_labels(low_dim_embs, labels):
assert low_dim_embs.shape[0] >= len(labels), "More labels than embeddings"
plt.figure(figsize=(18, 18)) #in inches
for i, label in enumerate(labels):
x, y = low_dim_embs[i,:]
plt.scatter(x, y)
plt.annotate(label,
xy=(x, y),
xytext=(5, 2),
textcoords='offset points',
ha='right',
va='bottom')
plt.show()
from sklearn.manifold import TSNE
tsne = TSNE(perplexity=30, n_components=2, init='pca', n_iter=5000)
plot_only = 500
low_dim_embs = tsne.fit_transform(final_embeddings[:plot_only,:])
labels = [vocabulary[i] for i in range(plot_only)]
plot_with_labels(low_dim_embs, labels)