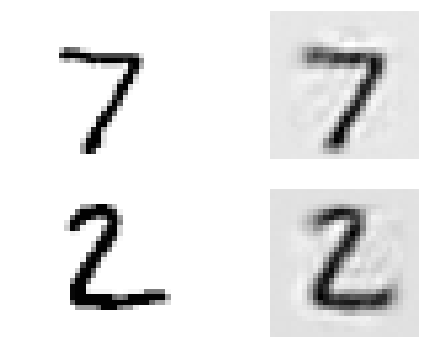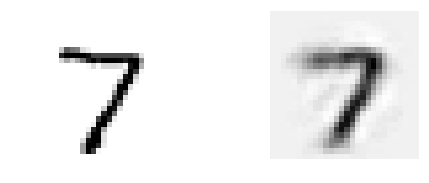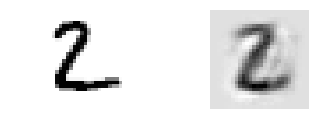import matplotlib.pyplot as plt
import numpy as np
import numpy.random as rnd
import tensorflow as tf
import sys

Data Representations

Much easier to remember sequence patterns than to remember exact lists. First studied as chess game positions (1970s).
Autoencoder converts inputs to internal shorthand, then returns best-guess similarity. Two parts: encoder (recognizer) & decoder (generator, aka reconstructor).
Reconstruction loss - penalizes model when reconstructions /= inputs.
Internal representation = lower dimensionality, so AE is forced to learn most important features in inputs.

PCA with Undercomplete Linear Autoencoder

# lets build a 3D dataset

rnd.seed(4)
m = 100
w1, w2 = 0.1, 0.3
noise = 0.1

angles = rnd.rand(m) * 3 * np.pi / 2 - 0.5
X_train = np.empty((m, 3))
X_train[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * rnd.randn(m) / 2
X_train[:, 1] = np.sin(angles) * 0.7 + noise * rnd.randn(m) / 2
X_train[:, 2] = X_train[:, 0] * w1 + X_train[:, 1] * w2 + noise * rnd.randn(m)

# normalize it

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)

plt.plot(X_train)
plt.show()

# build AE

from tensorflow.contrib.layers import fully_connected

n_inputs = 3 # 3D inputs
n_hidden = 2 # 2D codings
n_outputs = n_inputs

learning_rate = 0.01

X = tf.placeholder(
    tf.float32, shape=[None, n_inputs])

#
# set activation_fn=None & use MSE for cost function
# to perform simple PCA.
#

hidden = fully_connected(
    X, 
    n_hidden, 
    activation_fn=None)

outputs = fully_connected(
    hidden, 
    n_outputs, 
    activation_fn=None)

# MSE
reconstruction_loss = tf.reduce_mean(
    tf.square(outputs - X))

optimizer = tf.train.AdamOptimizer(
    learning_rate)

training_op = optimizer.minimize(
    reconstruction_loss)

init = tf.global_variables_initializer()

# run the AE

n_iterations = 10000
codings = hidden

with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        training_op.run(feed_dict={X: X_train})
    codings_val = codings.eval(feed_dict={X: X_train})

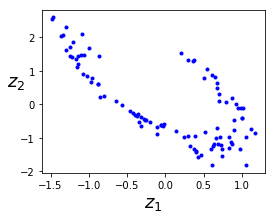
fig = plt.figure(figsize=(4,3))
plt.plot(codings_val[:,0], codings_val[:, 1], "b.")
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18, rotation=0)
#ave_fig("linear_autoencoder_pca_plot")
plt.show()

# plot: 2D projection with max variance

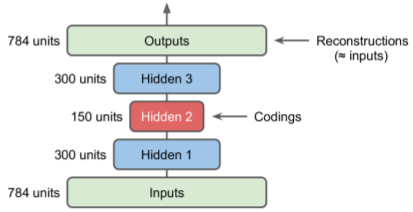
Stacked Autoencoders

AEs with multiple hidden layers - for more complex model learning

tf.reset_default_graph()

n_inputs      = 28 * 28 # for MNIST
n_hidden1     = 300
n_hidden2     = 150 # codings
n_hidden3     = n_hidden1
n_outputs     = n_inputs
learning_rate = 0.01
l2_reg        = 0.0001

X = tf.placeholder(tf.float32, 
                   shape=[None, n_inputs])

with tf.contrib.framework.arg_scope(
    [fully_connected],
    activation_fn=tf.nn.elu,
    weights_initializer=tf.contrib.layers.variance_scaling_initializer(),
    weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg)):

    hidden1 = fully_connected(X,       n_hidden1)
    hidden2 = fully_connected(hidden1, n_hidden2) # codings
    hidden3 = fully_connected(hidden2, n_hidden3)
    outputs = fully_connected(hidden3, n_outputs, activation_fn=None)

# MSE
reconstruction_loss = tf.reduce_mean(
    tf.square(outputs - X))

reg_losses = tf.get_collection(
    tf.GraphKeys.REGULARIZATION_LOSSES)

loss = tf.add_n(
    [reconstruction_loss] + reg_losses)

optimizer = tf.train.AdamOptimizer(
    learning_rate)

training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()
saver = tf.train.Saver()

# use MNIST dataset 

from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets("/tmp/data/")

# train the net. digit labels (y_batch) = unused.

n_epochs = 4
batch_size = 150

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        n_batches = mnist.train.num_examples // batch_size
        for iteration in range(n_batches):
            print("\r{}%".format(100 * iteration // n_batches), end="")
            sys.stdout.flush()
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={X: X_batch})
        mse_train = reconstruction_loss.eval(feed_dict={X: X_batch})
        print("\r{}".format(epoch), "Train MSE:", mse_train)
        saver.save(sess, "./my_model_all_layers.ckpt")

Extracting /tmp/data/train-images-idx3-ubyte.gz
Extracting /tmp/data/train-labels-idx1-ubyte.gz
Extracting /tmp/data/t10k-images-idx3-ubyte.gz
Extracting /tmp/data/t10k-labels-idx1-ubyte.gz
0 Train MSE: 0.02705
1 Train MSE: 0.0137857
2 Train MSE: 0.0113694
3 Train MSE: 0.0107478

# utility: plot grayscale 28x28 image

def plot_image(image, shape=[28, 28]):
    plt.imshow(image.reshape(shape), cmap="Greys", interpolation="nearest")
    plt.axis("off")

# load model, eval on test set (measure reconstruction error, display original & reconstruction)

def show_reconstructed_digits(X, outputs, model_path = None, n_test_digits = 2):
    with tf.Session() as sess:
        if model_path:
            saver.restore(sess, model_path)
        X_test = mnist.test.images[:n_test_digits]
        outputs_val = outputs.eval(feed_dict={X: X_test})

    fig = plt.figure(figsize=(8, 3 * n_test_digits))
    for digit_index in range(n_test_digits):
        plt.subplot(n_test_digits, 2, digit_index * 2 + 1)
        plot_image(X_test[digit_index])
        plt.subplot(n_test_digits, 2, digit_index * 2 + 2)
        plot_image(outputs_val[digit_index])

show_reconstructed_digits(X, outputs, "./my_model_all_layers.ckpt")
plt.show()

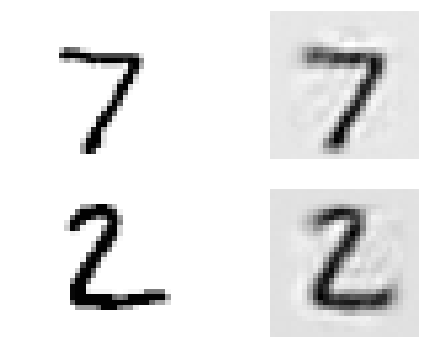
Tying Weights

Used when AE is symmetrical. Tying decoder layer weights to encoder layers' weights cuts number of weights by 50% (speedup & less memory).
Tied weights in TF is cumbersome. Easier to define layers manually.

tf.reset_default_graph()

activation = tf.nn.elu

regularizer = tf.contrib.layers.l2_regularizer(l2_reg)

initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])

weights1_init = initializer([n_inputs, n_hidden1])
weights2_init = initializer([n_hidden1, n_hidden2])

weights1 = tf.Variable(weights1_init, dtype=tf.float32, name="weights1")
weights2 = tf.Variable(weights2_init, dtype=tf.float32, name="weights2")
# weights 3,4 not vars!
weights3 = tf.transpose(weights2, name="weights3") # tied weights
weights4 = tf.transpose(weights1, name="weights4") # tied weights

biases1 = tf.Variable(tf.zeros(n_hidden1),name="biases1")
biases2 = tf.Variable(tf.zeros(n_hidden2),name="biases2")
biases3 = tf.Variable(tf.zeros(n_hidden3),name="biases3")
biases4 = tf.Variable(tf.zeros(n_outputs),name="biases4")

hidden1 = activation(tf.matmul(X, weights1) + biases1)
hidden2 = activation(tf.matmul(hidden1, weights2) + biases2)
hidden3 = activation(tf.matmul(hidden2, weights3) + biases3)
outputs = tf.matmul(hidden3, weights4) + biases4

reconstruction_loss = tf.reduce_mean(
    tf.square(outputs - X))

reg_loss = regularizer(weights1) + regularizer(weights2)

loss = reconstruction_loss + reg_loss

optimizer = tf.train.AdamOptimizer(learning_rate)

training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

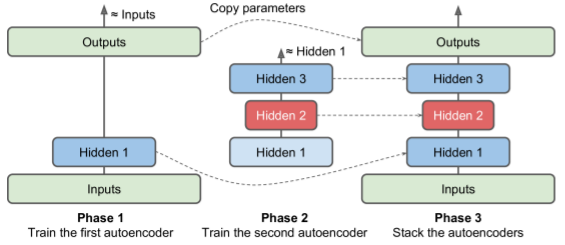
Training one Autoencoder at a time

Often faster to train each shallow AE individually, then stack them.
Simplest approach = use separate TF graph for each phase

def train_autoencoder(
    X_train, 
    n_neurons, 
    n_epochs, 
    batch_size, 
    learning_rate = 0.01, 
    l2_reg = 0.0005, 
    activation_fn=tf.nn.elu):

    graph = tf.Graph()
    with graph.as_default():
        n_inputs = X_train.shape[1]

        X = tf.placeholder(tf.float32, shape=[None, n_inputs])

        with tf.contrib.framework.arg_scope(
            [fully_connected],
            activation_fn=activation_fn,
            weights_initializer=tf.contrib.layers.variance_scaling_initializer(),
            weights_regularizer=tf.contrib.layers.l2_regularizer(
                l2_reg)):
            hidden = fully_connected(
                X, n_neurons, scope="hidden")
            outputs = fully_connected(
                hidden, n_inputs, activation_fn=None, scope="outputs")

        mse = tf.reduce_mean(tf.square(outputs - X))

        reg_losses = tf.get_collection(
            tf.GraphKeys.REGULARIZATION_LOSSES)

        loss = tf.add_n([mse] + reg_losses)

        optimizer = tf.train.AdamOptimizer(learning_rate)

        training_op = optimizer.minimize(loss)

        init = tf.global_variables_initializer()

    with tf.Session(graph=graph) as sess:
        init.run()

        for epoch in range(n_epochs):
            n_batches = len(X_train) // batch_size

            for iteration in range(n_batches):
                print("\r{}%".format(100 * iteration // n_batches), end="")
                sys.stdout.flush()

                indices = rnd.permutation(
                    len(X_train))[:batch_size]

                X_batch = X_train[indices]

                sess.run(
                    training_op, feed_dict={X: X_batch})

            mse_train = mse.eval(
                feed_dict={X: X_batch})

            print("\r{}".format(epoch), "Train MSE:", mse_train)

        params = dict(
            [(var.name, var.eval()) for var in tf.get_collection(
                tf.GraphKeys.TRAINABLE_VARIABLES)])

        hidden_val = hidden.eval(
            feed_dict={X: X_train})

        return hidden_val, params["hidden/weights:0"], params["hidden/biases:0"], params["outputs/weights:0"], params["outputs/biases:0"]

# train two AEs

hidden_output, W1, b1, W4, b4 = train_autoencoder(
    mnist.train.images, 
    n_neurons=300, 
    n_epochs=4, 
    batch_size=150)

_, W2, b2, W3, b3 = train_autoencoder(
    hidden_output, 
    n_neurons=150, 
    n_epochs=4, 
    batch_size=150)

0 Train MSE: 0.0193591
1 Train MSE: 0.0190697
2 Train MSE: 0.0188801
3 Train MSE: 0.0192353
0 Train MSE: 0.00428287
1 Train MSE: 0.00438113
2 Train MSE: 0.00464872
3 Train MSE: 0.00457076

# create stacked AE by reusing weights &and biases from above

tf.reset_default_graph()

n_inputs = 28*28

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden1 = tf.nn.elu(tf.matmul(X, W1) + b1)
hidden2 = tf.nn.elu(tf.matmul(hidden1, W2) + b2)
hidden3 = tf.nn.elu(tf.matmul(hidden2, W3) + b3)
outputs = tf.matmul(hidden3, W4) + b4

Visualizing Reconstructions

# Load model, evaluates it on test set (reconstruction error)
# display original & reconstructed images

def show_reconstructed_digits(
    X, 
    outputs, 
    model_path = None, 
    n_test_digits = 2):

    with tf.Session() as sess:
        if model_path:
            saver.restore(sess, model_path)

        X_test = mnist.test.images[:n_test_digits]
        outputs_val = outputs.eval(feed_dict={X: X_test})

    fig = plt.figure(figsize=(8, 3 * n_test_digits))

    for digit_index in range(n_test_digits):

        plt.subplot(n_test_digits, 2, digit_index * 2 + 1)
        plot_image(X_test[digit_index])
        plt.subplot(n_test_digits, 2, digit_index * 2 + 2)
        plot_image(outputs_val[digit_index])
        plt.show()

#show_reconstructed_digits(X, outputs, "./my_model_all_layers.ckpt")
show_reconstructed_digits(X, outputs)

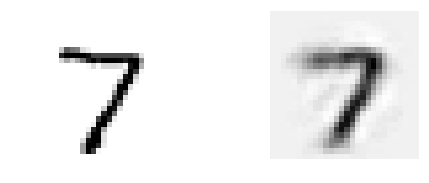
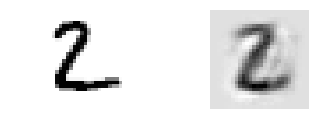
Visualizing Features

simplest method: find training instances that activate each hidden node the most. (best on upper layers, given their tendency to capture high-level features.)

ch15 autoencoders.md

Data Representations

PCA with Undercomplete Linear Autoencoder

Stacked Autoencoders

Tying Weights

Training one Autoencoder at a time

Visualizing Reconstructions

Visualizing Features

Unsupervised Pretraining with Stacked Autoencoders

Denoising Autoencoders

Sparse Autoencoders

Variational Autoencoders

Other Autoencoders

results matching ""

No results matching ""