Gaussian process regrssion demo

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline  
print ("Packages Loaded")

Packages Loaded

Define training data

x = np.array([[1, 2, 3, 4, 6, 7, 9, 10]]).T
y = np.array([[2, 4, 5, 1, 3, 9, 11, 5]]).T

# Plot
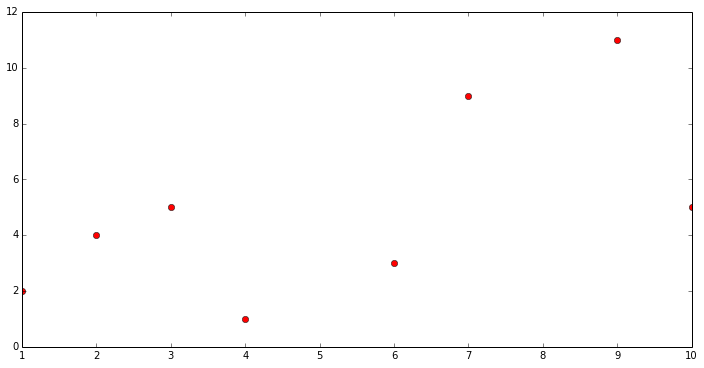
plt.figure(1, figsize=(12, 6))
plt.plot(x[:, 0], y[:, 0], 'ro', label='Original data')

print ("Training data")

Training data

Define kernel function

def kernel_se(X1, X2):
    n1 = X1.shape[0]
    n2 = X2.shape[0]
    K  = np.zeros((n1, n2))
    for i in range(n1):
        for j in range(n2):
            x1 = X1[i, :]
            x2 = X2[j, :]
            d  = x1 - x2
            K[i, j] = 10*np.exp(-d*d/(10))
            if n1 > 1 and i == j:
                K[i, j] = K[i, j] + 0.001
    return K
print ("Define kernel function")

Define kernel function

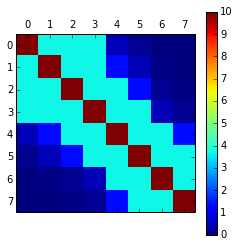
Kernel matrix

K = kernel_se(x, x)
plt.figure(1, figsize=(6, 6))
plt.matshow(K)
plt.colorbar()
plt.show()

<matplotlib.figure.Figure at 0x7f7f8d958f50>


/usr/lib/pymodules/python2.7/matplotlib/collections.py:548: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison
  if self._edgecolors == 'face':

Do Gaussian process regression

ntest = 100
xtest = np.array([np.linspace(0, 10, ntest)]).T
Ktest = kernel_se(xtest, x)

# GPR
alpha = np.matmul(np.linalg.inv(K), y)
ytest = np.matmul(Ktest, alpha)
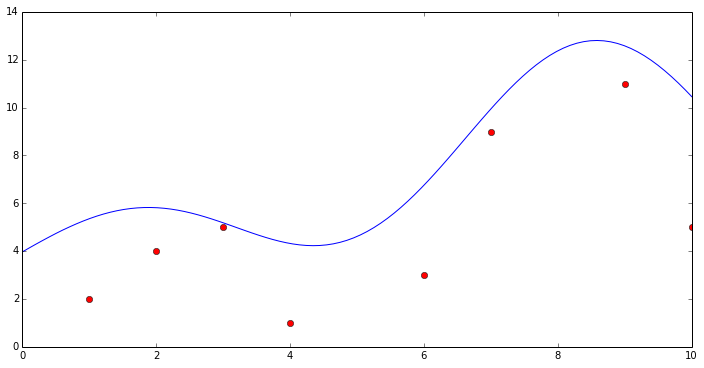
plt.figure(1, figsize=(12, 6))
plt.plot(x[:, 0], y[:, 0], 'ro', label='Original data')
plt.plot(xtest[:, 0], ytest[:, 0], 'b-', label='GPR')

[<matplotlib.lines.Line2D at 0x7f7f8db4c550>]

GP Variance

vartest = np.zeros((ntest, 1))
for i in range(ntest):
    xtemp  = xtest[i:i+1, :]
    ktemp  = kernel_se(xtemp, xtemp)
    ktemp2 = kernel_se(xtemp, x)
    Mtemp  = np.matmul(ktemp2, np.linalg.inv(K))
    Mtemp2 = np.matmul(Mtemp, ktemp2.T)
    vartest[i, :] = ktemp - Mtemp2

# Plot
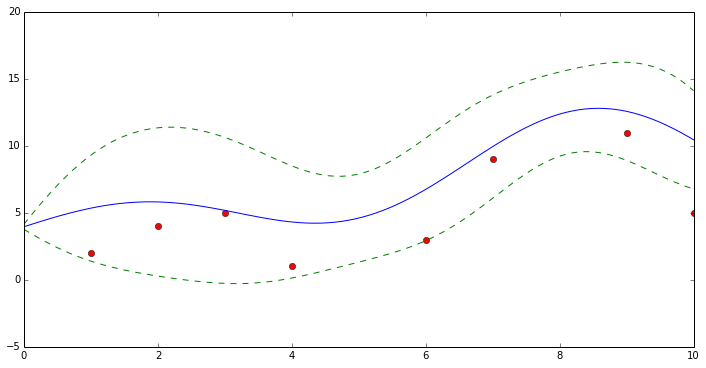
plt.figure(1, figsize=(12, 6))
plt.plot(x[:, 0], y[:, 0], 'ro', label='Original data')
plt.plot(xtest[:, 0], ytest[:, 0], 'b-', label='GPR')
plt.plot(xtest[:, 0], ytest[:, 0] + vartest[:, 0], 'g--', label='GPR')
plt.plot(xtest[:, 0], ytest[:, 0] - vartest[:, 0], 'g--', label='GPR')

[<matplotlib.lines.Line2D at 0x7f7f8d968a10>]