Market Competitiveness
来一个奇葩无厘头的市场竞争策略
策略思路
某一行业的几大龙头股票,在稳定时期此消彼长
策略实现
股票池:选择一行业内的流动性比较好的龙头股票;例如三家自助品牌汽车,长安、比亚迪和长城,以下按照三只股票情况讨论
观察某一天时,股票价格和该股票在过去几天内平均值的关系
如果两只股票下跌,则预测另一只股票上涨;如果两只股票上涨,则预测另一只股票下跌
如果某天三只股票中的两只较其平均值有较大幅度下跌,而另一只股票较其平均值比较稳定不变,则买入后面这只比较稳定的股票
如果某天三只股票中的两只较其平均值有较大幅度上涨,而另一只股票较其平均值比较稳定不变,则卖出后面这只比较稳定的股票
import quartz
import quartz.backtest as qb
import quartz.performance as qp
from quartz.api import *
import pandas as pd
import numpy as np
from datetime import datetime
from matplotlib import pylab
start = datetime(2012, 1, 1)
end = datetime(2014, 12, 1)
benchmark = 'HS300'
universe = ['000625.XSHE', # 长安汽车
'002594.XSHE', # 比亚迪汽车
'601633.XSHG' # 长城汽车
]
capital_base = 1000000
refresh_rate = 5
window = 10
def initialize(account):
account.amount = 100000
account.universe = universe
add_history('hist', window)
def handle_data(account):
stk_0 = universe[0]
stk_1 = universe[1]
stk_2 = universe[2]
prices_0 = account.hist[stk_0]['closePrice']
prices_1 = account.hist[stk_1]['closePrice']
prices_2 = account.hist[stk_2]['closePrice']
mu_0 = prices_0.mean()
mu_1 = prices_1.mean()
mu_2 = prices_2.mean()
# 两只下跌较大幅度,一只较稳定,买入较稳定这只股票
if prices_0[-1] > mu_0 and prices_1[-1] < 0.975 * mu_1 and prices_2[-1] < 0.975 * mu_2:
order(stk_0, account.amount)
if prices_1[-1] > mu_1 and prices_2[-1] < 0.975 * mu_2 and prices_0[-1] < 0.975 * mu_0:
order(stk_1, account.amount)
if prices_2[-1] > mu_2 and prices_0[-1] < 0.975 * mu_0 and prices_1[-1] < 0.975 * mu_1:
order(stk_2, account.amount)
# 两只上涨较大幅度,一只较稳定,卖出较稳定这只股票
if prices_0[-1] < mu_0 and prices_1[-1] > 1.025 * mu_1 and prices_2[-1] > 1.025 * mu_2:
order_to(stk_0, 0)
if prices_1[-1] < mu_1 and prices_0[-1] > 1.025 * mu_0 and prices_2[-1] > 1.025 * mu_2:
order_to(stk_1, 0)
if prices_2[-1] < mu_2 and prices_0[-1] > 1.025 * mu_0 and prices_1[-1] > 1.025 * mu_1:
order_to(stk_2, 0)
bt
| tradeDate | cash | stock_position | portfolio_value | benchmark_return | blotter | |
|---|---|---|---|---|---|---|
| 0 | 2012-01-18 | 1000000.00000 | {} | 1000000.00000 | 0.000000 | [] |
| 1 | 2012-01-19 | 1000000.00000 | {} | 1000000.00000 | 0.019058 | [] |
| 2 | 2012-01-20 | 1000000.00000 | {} | 1000000.00000 | 0.014478 | [] |
| 3 | 2012-01-30 | 1000000.00000 | {} | 1000000.00000 | -0.017318 | [] |
| 4 | 2012-01-31 | 1000000.00000 | {} | 1000000.00000 | 0.001439 | [] |
| 5 | 2012-02-01 | 1000000.00000 | {} | 1000000.00000 | -0.014311 | [] |
| 6 | 2012-02-02 | 1000000.00000 | {} | 1000000.00000 | 0.023567 | [] |
| 7 | 2012-02-03 | 1000000.00000 | {} | 1000000.00000 | 0.007985 | [] |
| 8 | 2012-02-06 | 1000000.00000 | {} | 1000000.00000 | -0.000705 | [] |
| 9 | 2012-02-07 | 1000000.00000 | {} | 1000000.00000 | -0.018515 | [] |
| 10 | 2012-02-08 | 1000000.00000 | {} | 1000000.00000 | 0.028594 | [] |
| 11 | 2012-02-09 | 1000000.00000 | {} | 1000000.00000 | 0.000394 | [] |
| 12 | 2012-02-10 | 1000000.00000 | {} | 1000000.00000 | 0.001737 | [] |
| 13 | 2012-02-13 | 1000000.00000 | {} | 1000000.00000 | -0.000648 | [] |
| 14 | 2012-02-14 | 1000000.00000 | {} | 1000000.00000 | -0.003900 | [] |
| 15 | 2012-02-15 | 1000000.00000 | {} | 1000000.00000 | 0.010904 | [] |
| 16 | 2012-02-16 | 1000000.00000 | {} | 1000000.00000 | -0.005308 | [] |
| 17 | 2012-02-17 | 1000000.00000 | {} | 1000000.00000 | 0.000399 | [] |
| 18 | 2012-02-20 | 1000000.00000 | {} | 1000000.00000 | 0.001427 | [] |
| 19 | 2012-02-21 | 1000000.00000 | {} | 1000000.00000 | 0.008559 | [] |
| 20 | 2012-02-22 | 1000000.00000 | {} | 1000000.00000 | 0.013668 | [] |
| 21 | 2012-02-23 | 1000000.00000 | {} | 1000000.00000 | 0.003380 | [] |
| 22 | 2012-02-24 | 1000000.00000 | {} | 1000000.00000 | 0.016023 | [] |
| 23 | 2012-02-27 | 1000000.00000 | {} | 1000000.00000 | 0.003231 | [] |
| 24 | 2012-02-28 | 1000000.00000 | {} | 1000000.00000 | 0.002217 | [] |
| 25 | 2012-02-29 | 1000000.00000 | {} | 1000000.00000 | -0.010637 | [] |
| 26 | 2012-03-01 | 1000000.00000 | {} | 1000000.00000 | -0.000303 | [] |
| 27 | 2012-03-02 | 1000000.00000 | {} | 1000000.00000 | 0.017692 | [] |
| 28 | 2012-03-05 | 1000000.00000 | {} | 1000000.00000 | -0.006432 | [] |
| 29 | 2012-03-06 | 1000000.00000 | {} | 1000000.00000 | -0.015641 | [] |
| ... | ... | ... | ... | ... | ... | ... |
| 664 | 2014-10-21 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1913031.23401 | -0.008685 | [] |
| 665 | 2014-10-22 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1933648.47401 | -0.006062 | [] |
| 666 | 2014-10-23 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1953640.67401 | -0.009385 | [] |
| 667 | 2014-10-24 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1823065.79401 | -0.002183 | [] |
| 668 | 2014-10-27 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1859302.04401 | -0.009152 | [] |
| 669 | 2014-10-28 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1863675.44401 | 0.020187 | [] |
| 670 | 2014-10-29 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1871797.24401 | 0.014371 | [] |
| 671 | 2014-10-30 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1883042.97401 | 0.007156 | [] |
| 672 | 2014-10-31 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1913656.09401 | 0.015958 | [] |
| 673 | 2014-11-03 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1902410.64401 | 0.001682 | [] |
| 674 | 2014-11-04 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1964886.42401 | 0.000247 | [] |
| 675 | 2014-11-05 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2049228.79401 | -0.003869 | [] |
| 676 | 2014-11-06 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2020489.70401 | 0.001047 | [] |
| 677 | 2014-11-07 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2027362.02401 | -0.001564 | [] |
| 678 | 2014-11-10 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2043606.06401 | 0.025410 | [] |
| 679 | 2014-11-11 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2022988.64401 | -0.002775 | [] |
| 680 | 2014-11-12 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2049228.91401 | 0.013957 | [] |
| 681 | 2014-11-13 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2054226.61401 | -0.005616 | [] |
| 682 | 2014-11-14 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1987377.18401 | 0.000519 | [] |
| 683 | 2014-11-17 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1988626.85401 | -0.005420 | [] |
| 684 | 2014-11-18 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2006744.97401 | -0.010004 | [] |
| 685 | 2014-11-19 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2014241.95401 | -0.001653 | [] |
| 686 | 2014-11-20 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1980504.81401 | -0.000047 | [] |
| 687 | 2014-11-21 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 1989251.55401 | 0.018273 | [] |
| 688 | 2014-11-24 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2085464.99401 | 0.025470 | [] |
| 689 | 2014-11-25 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2156687.78401 | 0.013702 | [] |
| 690 | 2014-11-26 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2142942.92401 | 0.013949 | [] |
| 691 | 2014-11-27 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2146691.26401 | 0.011557 | [] |
| 692 | 2014-11-28 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2276016.94401 | 0.019724 | [] |
| 693 | 2014-12-01 | 1.56401 | {u'000625.XSHE': 1.0, u'601633.XSHG': 62476.0} | 2245404.03401 | 0.003913 | [] |
694 rows × 6 columns
perf = qp.perf_parse(bt)
out_keys = ['annualized_return', 'volatility', 'information',
'sharpe', 'max_drawdown', 'alpha', 'beta']
for k in out_keys:
print '%s: %s' % (k, perf[k])
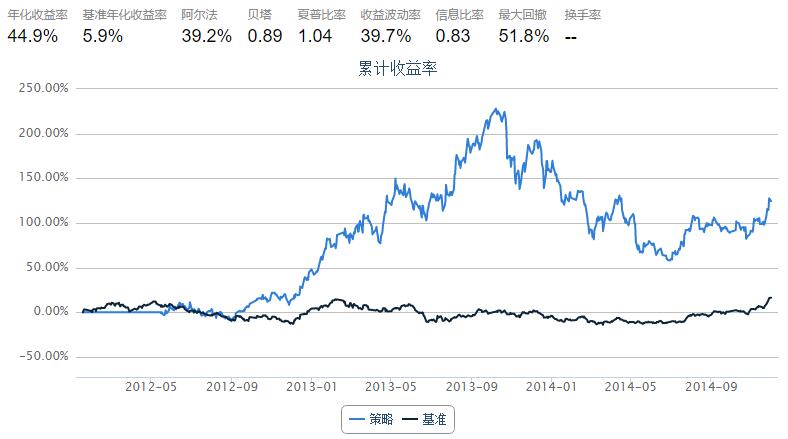
annualized_return: 0.448632577093
volatility: 0.397466535866
information: 0.825863671828
sharpe: 1.04326663926
max_drawdown: 0.518092986656
alpha: 0.392363999248
beta: 0.886220585368
perf['cumulative_return'].plot()
perf['benchmark_cumulative_return'].plot()
pylab.legend(['current_strategy','HS300'])
<matplotlib.legend.Legend at 0x4e27c50>
