实现损失函数
损失函数对于机器学习算法非常重要。它们测量模型输出与目标(真值)值之间的距离。在这个秘籍中,我们在 TensorFlow 中展示了各种损失函数实现。
做好准备
为了优化我们的机器学习算法,我们需要评估结果。评估 TensorFlow 中的结果取决于指定损失函数。损失函数告诉 TensorFlow 预测与期望结果相比有多好或多坏。在大多数情况下,我们将有一组数据和一个目标来训练我们的算法。损失函数将目标与预测进行比较,并给出两者之间的数值距离。
对于这个秘籍,我们将介绍我们可以在 TensorFlow 中实现的主要损失函数。
要了解不同损失函数的运行方式,我们将在此秘籍中绘制它们。我们将首先启动一个计算图并加载matplotlib,一个 Python 绘图库,如下所示:
import matplotlib.pyplot as plt
import tensorflow as tf
操作步骤
- 首先,我们将讨论回归的损失函数,这意味着预测连续的因变量。首先,我们将创建一个预测序列和一个作为张量的目标。我们将在-1 和 1 之间输出 500 x 值的结果。有关输出的绘图,请参阅“工作原理...”部分。使用以下代码:
x_vals = tf.linspace(-1., 1., 500)
target = tf.constant(0.)
- L2 范数损失也称为欧几里德损失函数。它只是到目标的距离的平方。在这里,我们将计算损失函数,就像目标为零一样。 L2 范数是一个很大的损失函数,因为它在目标附近非常弯曲,并且算法可以使用这个事实来越慢地收敛到目标,越接近零。我们可以按如下方式实现:
l2_y_vals = tf.square(target - x_vals)
l2_y_out = sess.run(l2_y_vals)
TensorFlow 具有 L2 范数的内置形式,称为
nn.l2_loss()。这个函数实际上是 L2 规范的一半。换句话说,它与前一个相同,但除以 2。
- L1 范数损失也称为绝对损失函数。我们不是平衡差异,而是取绝对值。 L1 范数对于异常值比 L2 范数更好,因为对于较大的值,它不是那么陡峭。需要注意的一个问题是 L1 范数在目标处不平滑,这可能导致算法收敛不好。它看起来如下:
l1_y_vals = tf.abs(target - x_vals)
l1_y_out = sess.run(l1_y_vals)
- 伪 Huber 损失是 Huber 损失函数的连续且平滑的近似。这种损失函数试图通过在目标附近凸起并且对于极值不太陡峭来充分利用 L1 和 L2 范数。表格取决于额外的参数 delta,它决定了它的陡峭程度。我们将绘制两种形式,
delta1 = 0.25和delta2 = 5,以显示差异,如下所示:
delta1 = tf.constant(0.25)
phuber1_y_vals = tf.multiply(tf.square(delta1), tf.sqrt(1\. +
tf.square((target - x_vals)/delta1)) - 1.)
phuber1_y_out = sess.run(phuber1_y_vals)
delta2 = tf.constant(5.)
phuber2_y_vals = tf.multiply(tf.square(delta2), tf.sqrt(1\. +
tf.square((target - x_vals)/delta2)) - 1.)
phuber2_y_out = sess.run(phuber2_y_vals)
现在,我们继续讨论分类问题的损失函数。分类损失函数用于在预测分类结果时评估损失。通常,我们的类别类型的输出是 0 到 1 之间的实数值。然后,我们选择截止值(通常选择 0.5)并且如果数字高于截止值,则将结果分类为该类别。在这里,我们考虑分类输出的各种损失函数:
- 首先,我们需要重新定义我们的预测(
x_vals)和target。我们将保存输出并在下一节中绘制它们。使用以下内容:
x_vals = tf.linspace(-3., 5., 500)
target = tf.constant(1.)
targets = tf.fill([500,], 1.)
- 铰链损失主要用于支持向量机,但也可用于神经网络。它旨在计算两个目标类 1 和-1 之间的损失。在下面的代码中,我们使用目标值
1,因此我们的预测越接近 1,损失值越低:
hinge_y_vals = tf.maximum(0., 1\. - tf.multiply(target, x_vals))
hinge_y_out = sess.run(hinge_y_vals)
- 二元情形的交叉熵损失有时也称为逻辑损失函数。它是在我们预测两个 0 或 1 类时出现的。我们希望测量从实际类(0 或 1)到预测值的距离,预测值通常是介于 0 和 1 之间的实数。为了测量这个距离,我们可以使用信息论中的交叉熵公式,如下:
xentropy_y_vals = - tf.multiply(target, tf.log(x_vals)) - tf.multiply((1\. - target), tf.log(1\. - x_vals))
xentropy_y_out = sess.run(xentropy_y_vals)
- Sigmoid 交叉熵损失与之前的损失函数非常相似,除了我们在将它们置于交叉熵损失之前使用 sigmoid 函数转换 x 值,如下所示:
xentropy_sigmoid_y_vals = tf.nn.sigmoid_cross_entropy_with_logits_v2(logits=x_vals, labels=targets)
xentropy_sigmoid_y_out = sess.run(xentropy_sigmoid_y_vals)
- 加权交叉熵损失是 S 形交叉熵损失的加权版本。我们对积极目标给予了重视。举个例子,我们将正面目标加权 0.5,如下:
weight = tf.constant(0.5)
xentropy_weighted_y_vals = tf.nn.weighted_cross_entropy_with_logits(logits=x_vals, targets=targets, pos_weight=weight)
xentropy_weighted_y_out = sess.run(xentropy_weighted_y_vals)
- Softmax 交叉熵损失在非标准化输出上运行。当只有一个目标类别而不是多个目标类别时,此函数用于测量损失。因此,函数通过 softmax 函数将输出转换为概率分布,然后根据真实概率分布计算损失函数,如下所示:
unscaled_logits = tf.constant([[1., -3., 10.]])
target_dist = tf.constant([[0.1, 0.02, 0.88]])
softmax_xentropy = tf.nn.softmax_cross_entropy_with_logits_v2(logits=unscaled_logits, labels=target_dist)
print(sess.run(softmax_xentropy))
[ 1.16012561]
- 稀疏 softmax 交叉熵损失与前一个相同,除了目标是概率分布,它是哪个类别为真的索引。我们只传递真值的类别的索引,而不是稀疏的全零目标向量,其值为 1,如下所示:
unscaled_logits = tf.constant([[1., -3., 10.]])
sparse_target_dist = tf.constant([2])
sparse_xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=unscaled_logits, labels=sparse_target_dist)
print(sess.run(sparse_xentropy))
[ 0.00012564]
工作原理
以下是如何使用matplotlib绘制回归损失函数:
x_array = sess.run(x_vals)
plt.plot(x_array, l2_y_out, 'b-', label='L2 Loss')
plt.plot(x_array, l1_y_out, 'r--', label='L1 Loss')
plt.plot(x_array, phuber1_y_out, 'k-.', label='P-Huber Loss (0.25)')
plt.plot(x_array, phuber2_y_out, 'g:', label='P-Huber Loss (5.0)')
plt.ylim(-0.2, 0.4)
plt.legend(loc='lower right', prop={'size': 11})
plt.show()
我们得到以下图作为上述代码的输出:
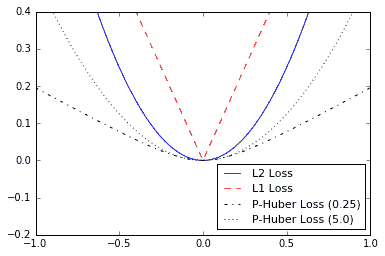
图 4:绘制各种回归损失函数
以下是如何使用matplotlib绘制各种分类损失函数:
x_array = sess.run(x_vals)
plt.plot(x_array, hinge_y_out, 'b-''', label='Hinge Loss''')
plt.plot(x_array, xentropy_y_out, 'r--''', label='Cross' Entropy Loss')
plt.plot(x_array, xentropy_sigmoid_y_out, 'k-.''', label='Cross' Entropy Sigmoid Loss')
plt.plot(x_array, xentropy_weighted_y_out, g:''', label='Weighted' Cross Enropy Loss (x0.5)')
plt.ylim(-1.5, 3)
plt.legend(loc='lower right''', prop={'size''': 11})
plt.show()
我们从前面的代码中得到以下图:
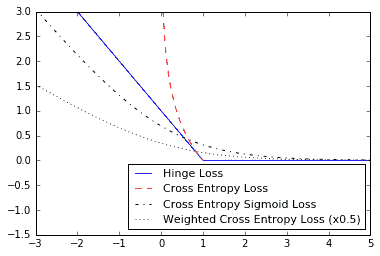 Figure 5: Plots of classification loss functions
Figure 5: Plots of classification loss functions
更多
这是一个总结我们描述的不同损失函数的表:
| 损失函数 | 任务 | 优点 | 缺点 |
|---|---|---|---|
| L2 | 回归 | 更稳定 | 不太健壮 |
| L1 | 回归 | 更强大 | 不太稳定 |
| 伪胡伯 | 回归 | 更稳健,更稳定 | 还有一个参数 |
| 合页 | 分类 | 创建 SVM 中使用的最大边距 | 受到异常值影响的无限损失 |
| 交叉熵 | 分类 | 更稳定 | 无限损失,不那么强大 |
剩余的分类损失函数都与交叉熵损失的类型有关。交叉熵 sigmoid los 函数用于未缩放的 logits,并且优于计算 sigmoid 然后交叉熵,因为 TensorFlow 具有更好的内置方式来处理数字边缘情况。 softmax 交叉熵和稀疏 softmax 交叉熵也是如此。
这里描述的大多数分类损失函数用于两类预测。通过对每个预测/目标上的交叉熵项求和,可以将其扩展到多个类。
评估模型时还需要考虑许多其他指标。以下列出了一些需要考虑的事项:
| 模型指标 | 描述 |
|---|---|
| R 平方(确定系数) | 对于线性模型,这是因变量的方差比例,由独立数据解释。对于具有大量特征的模型,请考虑使用调整后的 R 平方。 |
| 均方根误差 | 对于连续模型,它通过平均平方误差的平方根来测量预测与实际之间的差异。 |
| 混淆矩阵 | 对于分类模型,我们查看预测类别与实际类别的矩阵。一个完美的模型具有沿对角线的所有计数。 |
| 召回 | 对于分类模型,这是所有预测阳性的真阳性分数。 |
| 精确 | 对于分类模型,这是所有实际正数的真实积极分数。 |
| F-得分 | 对于分类模型,这是精度和召回的调和平均值。 |