学习玩井字棋

为了展示适应性神经网络的可用性，我们现在将尝试使用神经网络来学习井字棋的最佳动作。我们将知道井字棋是一种确定性游戏，并且最佳动作已经知道。

做好准备

为了训练我们的模型，我们将使用一系列的棋盘位置，然后对许多不同的棋盘进行最佳的最佳响应。我们可以通过仅考虑在对称性方面不同的棋盘位置来减少要训练的棋盘数量。井字棋棋盘的非同一性变换是 90 度，180 度和 270 度的旋转（在任一方向上），水平反射和垂直反射。鉴于这个想法，我们将使用最佳移动的候选棋盘名单，应用两个随机变换，然后将其输入神经网络进行学习。

由于井字棋是一个确定性的游戏，值得注意的是，无论谁先走，都应该赢或抽。我们希望能够以最佳方式响应我们的动作并最终获得平局的模型。

如果我们将 Xs 注释为 1，将 Os 注释为-1，将空格注释为 0，则下图说明了我们如何将棋盘位置和最佳移动视为一行数据：

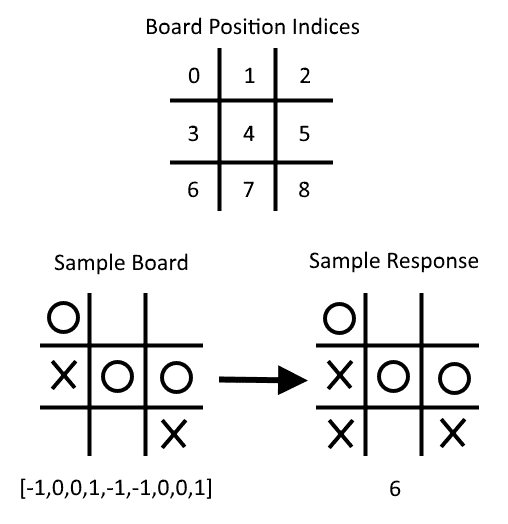Figure 9: Here, we illustrate how to consider a board and an optimal move as a row of data. Note that X = 1, O = -1, and empty spaces are 0, and we start indexing at 0

除了模型损失，要检查我们的模型如何执行，我们将做两件事。我们将执行的第一项检查是从训练集中删除位置和最佳移动行。这将使我们能够看到神经网络模型是否可以推广它以前从未见过的移动。我们将评估模型的第二种方法是在最后实际对抗它。

可以在此秘籍的 GitHub 目录中找到可能的棋盘列表和最佳移动： https://github.com/nfmcclure/tensorflow_cookbook/tree/master/06_Neural_Networks/08_Learning_Tic_Tac_Toe 和 Packt 仓库： https://github.com/PacktPublishing/TensorFlow-Machine-Learning-Cookbook-Second-Edition 。

操作步骤

我们按如下方式处理秘籍：

1. 我们需要从为此脚本加载必要的库开始，如下所示：

import tensorflow as tf 
import matplotlib.pyplot as plt 
import csv 
import random 
import numpy as np 
import random

1. 接下来，我们声明以下批量大小来训练我们的模型：

batch_size = 50

1. 为了使棋盘更容易可视化，我们将创建一个输出带 Xs 和 Os 的井字棋棋盘的函数。这是通过以下代码完成的：

 def print_board(board):
    symbols = ['O', ' ', 'X']
    board_plus1 = [int(x) + 1 for x in board]
    board_line1 = ' {} | {} | {}'.format(symbols[board_plus1[0]],
                                         symbols[board_plus1[1]],
                                         symbols[board_plus1[2]])
    board_line2 = ' {} | {} | {}'.format(symbols[board_plus1[3]],
                                         symbols[board_plus1[4]],
                                         symbols[board_plus1[5]])
    board_line3 = ' {} | {} | {}'.format(symbols[board_plus1[6]],
                                         symbols[board_plus1[7]],
                                         symbols[board_plus1[8]])
    print(board_line1)
    print('___________')
    print(board_line2)
    print('___________')
    print(board_line3)

1. 现在我们必须创建一个函数，它将返回一个新的棋盘和一个转换下的最佳响应位置。这是通过以下代码完成的：

def get_symmetry(board, response, transformation): 
    ''' 
    :param board: list of integers 9 long: 
     opposing mark = -1 
     friendly mark = 1 
     empty space = 0 
    :param transformation: one of five transformations on a board: 
     rotate180, rotate90, rotate270, flip_v, flip_h 
    :return: tuple: (new_board, new_response) 
    ''' 

    if transformation == 'rotate180': 
        new_response = 8 - response 
        return board[::-1], new_response 

    elif transformation == 'rotate90': 
        new_response = [6, 3, 0, 7, 4, 1, 8, 5, 2].index(response) 
        tuple_board = list(zip(*[board[6:9], board[3:6], board[0:3]])) 
        return [value for item in tuple_board for value in item], new_response 

    elif transformation == 'rotate270': 
        new_response = [2, 5, 8, 1, 4, 7, 0, 3, 6].index(response) 
        tuple_board = list(zip(*[board[0:3], board[3:6], board[6:9]]))[::-1] 
        return [value for item in tuple_board for value in item], new_response 

    elif transformation == 'flip_v': 
        new_response = [6, 7, 8, 3, 4, 5, 0, 1, 2].index(response) 
        return board[6:9] +  board[3:6] + board[0:3], new_response 

    elif transformation == 'flip_h': 
    # flip_h = rotate180, then flip_v 
        new_response = [2, 1, 0, 5, 4, 3, 8, 7, 6].index(response) 
        new_board = board[::-1] 
        return new_board[6:9] +  new_board[3:6] + new_board[0:3], new_response 

    else: 
        raise ValueError('Method not implmented.')

1. 棋盘列表及其最佳响应位于目录中的.csv文件中，可从 github 仓库 https://github.com/nfmcclure/tensorflow_cookbook 或 Packt 仓库获得 https://github.com/PacktPublishing/TensorFlow-Machine-Learning-Cookbook-Second-Edition。我们将创建一个函数，它将使用棋盘和响应加载文件，并将其存储为元组列表，如下所示：

def get_moves_from_csv(csv_file): 
    ''' 
    :param csv_file: csv file location containing the boards w/ responses 
    :return: moves: list of moves with index of best response 
    ''' 
    moves = [] 
    with open(csv_file, 'rt') as csvfile: 
        reader = csv.reader(csvfile, delimiter=',') 
        for row in reader: 
            moves.append(([int(x) for x in row[0:9]],int(row[9]))) 
    return moves

1. 现在我们需要将所有内容组合在一起以创建一个函数，该函数将返回随机转换的棋盘和响应。这是通过以下代码完成的：

def get_rand_move(moves, rand_transforms=2): 
    # This function performs random transformations on a board. 
    (board, response) = random.choice(moves) 
    possible_transforms = ['rotate90', 'rotate180', 'rotate270', 'flip_v', 'flip_h'] 
    for i in range(rand_transforms): 
        random_transform = random.choice(possible_transforms) 
        (board, response) = get_symmetry(board, response, random_transform) 
    return board, response

1. 接下来，我们需要初始化图会话，加载数据，并创建一个训练集，如下所示：

sess = tf.Session() 
moves = get_moves_from_csv('base_tic_tac_toe_moves.csv') 
# Create a train set: 
train_length = 500 
train_set = [] 
for t in range(train_length): 
    train_set.append(get_rand_move(moves))

1. 请记住，我们希望从我们的训练集中删除一个棋盘和一个最佳响应，以查看该模型是否可以推广以实现最佳移动。以下棋盘的最佳举措将是在第 6 号指数进行：

test_board = [-1, 0, 0, 1, -1, -1, 0, 0, 1] 
train_set = [x for x in train_set if x[0] != test_board]

1. 我们现在可以创建函数来创建模型变量和模型操作。请注意，我们在以下模型中不包含softmax()激活函数，因为它包含在损失函数中：

def init_weights(shape): 
    return tf.Variable(tf.random_normal(shape)) 

def model(X, A1, A2, bias1, bias2): 
    layer1 = tf.nn.sigmoid(tf.add(tf.matmul(X, A1), bias1)) 
    layer2 = tf.add(tf.matmul(layer1, A2), bias2) 
    return layer2

1. 现在我们需要声明我们的占位符，变量和模型，如下所示：

X = tf.placeholder(dtype=tf.float32, shape=[None, 9]) 
Y = tf.placeholder(dtype=tf.int32, shape=[None]) 
A1 = init_weights([9, 81]) 
bias1 = init_weights([81]) 
A2 = init_weights([81, 9]) 
bias2 = init_weights([9]) 
model_output = model(X, A1, A2, bias1, bias2)

1. 接下来，我们需要声明我们的loss函数，它将是最终输出 logits 的平均 softmax（非标准化输出）。然后我们将声明我们的训练步骤和优化器。如果我们希望将来能够对抗我们的模型，我们还需要创建一个预测操作，如下所示：

loss = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(logits=model_output, labels=Y)) 
train_step = tf.train.GradientDescentOptimizer(0.025).minimize(loss) 
prediction = tf.argmax(model_output, 1)

1. 我们现在可以使用以下代码初始化变量并循环遍历神经网络的训练：

# Initialize variables 
init = tf.global_variables_initializer() 
sess.run(init) 
loss_vec = [] 
for i in range(10000): 
    # Select random indices for batch 
    rand_indices = np.random.choice(range(len(train_set)), batch_size, replace=False) 
    # Get batch 
    batch_data = [train_set[i] for i in rand_indices] 
    x_input = [x[0] for x in batch_data] 
    y_target = np.array([y[1] for y in batch_data]) 
    # Run training step 
    sess.run(train_step, feed_dict={X: x_input, Y: y_target}) 
    # Get training loss 
    temp_loss = sess.run(loss, feed_dict={X: x_input, Y: y_target}) 
    loss_vec.append(temp_loss)

    if i%500==0: 
        print('iteration ' + str(i) + ' Loss: ' + str(temp_loss))

1. 以下是绘制模型训练损失所需的代码：

plt.plot(loss_vec, 'k-', label='Loss') 
plt.title('Loss (MSE) per Generation') 
plt.xlabel('Generation') 
plt.ylabel('Loss') 
plt.show()

我们应该得到以下每代损失的绘图：

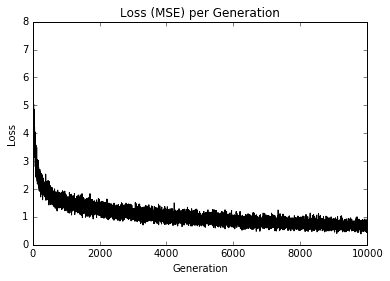
图 10：Tic-Tac-Toe 训练组损失超过 10,000 次迭代

在上图中，我们绘制了训练步骤的损失。

1. 为了测试模型，我们需要看看它是如何在我们从训练集中删除的测试棋盘上执行的。我们希望模型可以推广和预测移动的最佳索引，这将是索引号 6.大多数时候模型将成功，如下所示：

test_boards = [test_board] 
feed_dict = {X: test_boards} 
logits = sess.run(model_output, feed_dict=feed_dict) 
predictions = sess.run(prediction, feed_dict=feed_dict) 
print(predictions)

1. 上一步应该产生以下输出：

[6]

1. 为了评估我们的模型，我们需要与我们训练的模型进行对比。要做到这一点，我们必须创建一个能够检查胜利的函数。这样，我们的程序将知道何时停止要求更多动作。这是通过以下代码完成的：

def check(board): 
    wins = [[0,1,2], [3,4,5], [6,7,8], [0,3,6], [1,4,7], [2,5,8], [0,4,8], [2,4,6]] 
    for i in range(len(wins)): 
        if board[wins[i][0]]==board[wins[i][1]]==board[wins[i][2]]==1.: 
            return 1 
        elif board[wins[i][0]]==board[wins[i][1]]==board[wins[i][2]]==-1.: 
            return 1 
    return 0

1. 现在我们可以使用我们的模型循环播放游戏。我们从一个空白棋盘（全零）开始，我们要求用户输入一个索引（0-8），然后我们将其输入到模型中进行预测。对于模型的移动，我们采用最大的可用预测，也是一个开放空间。从这个游戏中，我们可以看到我们的模型并不完美，如下所示：

game_tracker = [0., 0., 0., 0., 0., 0., 0., 0., 0.] 
win_logical = False 
num_moves = 0 
while not win_logical: 
    player_index = input('Input index of your move (0-8): ') 
    num_moves += 1 
    # Add player move to game 
    game_tracker[int(player_index)] = 1\. 

    # Get model's move by first getting all the logits for each index 
    [potential_moves] = sess.run(model_output, feed_dict={X: [game_tracker]}) 
    # Now find allowed moves (where game tracker values = 0.0) 
    allowed_moves = [ix for ix,x in enumerate(game_tracker) if x==0.0] 
    # Find best move by taking argmax of logits if they are in allowed moves 
    model_move = np.argmax([x if ix in allowed_moves else -999.0 for ix,x in enumerate(potential_moves)]) 

    # Add model move to game 
    game_tracker[int(model_move)] = -1\. 
    print('Model has moved') 
    print_board(game_tracker) 
    # Now check for win or too many moves 
    if check(game_tracker)==1 or num_moves>=5: 
        print('Game Over!') 
       win_logical = True

1. 上一步应该产生以下交互输出：

Input index of your move (0-8): 4
Model has moved
 O |   |
___________ 
   | X | 
___________ 
   |   | 
Input index of your move (0-8): 6 
Model has moved 
O  |   | 
___________ 
   | X | 
___________ 
 X |   | O 
Input index of your move (0-8): 2 
Model has moved 
O  |   | X 
___________ 
O  | X | 
___________ 
X  |   | O 
Game Over!

工作原理

在本节中，我们通过馈送棋盘位置和九维向量训练神经网络来玩井字棋，并预测最佳响应。我们只需要喂几个可能的井字棋棋盘并对每个棋盘应用随机变换以增加训练集大小。

为了测试我们的算法，我们删除了一个特定棋盘的所有实例，并查看我们的模型是否可以推广以预测最佳响应。最后，我们针对我们的模型玩了一个示例游戏。虽然它还不完善，但仍有不同的架构和训练程序可用于改进它。