评估模型

我们已经学会了如何在 TensorFlow 中训练回归和分类算法。在此之后，我们必须能够评估模型的预测，以确定它的效果。

做好准备

评估模型非常重要，每个后续模型都将采用某种形式的模型评估。使用 TensorFlow，我们必须将此函数构建到计算图中，并在我们的模型进行训练时和/或完成训练后调用它。

在训练期间评估模型可以让我们深入了解算法，并可以提供调试，改进或完全更改模型的提示。虽然训练期间的评估并不总是必要的，但我们将展示如何使用回归和分类进行评估。

训练结束后，我们需要量化模型对数据的执行方式。理想情况下，我们有一个单独的训练和测试集（甚至是验证集），我们可以在其上评估模型。

当我们想要评估模型时，我们希望在大批数据点上进行评估。如果我们已经实现了批量训练，我们可以重用我们的模型来对这样的批次进行预测。如果我们实现了随机训练，我们可能必须创建一个可以批量处理数据的单独评估器。

如果我们在loss函数中包含对模型输出的转换，例如sigmoid_cross_entropy_with_logits()，我们必须在计算精度计算的预测时考虑到这一点。不要忘记将此包含在您对模型的评估中。

我们要评估的任何模型的另一个重要方面是它是回归还是分类模型。

回归模型试图预测连续数。目标不是类别，而是所需数量。为了评估这些针对实际目标的回归预测，我们需要对两者之间的距离进行综合测量。大多数情况下，有意义的损失函数将满足这些标准。此秘籍向您展示如何将之前的简单回归算法更改为打印出训练循环中的损失并在结束时评估损失。例如，我们将在本章的先前实现反向传播秘籍中重新审视并重写我们的回归示例。

分类模型基于数字输入预测类别。实际目标是 1 和 0 的序列，我们必须衡量我们与预测的真实程度。分类模型的损失函数通常对解释模型的运行情况没有帮助。通常，我们需要某种分类准确率，这通常是正确预测类别的百分比。对于此示例，我们将使用本章中先前实现反向传播秘籍的分类示例。

操作步骤

首先，我们将展示如何评估简单回归模型，该模型简单地适应目标的常数乘法，即 10，如下所示：

1. 首先，我们首先加载库并创建图，数据，变量和占位符。本节还有一个非常重要的部分。在我们创建数据之后，我们将数据随机分成训练和测试数据集。这很重要，因为我们总是会测试我们的模型，看看它们是否预测良好。在训练数据和测试数据上评估模型还可以让我们看到模型是否过拟合：

import matplotlib.pyplot as plt 
import numpy as np 
import tensorflow as tf 
sess = tf.Session() 
x_vals = np.random.normal(1, 0.1, 100) 
y_vals = np.repeat(10., 100) 
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32) 
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) 
batch_size = 25 
train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False) 
test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices))) 
x_vals_train = x_vals[train_indices] 
x_vals_test = x_vals[test_indices] 
y_vals_train = y_vals[train_indices] 
y_vals_test = y_vals[test_indices] 
A = tf.Variable(tf.random_normal(shape=[1,1]))

1. 现在，我们声明我们的模型，loss函数和优化算法。我们还将初始化模型变量A。使用以下代码：

my_output = tf.matmul(x_data, A) 
loss = tf.reduce_mean(tf.square(my_output - y_target))
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
init = tf.global_variables_initializer() 
sess.run(init)

1. 我们正如我们之前看到的那样运行训练循环，如下所示：

for i in range(100): 
    rand_index = np.random.choice(len(x_vals_train), size=batch_size) rand_x = np.transpose([x_vals_train[rand_index]]) 
    rand_y = np.transpose([y_vals_train[rand_index]]) 
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) 
    if (i + 1) % 25 == 0: 
        print('Step #' + str(i+1) + ' A = ' + str(sess.run(A))) 
        print('Loss = ' + str(sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}))) 
Step #25 A = [[ 6.39879179]] 
Loss = 13.7903 
Step #50 A = [[ 8.64770794]] 
Loss = 2.53685 
Step #75 A = [[ 9.40029907]] 
Loss = 0.818259 
Step #100 A = [[ 9.6809473]] 
Loss = 1.10908

1. 现在，为了评估模型，我们将在训练和测试集上输出 MSE（损失函数），如下所示：

mse_test = sess.run(loss, feed_dict={x_data: np.transpose([x_vals_test]), y_target: np.transpose([y_vals_test])}) 
mse_train = sess.run(loss, feed_dict={x_data: np.transpose([x_vals_train]), y_target: np.transpose([y_vals_train])}) 
print('MSE' on test:' + str(np.round(mse_test, 2))) 
print('MSE' on train:' + str(np.round(mse_train, 2))) 
MSE on test:1.35 
MSE on train:0.88

对于分类示例，我们将做一些非常相似的事情。这一次，我们需要创建我们自己的精确度函数，我们可以在最后调用。其中一个原因是我们的损失函数内置了 sigmoid，我们需要单独调用 sigmoid 并测试它以查看我们的类是否正确：

1. 在同一个脚本中，我们可以重新加载图并创建数据，变量和占位符。请记住，我们还需要将数据和目标分成训练和测试集。使用以下代码：

from tensorflow.python.framework import ops 
ops.reset_default_graph() 
sess = tf.Session() 
batch_size = 25 
x_vals = np.concatenate((np.random.normal(-1, 1, 50), np.random.normal(2, 1, 50))) 
y_vals = np.concatenate((np.repeat(0., 50), np.repeat(1., 50))) 
x_data = tf.placeholder(shape=[1, None], dtype=tf.float32) 
y_target = tf.placeholder(shape=[1, None], dtype=tf.float32) 
train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False) 
test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices))) 
x_vals_train = x_vals[train_indices] 
x_vals_test = x_vals[test_indices] 
y_vals_train = y_vals[train_indices] 
y_vals_test = y_vals[test_indices] 
A = tf.Variable(tf.random_normal(mean=10, shape=[1]))

1. 我们现在将模型和损失函数添加到图中，初始化变量，并创建优化过程，如下所示：

my_output = tf.add(x_data, A) 
init = tf.initialize_all_variables() 
sess.run(init) 
xentropy = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(my_output, y_target)) 
my_opt = tf.train.GradientDescentOptimizer(0.05) 
train_step = my_opt.minimize(xentropy)

1. 现在，我们运行我们的训练循环，如下所示：

for i in range(1800): 
    rand_index = np.random.choice(len(x_vals_train), size=batch_size) 
    rand_x = [x_vals_train[rand_index]] 
    rand_y = [y_vals_train[rand_index]] 
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) 
    if (i+1)%200==0: 
        print('Step #' + str(i+1) + ' A = ' + str(sess.run(A))) 
        print('Loss = ' + str(sess.run(xentropy, feed_dict={x_data: rand_x, y_target: rand_y}))) 
Step #200 A = [ 6.64970636] 
Loss = 3.39434 
Step #400 A = [ 2.2884655] 
Loss = 0.456173 
Step #600 A = [ 0.29109824] 
Loss = 0.312162 
Step #800 A = [-0.20045301] 
Loss = 0.241349 
Step #1000 A = [-0.33634067] 
Loss = 0.376786 
Step #1200 A = [-0.36866501] 
Loss = 0.271654 
Step #1400 A = [-0.3727718] 
Loss = 0.294866 
Step #1600 A = [-0.39153299] 
Loss = 0.202275 
Step #1800 A = [-0.36630616] 
Loss = 0.358463

1. 为了评估模型，我们将创建自己的预测操作。我们将预测操作包装在挤压函数中，因为我们希望使预测和目标形成相同的形状。然后，我们用相等的函数测试相等性。在那之后，我们留下了一个真值和假值的张量，我们将其转换为float32并取平均值。这将产生准确率值。我们将为训练集和测试集评估此函数，如下所示：

y_prediction = tf.squeeze(tf.round(tf.nn.sigmoid(tf.add(x_data, A)))) 
correct_prediction = tf.equal(y_prediction, y_target) 
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) 
acc_value_test = sess.run(accuracy, feed_dict={x_data: [x_vals_test], y_target: [y_vals_test]}) 
acc_value_train = sess.run(accuracy, feed_dict={x_data: [x_vals_train], y_target: [y_vals_train]}) 
print('Accuracy' on train set: ' + str(acc_value_train)) 
print('Accuracy' on test set: ' + str(acc_value_test)) 
Accuracy on train set: 0.925 
Accuracy on test set: 0.95

1. 通常，查看模型结果（准确率，MSE 等）将有助于我们评估模型。我们可以在这里轻松绘制模型和数据的绘图，因为它是一维的。以下是使用matplotlib使用两个单独的直方图可视化模型和数据的方法：

A_result = sess.run(A) 
bins = np.linspace(-5, 5, 50) 
plt.hist(x_vals[0:50], bins, alpha=0.5, label='N(-1,1)', color='white') 
plt.hist(x_vals[50:100], bins[0:50], alpha=0.5, label='N(2,1)', color='red') 
plt.plot((A_result, A_result), (0, 8), 'k--', linewidth=3, label='A = '+ str(np.round(A_result, 2))) 
plt.legend(loc='upper right') 
plt.title('Binary Classifier, Accuracy=' + str(np.round(acc_value, 2))) 
plt.show()

工作原理

这导致绘图显示两个单独数据类的直方图中两个类的预测最佳分隔符。

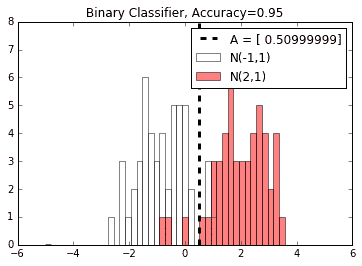
图 8：数据和结束模型的可视化，A。两个正常值以-1 和 2 为中心，使理论最佳分割为 0.5。在这里，模型发现最接近该数字的最佳分割。