使用 k 均值聚类

TensorFlow 还可用于实现迭代聚类算法，例如 k-means。在本文中，我们展示了在iris数据集上使用 k-means 的示例。

做好准备

我们在本书中探讨的几乎所有机器学习模型都是监督模型。 TensorFlow 非常适合这些类型的问题。但是，如果我们愿意，我们也可以实现无人监督的模型。例如，此秘籍将实现 k-means 聚类。

我们将实现聚类的数据集是iris数据集。这是一个很好的数据集的原因之一是因为我们已经知道有三种不同的目标（三种类型的鸢尾花）。这让我们知道我们正在寻找数据中的三个不同的集群。

我们将iris数据集聚类为三组，然后将这些聚类的准确率与实际标签进行比较。

操作步骤

1. 首先，我们加载必要的库。我们还从sklearn加载了一些 PCA 工具，以便我们可以将结果数据从四维更改为二维，以实现可视化目的：

import numpy as np 
import matplotlib.pyplot as plt 
import tensorflow as tf 
from sklearn import datasets 
from scipy.spatial import cKDTree 
from sklearn.decomposition import PCA 
from sklearn.preprocessing import scale

1. 我们启动图会话，并加载iris数据集：

sess = tf.Session() 
iris = datasets.load_iris() 
num_pts = len(iris.data) 
num_feats = len(iris.data[0])

1. 我们现在将设置组，代，并创建图所需的变量：

k=3  
generations = 25 
data_points = tf.Variable(iris.data) 
cluster_labels = tf.Variable(tf.zeros([num_pts], dtype=tf.int64))

1. 我们需要的下一个变量是每组的质心。我们将通过随机选择iris数据集的三个不同点来初始化 k-means 算法的质心：

rand_starts = np.array([iris.data[np.random.choice(len(iris.data))] for _ in range(k)]) 
centroids = tf.Variable(rand_starts)

1. 现在，我们需要计算每个数据点和每个centroids之间的距离。我们通过将centroids扩展为矩阵来实现这一点，对数据点也是如此。然后我们将计算两个矩阵之间的欧几里德距离：

centroid_matrix = tf.reshape(tf.tile(centroids, [num_pts, 1]), [num_pts, k, num_feats]) 
point_matrix = tf.reshape(tf.tile(data_points, [1, k]), [num_pts, k, num_feats]) 
distances = tf.reduce_sum(tf.square(point_matrix - centroid_matrix), reduction_indices=2)

1. centroids赋值是每个数据点最接近的centroids（最小距离）：

centroid_group = tf.argmin(distances, 1)

1. 现在，我们必须计算组平均值以获得新的质心：

def data_group_avg(group_ids, data): 
    # Sum each group 
    sum_total = tf.unsorted_segment_sum(data, group_ids, 3) 
    # Count each group 
    num_total = tf.unsorted_segment_sum(tf.ones_like(data), group_ids, 3) 
    # Calculate average 
    avg_by_group = sum_total/num_total 
    return(avg_by_group) 
means = data_group_avg(centroid_group, data_points) 
update = tf.group(centroids.assign(means), cluster_labels.assign(centroid_group))

1. 接下来，我们初始化模型变量：

init = tf.global_variables_initializer() 
sess.run(init)

1. 我们将遍历几代并相应地更新每个组的质心：

for i in range(generations): 
    print('Calculating gen {}, out of {}.'.format(i, generations)) 
    _, centroid_group_count = sess.run([update, centroid_group]) 
    group_count = [] 
    for ix in range(k): 
        group_count.append(np.sum(centroid_group_count==ix)) 
    print('Group counts: {}'.format(group_count))

1. 这导致以下输出：

Calculating gen 0, out of 25\. Group counts: [50, 28, 72] Calculating gen 1, out of 25\. Group counts: [50, 35, 65] Calculating gen 23, out of 25\. Group counts: [50, 38, 62] Calculating gen 24, out of 25\. Group counts: [50, 38, 62]

1. 为了验证我们的聚类，我们可以使用聚类进行预测。我们现在看到有多少数据点位于相同虹膜种类的相似簇中：

[centers, assignments] = sess.run([centroids, cluster_labels]) 
def most_common(my_list): 
    return(max(set(my_list), key=my_list.count)) 
label0 = most_common(list(assignments[0:50])) 
label1 = most_common(list(assignments[50:100])) 
label2 = most_common(list(assignments[100:150])) 
group0_count = np.sum(assignments[0:50]==label0) 
group1_count = np.sum(assignments[50:100]==label1) 
group2_count = np.sum(assignments[100:150]==label2) 
accuracy = (group0_count + group1_count + group2_count)/150\. 
print('Accuracy: {:.2}'.format(accuracy))

1. 这导致以下输出：

Accuracy: 0.89

1. 为了直观地看到我们的分组，如果它们确实已经分离出iris物种，我们将使用 PCA 将四维转换为二维，并绘制数据点和组。在 PCA 分解之后，我们在 x-y 值网格上创建预测，以绘制颜色图：

pca_model = PCA(n_components=2) 
reduced_data = pca_model.fit_transform(iris.data) 
# Transform centers 
reduced_centers = pca_model.transform(centers) 
# Step size of mesh for plotting 
h = .02 
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1 
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1 
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))  
# Get k-means classifications for the grid points 
xx_pt = list(xx.ravel()) 
yy_pt = list(yy.ravel()) 
xy_pts = np.array([[x,y] for x,y in zip(xx_pt, yy_pt)]) 
mytree = cKDTree(reduced_centers) 
dist, indexes = mytree.query(xy_pts) 
indexes = indexes.reshape(xx.shape)

1. 并且，这里是matplotlib代码将我们的发现结合在一个绘图上。这个密码的绘图部分很大程度上改编自 scikit-learn（ http://scikit-learn.org/ ）文档网站上的演示（ http://scikit-learn.org/ stable / auto_examples / cluster / plot_kmeans_digits.html ）：

plt.clf() 
plt.imshow(indexes, interpolation='nearest', 
           extent=(xx.min(), xx.max(), yy.min(), yy.max()), 
           cmap=plt.cm.Paired, 
           aspect='auto', origin='lower') 
# Plot each of the true iris data groups 
symbols = ['o', '^', 'D'] 
label_name = ['Setosa', 'Versicolour', 'Virginica'] 
for i in range(3): 
    temp_group = reduced_data[(i*50):(50)*(i+1)] 
    plt.plot(temp_group[:, 0], temp_group[:, 1], symbols[i], markersize=10, label=label_name[i]) 
# Plot the centroids as a white X 
plt.scatter(reduced_centers[:, 0], reduced_centers[:, 1], 
            marker='x', s=169, linewidths=3, 
            color='w', zorder=10) 
plt.title('K-means clustering on Iris Datasets' 
          'Centroids are marked with white cross') 
plt.xlim(x_min, x_max) 
plt.ylim(y_min, y_max) 
plt.legend(loc='lower right') 
plt.show()

这个绘图代码将向我们展示三个类，三个类的预测空间以及每个组的质心：

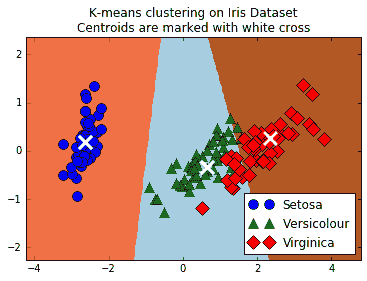
图 5：显示 k-means 的无监督分类算法的屏幕截图;可以用来将三种鸢尾花种组合在一起。三个 k-means 组是三个阴影区域，三个不同的点（圆，三角形和菱形）是三个真正的物种分类

更多

对于此秘籍，我们使用 TensorFlow 将iris数据集聚类为三组。然后，我们计算了落入相似组的数据点的百分比（89％），并绘制了所得 k-均值组的图。由于 k-means 作为分类算法是局部线性的（线性分离器向上），因此很难学习虹膜鸢尾和 Iris virginica 之间的天然非线性边界。但是，一个优点是 k-means 算法根本不需要标记数据来执行。