实现逻辑回归

对于这个秘籍，我们将实现逻辑回归来预测样本人群中低出生体重的概率。

做好准备

逻辑回归是将线性回归转换为二元分类的一种方法。这是通过将线性输出转换为 Sigmoid 函数来实现的，该函数将输出在 0 和 1 之间进行缩放。目标是零或一，表示数据点是在一个类还是另一个类中。由于我们预测 0 和 1 之间的数字，如果预测高于指定的截止值，则预测被分类为类值 1，否则分类为 0。出于此示例的目的，我们将指定 cutoff 为 0.5，这将使分类像舍入输出一样简单。

我们将用于此示例的数据将是从作者的 GitHub 仓库获得的低出生体重数据（ https://github.com/nfmcclure/tensorflow_cookbook/raw/master/01_Introduction/07_Working_with_Data_Sources/birthweight_data/birthweight.dat ）。我们将从其他几个因素预测低出生体重。

操作步骤

我们按如下方式处理秘籍：

1. 我们首先加载库，包括request库，因为我们将通过超链接访问低出生体重数据。我们还发起了一个会议：

import matplotlib.pyplot as plt 
import numpy as np 
import tensorflow as tf 
import requests 
from sklearn import datasets 
from sklearn.preprocessing import normalize 
from tensorflow.python.framework import ops 
ops.reset_default_graph() 
sess = tf.Session()

1. 接下来，我们通过请求模块加载数据并指定我们要使用的特征。我们必须具体，因为一个特征是实际出生体重，我们不想用它来预测出生体重是大于还是小于特定量。我们也不想将 ID 列用作预测器：

birth_weight_file = 'birth_weight.csv'
# Download data and create data file if file does not exist in current directory
if not os.path.exists(birth_weight_file):
    birthdata_url = 'https://github.com/nfmcclure/tensorflow_cookbook/raw/master/01_Introduction/07_Working_with_Data_Sources/birthweight_data/birthweight.dat'
    birth_file = requests.get(birthdata_url)
    birth_data = birth_file.text.split('\r\n')
    birth_header = birth_data[0].split('\t')
    birth_data = [[float(x) for x in y.split('\t') if len(x)>=1] for y in birth_data[1:] if len(y)>=1]
    with open(birth_weight_file, 'w', newline='') as f:
        writer = csv.writer(f)
        writer.writerow(birth_header)
        writer.writerows(birth_data)

# Read birth weight data into memory
birth_data = []
with open(birth_weight_file, newline='') as csvfile:
    csv_reader = csv.reader(csvfile)
    birth_header = next(csv_reader)
    for row in csv_reader:
        birth_data.append(row)
    birth_data = [[float(x) for x in row] for row in birth_data]
# Pull out target variable
y_vals = np.array([x[0] for x in birth_data])
# Pull out predictor variables (not id, not target, and not birthweight)
x_vals = np.array([x[1:8] for x in birth_data])

1. 首先，我们将数据集拆分为测试和训练集：

train_indices = np.random.choice(len(x_vals), round(len(x_vals)*0.8), replace=False) 
test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices))) 
x_vals_train = x_vals[train_indices] 
x_vals_test = x_vals[test_indices] 
y_vals_train = y_vals[train_indices] 
y_vals_test = y_vals[test_indices]

1. 当特征在 0 和 1 之间缩放（最小 - 最大缩放）时，逻辑回归收敛效果更好。那么，接下来我们将扩展每个特征：

def normalize_cols(m, col_min=np.array([None]), col_max=np.array([None])):
    if not col_min[0]:
        col_min = m.min(axis=0)
    if not col_max[0]:
        col_max = m.max(axis=0)
    return (m-col_min) / (col_max - col_min), col_min, col_max

x_vals_train, train_min, train_max = np.nan_to_num(normalize_cols(x_vals_train))
x_vals_test = np.nan_to_num(normalize_cols(x_vals_test, train_min, train_max))

请注意，在缩放数据集之前，我们将数据集拆分为 train 和 test。这是一个重要的区别。我们希望确保测试集完全不影响训练集。如果我们在分裂之前缩放整个集合，那么我们不能保证它们不会相互影响。我们确保从训练组中保存缩放以缩放测试集。

1. 接下来，我们声明批量大小，占位符，变量和逻辑模型。我们不将输出包装在 sigmoid 中，因为该操作内置于 loss 函数中。另请注意，每次观察都有七个输入特征，因此x_data占位符的大小为[None, 7]。

batch_size = 25 
x_data = tf.placeholder(shape=[None, 7], dtype=tf.float32) 
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) 
A = tf.Variable(tf.random_normal(shape=[7,1])) 
b = tf.Variable(tf.random_normal(shape=[1,1])) 
model_output = tf.add(tf.matmul(x_data, A), b)

1. 现在，我们声明我们的损失函数，它具有 sigmoid 函数，初始化我们的变量，并声明我们的优化函数：

loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(model_output, y_target)) 
init = tf.global_variables_initializer() 
sess.run(init) 
my_opt = tf.train.GradientDescentOptimizer(0.01) 
train_step = my_opt.minimize(loss)

1. 在记录损失函数的同时，我们还希望在训练和测试集上记录分类准确率。因此，我们将创建一个预测函数，返回任何大小的批量的准确率：

prediction = tf.round(tf.sigmoid(model_output)) 
predictions_correct = tf.cast(tf.equal(prediction, y_target), tf.float32) 
accuracy = tf.reduce_mean(predictions_correct)

1. 现在，我们可以开始我们的训练循环并记录损失和准确率：

loss_vec = [] 
train_acc = [] 
test_acc = [] 
for i in range(1500): 
    rand_index = np.random.choice(len(x_vals_train), size=batch_size) 
    rand_x = x_vals_train[rand_index] 
    rand_y = np.transpose([y_vals_train[rand_index]]) 
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) 
    temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) 
    loss_vec.append(temp_loss) 
    temp_acc_train = sess.run(accuracy, feed_dict={x_data: x_vals_train, y_target: np.transpose([y_vals_train])}) 
    train_acc.append(temp_acc_train) 
    temp_acc_test = sess.run(accuracy, feed_dict={x_data: x_vals_test, y_target: np.transpose([y_vals_test])}) 
    test_acc.append(temp_acc_test)

1. 以下是查看损失和准确率图的代码：

plt.plot(loss_vec, 'k-') 
plt.title('Cross' Entropy Loss per Generation') 
plt.xlabel('Generation') 
plt.ylabel('Cross' Entropy Loss') 
plt.show() 
plt.plot(train_acc, 'k-', label='Train Set Accuracy') 
plt.plot(test_acc, 'r--', label='Test Set Accuracy') 
plt.title('Train and Test Accuracy') 
plt.xlabel('Generation') 
plt.ylabel('Accuracy') 
plt.legend(loc='lower right') 
plt.show()

工作原理

这是迭代和训练和测试精度的损失。由于数据集仅为 189 次观测，因此随着数据集的随机分裂，训练和测试精度图将发生变化。第一个数字是交叉熵损失：

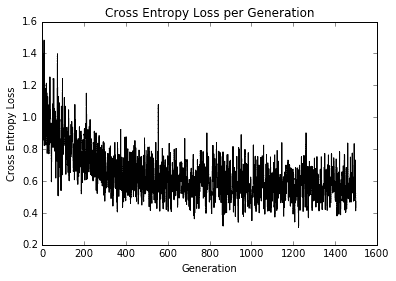
图 11：在 1,500 次迭代过程中绘制的交叉熵损失

第二个图显示了训练和测试装置的准确率：

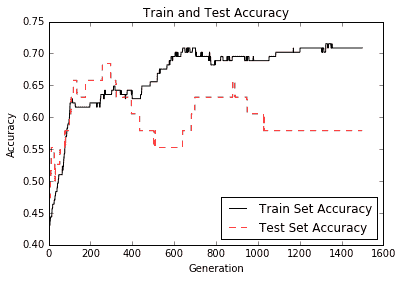Figure 12: Test and train set accuracy plotted over 1,500 generations