介绍

在数学中，卷积是应用于另一个函数的输出的函数。在我们的例子中，我们将考虑在图像上应用矩阵乘法（滤波器）。出于我们的目的，我们将图像视为数字矩阵。这些数字可以表示像素或甚至图像属性。我们将应用于这些矩阵的卷积运算包括在图像上移动固定宽度的滤波器并应用逐元素乘法来得到我们的结果。

有关图像卷积如何工作的概念性理解，请参见下图：

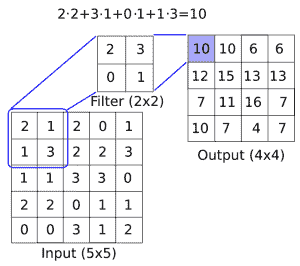
图 1：如何在图像上应用卷积滤镜（长度与宽度之间的深度），以创建新的特征层。这里，我们有一个2x2卷积滤波器，在5x5输入的有效空间中操作，两个方向的步幅为 1。结果是4x4矩阵

CNN 还具有满足更多要求的其他操作，例如引入非线性（ReLU）或聚合参数（max P \ pool）以及其他类似操作。上图是在5x5数组上应用卷积运算的示例，其中卷积滤波器是2x2矩阵。步长为 1，我们只考虑有效的展示位置。此操作中的可训练变量将是2x2滤波器权重。在卷积之后，通常会跟进聚合操作，例如 max pool。如果我们在两个方向上采用步幅为 2 的2x2区域的最大值，下图提供了最大池如何操作的示例：

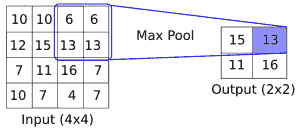
图 2：Max Pool 操作如何运行的示例。这里，我们有一个2x2窗口，在4x4输入的有效空间上操作，两个方向的步幅为 2。结果是2x2矩阵

虽然我们将首先创建自己的 CNN 进行图像识别，但强烈建议您使用现有的体系结构，我们将在本章的其余部分中进行操作。

通常采用预先训练好的网络并使用新数据集对其进行重新训练，并在最后使用新的完全连接层。这种方法非常有用，我们将在重新训练现有的 CNN 模型秘籍中进行说明，我们将重新训练现有的体系结构以改进我们的 CIFAR-10 预测。