把所有东西结合在一起
在本节中,我们将结合到目前为止所示的所有内容,并为虹膜数据集创建分类器。
做好准备
虹膜数据集在第 1 章,TensorFlow 入门中使用数据源秘籍中有更详细的描述。我们将加载这些数据并制作一个简单的二元分类器来预测花是否是 Iris setosa 的种类。需要说明的是,这个数据集有三个种类,但我们只能预测一种花是单一种,是否是一种花,给我们一个二元分类器。我们将首先加载库和数据,然后相应地转换目标。
操作步骤
我们按如下方式处理秘籍:
- 首先,我们加载所需的库并初始化计算图。注意我们也在这里加载
matplotlib,因为我们想在之后绘制结果行:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
import tensorflow as tf
sess = tf.Session()
- 接下来,我们加载虹膜数据。我们还需要将目标数据转换为 1 或 0,无论目标是否为 setosa。由于虹膜数据集将 setosa 标记为 0,我们将更改所有目标,值为 0 到 1,其他值全部为 0.我们也将只使用两个特征,花瓣长度和花瓣宽度。这两个特征是每个
x-value中的第三和第四个条目:
iris = datasets.load_iris()
binary_target = np.array([1\. if x==0 else 0\. for x in iris.target])
iris_2d = np.array([[x[2], x[3]] for x in iris.data])
- 让我们声明我们的批量大小,数据占位符和模型变量。请记住,可变批量大小的数据占位符将
None作为第一个维度:
batch_size = 20
x1_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
x2_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
A = tf.Variable(tf.random_normal(shape=[1, 1]))
b = tf.Variable(tf.random_normal(shape=[1, 1]))
请注意,我们可以通过使用
dtype=tf.float32来减少浮点数的字节来提高算法的表现(速度)。
- 在这里,我们定义线性模型。模型将采用
x2 = x1 * A + b的形式,如果我们想要找到该行上方或下方的点,我们会在插入等式x2 - x1 * A - b时看到它们是高于还是低于零。我们将通过取该方程的 sigmoid 并从该方程预测 1 或 0 来实现。请记住,TensorFlow 具有内置 sigmoid 的loss函数,因此我们只需要在 sigmoid 函数之前定义模型的输出:
my_mult = tf.matmul(x2_data, A)
my_add = tf.add(my_mult, b)
my_output = tf.sub(x1_data, my_add)
- 现在,我们使用 TensorFlow 的内置
sigmoid_cross_entropy_with_logits()函数添加 sigmoid 交叉熵损失函数:
xentropy = tf.nn.sigmoid_cross_entropy_with_logits(my_output, y_target)
- 我们还必须告诉 TensorFlow 如何通过声明优化方法来优化我们的计算图。我们希望最大限度地减少交叉熵损失。我们还会选择
0.05作为我们的学习率:
my_opt = tf.train.GradientDescentOptimizer(0.05)
train_step = my_opt.minimize(xentropy)
- 现在,我们创建一个变量初始化操作并告诉 TensorFlow 执行它:
init = tf.global_variables_initializer()
sess.run(init)
- 现在,我们将训练我们的线性模型 1000 次迭代。我们将提供我们需要的三个数据点:花瓣长度,花瓣宽度和目标变量。每 200 次迭代,我们将打印变量值:
for i in range(1000):
rand_index = np.random.choice(len(iris_2d), size=batch_size)
rand_x = iris_2d[rand_index]
rand_x1 = np.array([[x[0]] for x in rand_x])
rand_x2 = np.array([[x[1]] for x in rand_x])
rand_y = np.array([[y] for y in binary_target[rand_index]])
sess.run(train_step, feed_dict={x1_data: rand_x1, x2_data: rand_x2, y_target: rand_y})
if (i + 1) % 200 == 0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ', b = ' + str(sess.run(b)))
Step #200 A = [[ 8.67285347]], b = [[-3.47147632]]
Step #400 A = [[ 10.25393486]], b = [[-4.62928772]]
Step #600 A = [[ 11.152668]], b = [[-5.4077611]]
Step #800 A = [[ 11.81016064]], b = [[-5.96689034]]
Step #1000 A = [[ 12.41202831]], b = [[-6.34769201]]
- 下一组命令提取模型变量并在绘图上绘制线条。结果绘图在它的工作原理...部分:
[[slope]] = sess.run(A)
[[intercept]] = sess.run(b)
x = np.linspace(0, 3, num=50)
ablineValues = []
for i in x:
ablineValues.append(slope*i+intercept)
setosa_x = [a[1] for i,a in enumerate(iris_2d) if binary_target[i]==1]
setosa_y = [a[0] for i,a in enumerate(iris_2d) if binary_target[i]==1]
non_setosa_x = [a[1] for i,a in enumerate(iris_2d) if binary_target[i]==0]
non_setosa_y = [a[0] for i,a in enumerate(iris_2d) if binary_target[i]==0]
plt.plot(setosa_x, setosa_y, 'rx', ms=10, mew=2, label='setosa')
plt.plot(non_setosa_x, non_setosa_y, 'ro', label='Non-setosa')
plt.plot(x, ablineValues, 'b-')
plt.xlim([0.0, 2.7])
plt.ylim([0.0, 7.1])
plt.suptitle('Linear' Separator For I.setosa', fontsize=20)
plt.xlabel('Petal Length')
plt.ylabel('Petal Width')
plt.legend(loc='lower right')
plt.show()
工作原理
我们的目标是仅使用花瓣宽度和花瓣长度在 I. setosa 点和其他两个物种之间拟合一条线。如果我们绘制点和结果线,我们看到我们已经实现了这个:
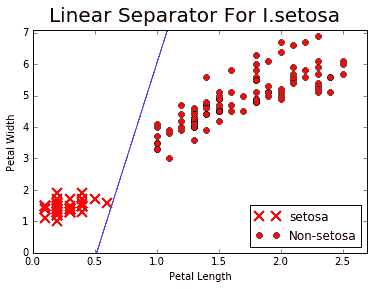
图 7:花瓣宽度与花瓣长度的 I. setosa 和 non-setosa 的图;实线是我们在 1000 次迭代后实现的线性分离器
更多
虽然我们实现了用一条线分隔两个类的目标,但它可能不是分离两个类的最佳模型。在第 4 章,支持向量机中,我们将讨论支持向量机,它是在特征空间中分离两个类的更好方法。
另见
- 有关 scikit-learn iris 数据集实现的信息,请参阅 http://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html 上的文档。