使用批量和随机训练
虽然 TensorFlow 根据反向传播更新我们的模型变量,但它可以同时操作从一个基准观察到一大批数据的任何事物。在一个训练示例上操作可以使得学习过程非常不稳定,而使用太大的批次可能在计算上是昂贵的。选择正确类型的训练对于使我们的机器学习算法融合到解决方案至关重要。
做好准备
为了使 TensorFlow 计算反向传播的可变梯度,我们必须测量样本或多个样本的损失。随机训练一次只适用于一个随机抽样的数据 - 目标对,就像我们在上一个秘籍中所做的那样。另一种选择是一次放置大部分训练样例并平均梯度计算的损失。训练批次的大小可以一次变化,直到并包括整个数据集。在这里,我们将展示如何将先前的回归示例(使用随机训练)扩展到批量训练。
我们将首先加载numpy,matplotlib和tensorflow,然后开始图会话,如下所示:
import matplotlib as plt
import numpy as np
import tensorflow as tf
sess = tf.Session()
操作步骤
我们按如下方式处理秘籍:
- 我们将从声明批量大小开始。这将是我们将同时通过计算图提供多少数据观察:
batch_size = 20
- 接下来,我们在模型中声明数据,占位符和变量。我们在这里做的改变是我们改变了占位符的形状。它们现在是两个维度,第一个维度是
None,第二个维度是批次中的数据点数。我们可以明确地将它设置为 20,但我们可以推广并使用None值。同样,正如第 1 章,TensorFlow 入门中所述,我们仍然需要确保维度在模型中运行,这不允许我们执行任何非法矩阵操作:
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
A = tf.Variable(tf.random_normal(shape=[1,1]))
- 现在,我们将操作添加到图中,现在将是矩阵乘法而不是常规乘法。请记住,矩阵乘法不是可交换的,因此我们必须在
matmul()函数中以正确的顺序输入矩阵:
my_output = tf.matmul(x_data, A)
- 我们的
loss函数会发生变化,因为我们必须采用批次中每个数据点的所有 L2 损失的平均值。我们通过将先前的损失输出包装在 TensorFlow 的reduce_mean()函数中来实现:
loss = tf.reduce_mean(tf.square(my_output - y_target))
- 我们像以前一样声明我们的优化器并初始化我们的模型变量,如下所示:
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
init = tf.global_variables_initializer()
sess.run(init)
- 最后,我们将循环并迭代训练步骤以优化算法。这部分与以前不同,因为我们希望能够绘制随时间的损失并比较批次与随机训练的收敛。因此,我们初始化一个列表,每隔五个时间间隔存储一次损失函数:
loss_batch = []
for i in range(100):
rand_index = np.random.choice(100, size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i + 1) % 5 == 0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_batch.append(temp_loss)
- 这是 100 次迭代的最终输出。请注意,
A的值有一个额外的维度,因为它现在必须是一个 2D 矩阵:
Step #100 A = [[ 9.86720943]]
Loss = 0\.
工作原理
批量训练和随机训练的优化方法和收敛性不同。找到一个好的批量大小可能很困难。为了了解批量与随机指标之间的收敛程度如何不同,建议读者将批量大小更改为各种级别。以下是保存和记录训练循环中随机损失的代码。只需在上一个秘籍中替换此代码:
loss_stochastic = []
for i in range(100):
rand_index = np.random.choice(100)
rand_x = [x_vals[rand_index]]
rand_y = [y_vals[rand_index]]
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i + 1) % 5 == 0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_stochastic.append(temp_loss)
下面是为同一回归问题生成随机和批量损失图的代码:
plt.plot(range(0, 100, 5), loss_stochastic, 'b-', label='Stochastic Loss')
plt.plot(range(0, 100, 5), loss_batch, 'r--', label='Batch' Loss, size=20')
plt.legend(loc='upper right', prop={'size': 11})
plt.show()
我们得到以下绘图:
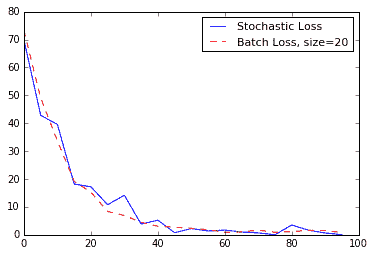
图 6:在 100 次迭代中绘制的随机损失和批量损失(批量大小= 20)。请注意,批次损失更加平滑,随机损失更加不稳定。
更多
| 训练类型 | 好处 | 缺点 |
|---|---|---|
| 随机 | 随机性可能有助于摆脱当地的最低限度。 | 通常,需要更多迭代才能收敛。 |
| 批量 | 更快地找到最小值。 | 需要更多资源来计算。 |