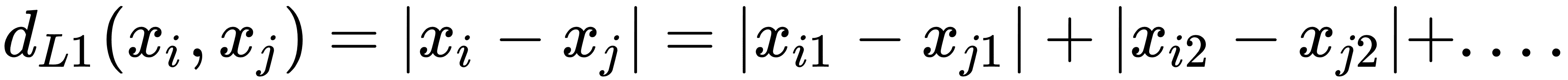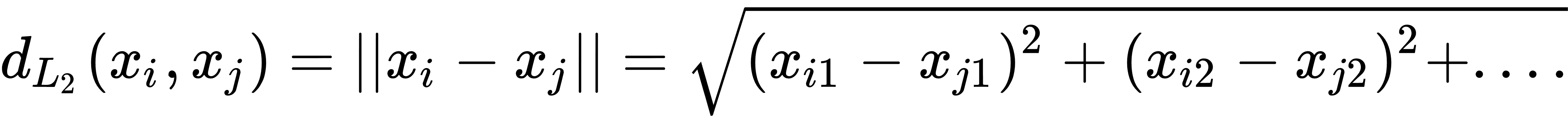介绍

最近邻方法植根于基于距离的概念思想。我们认为我们的训练设定了一个模型，并根据它们与训练集中的点的接近程度对新点进行预测。一种简单的方法是使预测类与最接近的训练数据点类相同。但由于大多数数据集包含一定程度的噪声，因此更常见的方法是采用一组k-最近邻居的加权平均值。该方法称为 k-最近邻居（k-NN）。

给定具有相应目标（y[1], y[2]....y[n]）的训练数据集（x[1],x[2].....x[n]），我们可以通过查看一组最近邻居来对点z进行预测。实际的预测方法取决于我们是进行回归（连续y[i]）还是分类（离散y[i]）。

对于离散分类目标，可以通过最大投票方案给出预测，通过到预测点的距离加权：

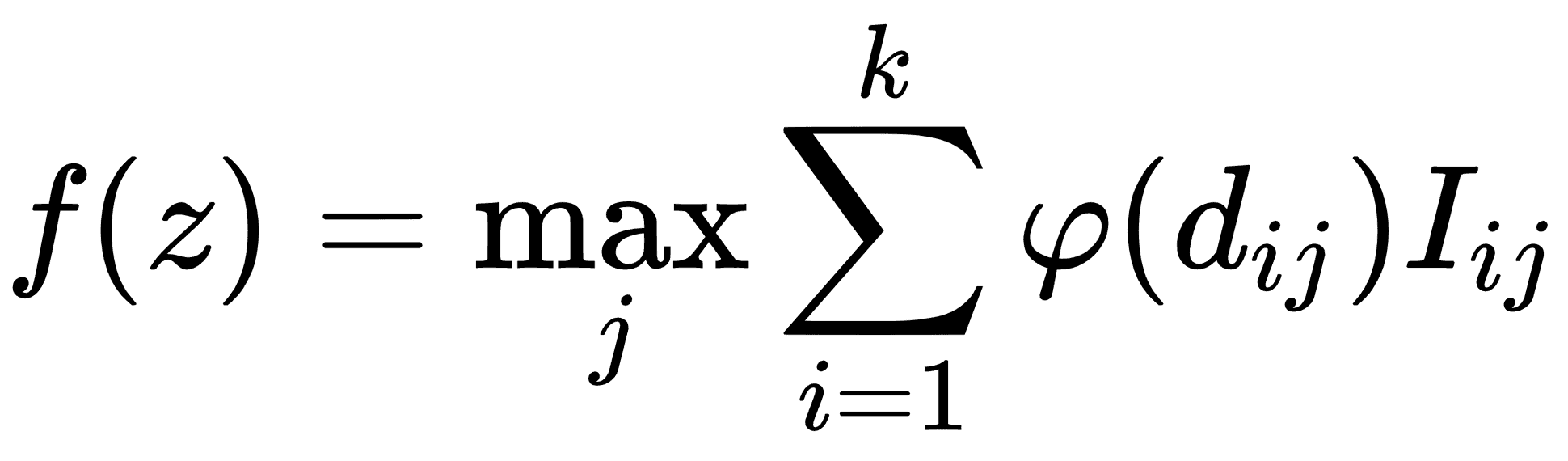
我们这里的预测f(z)是所有类别j的最大加权值，其中从预测点到训练点的加权距离i由φ(d[ij])给出。如果点i在类j.中，l[ij]只是一个指示器函数如果点i在类j中，则指示器函数取值 1，如果不是，则取值 0 另外，k是要考虑的最近点数。

对于连续回归目标，预测由最接近预测的所有k点的加权平均值给出：

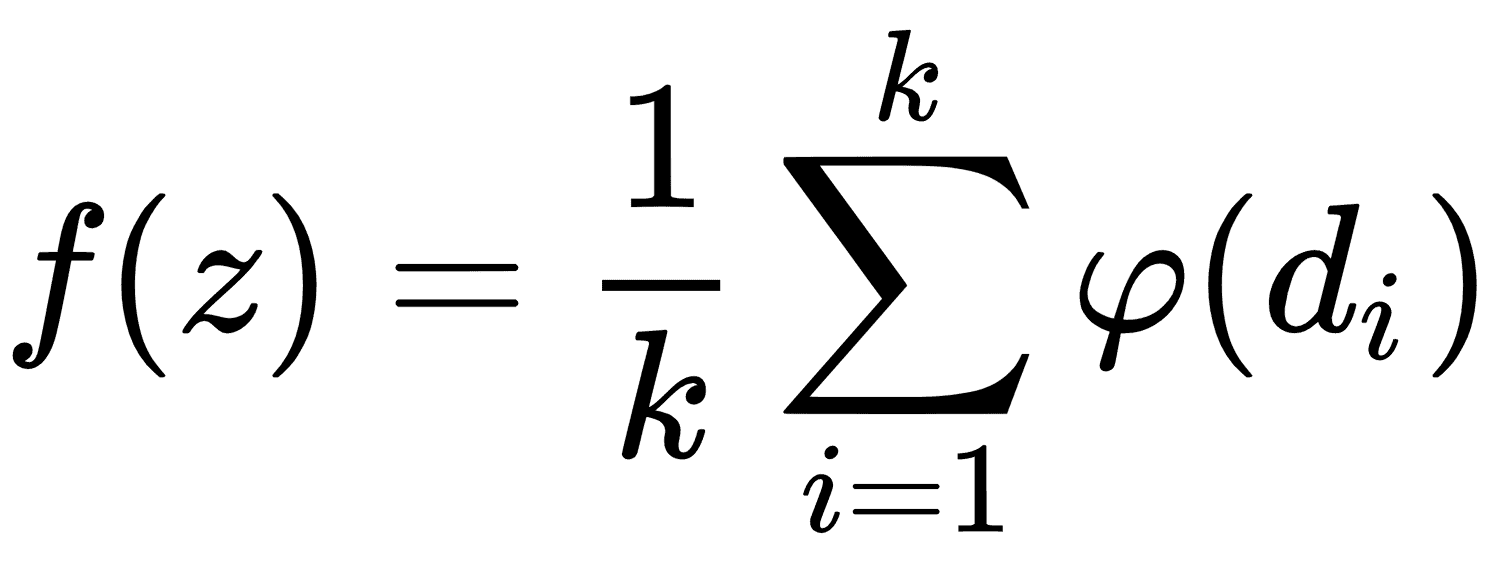
很明显，预测很大程度上取决于距离度量的选择d。

距离度量的常用规范是 L1 和 L2 距离，如下所示：

我们可以选择许多不同规格的距离指标。在本章中，我们将探讨 L1 和 L2 指标，以及编辑和文本距离。

我们还必须选择如何加权距离。对距离进行加权的直接方法是距离本身。远离我们预测的点应该比较近点的影响小。最常见的权重方法是通过距离的归一化逆。我们将在下一个秘籍中实现此方法。

注意，k-NN 是一种聚合方法。对于回归，我们正在执行邻居的加权平均。因此，预测将不那么极端，并且与实际目标相比变化较小。这种影响的大小将由算法中邻居的数量k决定。