实现弹性网络回归

弹性网络回归是一种回归类型，通过将 L1 和 L2 正则化项添加到损失函数，将套索回归与岭回归相结合。

做好准备

在前两个秘籍之后实现弹性网络回归应该是直截了当的，因此我们将在虹膜数据集上的多元线性回归中实现这一点，而不是像以前那样坚持二维数据。我们将使用花瓣长度，花瓣宽度和萼片宽度来预测萼片长度。

操作步骤

我们按如下方式处理秘籍：

1. 首先，我们加载必要的库并初始化图，如下所示：

import matplotlib.pyplot as plt 
import numpy as np 
import tensorflow as tf 
from sklearn import datasets 
sess = tf.Session()

1. 现在，我们加载数据。这次，x数据的每个元素将是三个值的列表而不是一个。使用以下代码：

iris = datasets.load_iris() 
x_vals = np.array([[x[1], x[2], x[3]] for x in iris.data]) 
y_vals = np.array([y[0] for y in iris.data])

1. 接下来，我们声明批量大小，占位符，变量和模型输出。这里唯一的区别是我们更改x数据占位符的大小规范，取三个值而不是一个，如下所示：

batch_size = 50 
learning_rate = 0.001 
x_data = tf.placeholder(shape=[None, 3], dtype=tf.float32) 
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) 
A = tf.Variable(tf.random_normal(shape=[3,1])) 
b = tf.Variable(tf.random_normal(shape=[1,1])) 
model_output = tf.add(tf.matmul(x_data, A), b)

1. 对于弹性网络，损失函数具有部分斜率的 L1 和 L2 范数。我们创建这些术语，然后将它们添加到损失函数中，如下所示：

elastic_param1 = tf.constant(1.) 
elastic_param2 = tf.constant(1.) 
l1_a_loss = tf.reduce_mean(tf.abs(A)) 
l2_a_loss = tf.reduce_mean(tf.square(A)) 
e1_term = tf.multiply(elastic_param1, l1_a_loss) 
e2_term = tf.multiply(elastic_param2, l2_a_loss) 
loss = tf.expand_dims(tf.add(tf.add(tf.reduce_mean(tf.square(y_target - model_output)), e1_term), e2_term), 0)

1. 现在，我们可以初始化变量，声明我们的优化函数，运行训练循环，并拟合我们的系数，如下所示：

init = tf.global_variables_initializer() 
sess.run(init) 
my_opt = tf.train.GradientDescentOptimizer(learning_rate) 
train_step = my_opt.minimize(loss) 
loss_vec = [] 
for i in range(1000): 
    rand_index = np.random.choice(len(x_vals), size=batch_size) 
    rand_x = x_vals[rand_index] 
    rand_y = np.transpose([y_vals[rand_index]]) 
    sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y}) 
    temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y}) 
    loss_vec.append(temp_loss[0]) 
    if (i+1)%250==0: 
        print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b))) 
        print('Loss = ' + str(temp_loss))

1. 这是代码的输出：

Step #250 A = [[ 0.42095602] 
 [ 0.1055888 ] 
 [ 1.77064979]] b = [[ 1.76164341]] 
Loss = [ 2.87764359] 
Step #500 A = [[ 0.62762028] 
 [ 0.06065864] 
 [ 1.36294949]] b = [[ 1.87629771]] 
Loss = [ 1.8032167] 
Step #750 A = [[ 0.67953539] 
 [ 0.102514 ] 
 [ 1.06914485]] b = [[ 1.95604002]] 
Loss = [ 1.33256555] 
Step #1000 A = [[ 0.6777274 ] 
 [ 0.16535147] 
 [ 0.8403284 ]] b = [[ 2.02246833]] 
Loss = [ 1.21458709]

1. 现在，我们可以观察训练迭代的损失，以确保算法收敛，如下所示：

plt.plot(loss_vec, 'k-') 
plt.title('Loss per Generation') 
plt.xlabel('Generation') 
plt.ylabel('Loss') 
plt.show()

我们得到上面代码的以下图：

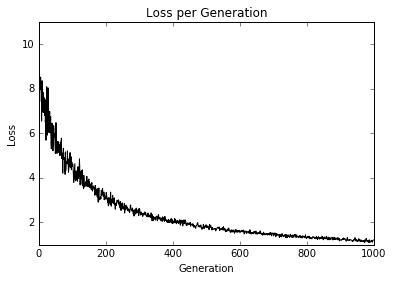
图 10：在 1,000 次训练迭代中绘制的弹性净回归损失

工作原理

这里实现弹性网络回归以及多元线性回归。我们可以看到，利用损失函数中的这些正则化项，收敛速度比先前的秘籍慢。正则化就像在损失函数中添加适当的术语一样简单。