TensorFlow 中的简单 RNN
在 TensorFlow 中定义和训练简单 RNN 的工作流程如下:
- 定义模型的超参数:
state_size = 4
n_epochs = 100
n_timesteps = n_x
learning_rate = 0.1
这里新的超参数是state_size。 state_size表示 RNN 小区的权重向量的数量。
- 为模型定义
X和Y参数的占位符。X占位符的形状为(batch_size, number_of_input_timesteps, number_of_inputs),Y占位符的形状为(batch_size, number_of_output_timesteps, number_of_outputs)。对于batch_size,我们使用None,以便我们以后可以输入任意大小的批次。
X_p = tf.placeholder(tf.float32, [None, n_timesteps, n_x_vars],
name='X_p')
Y_p = tf.placeholder(tf.float32, [None, n_timesteps, n_y_vars],
name='Y_p')
- 将输入占位符
X_p转换为长度等于时间步数的张量列表,在此示例中为n_x或 1:
# make a list of tensors of length n_timesteps
rnn_inputs = tf.unstack(X_p,axis=1)
- 使用
tf.nn.rnn_cell.BasicRNNCell创建一个简单的 RNN 单元:
cell = tf.nn.rnn_cell.BasicRNNCell(state_size)
- TensorFlow 提供
static_rnn和dynamic_rnn便利方法(以及其他方法)分别创建静态和动态 RNN。创建静态 RNN:
rnn_outputs, final_state = tf.nn.static_rnn(cell,
rnn_inputs,
dtype=tf.float32
)
静态 RNN 在编译时创建单元,即展开循环。动态 RNN 创建单元,即在运行时展开循环 。在本章中,我们仅展示了 static_rnn 的示例,但是一旦获得静态 RNN 的专业知识,就应该探索 dynamic_rnn 。
static_rnn方法采用以下参数:
cell:我们之前定义的基本 RNN 单元对象。它可能是另一种单元,我们将在本章中进一步看到。rnn_inputs:形状(batch_size, number_of_inputs)的张量列表。dtype:初始状态和预期输出的数据类型。定义预测层的权重和偏差参数:
W = tf.get_variable('W', [state_size, n_y_vars])
b = tf.get_variable('b', [n_y_vars],
initializer=tf.constant_initializer(0.0))
- 将预测层定义为密集线性层:
predictions = [tf.matmul(rnn_output, W) + b \
for rnn_output in rnn_outputs]
- 输出 Y 是 Tensors 的形状;将其转换为张量列表:
y_as_list = tf.unstack(Y_p, num=n_timesteps, axis=1)
- 将损失函数定义为预测标签和实际标签之间的均方误差:
mse = tf.losses.mean_squared_error
losses = [mse(labels=label, predictions=prediction)
for prediction, label in zip(predictions, y_as_list)
]
- 将总损失定义为所有预测时间步长的平均损失:
total_loss = tf.reduce_mean(losses)
- 定义优化器以最小化
total_loss:
optimizer = tf.train.AdagradOptimizer(learning_rate).minimize(total_loss)
- 现在我们已经定义了模型,损耗和优化器函数,让我们训练模型并计算训练损失:
with tf.Session() as tfs:
tfs.run(tf.global_variables_initializer())
epoch_loss = 0.0
for epoch in range(n_epochs):
feed_dict={X_p: X_train.reshape(-1, n_timesteps,
n_x_vars),
Y_p: Y_train.reshape(-1, n_timesteps,
n_x_vars)
}
epoch_loss,y_train_pred,_=tfs.run([total_loss,predictions,
optimizer], feed_dict=feed_dict)
print("train mse = {}".format(epoch_loss))
我们得到以下值:
train mse = 0.0019413739209994674
- 让我们在测试数据上测试模型:
feed_dict={X_p: X_test.reshape(-1, n_timesteps,n_x_vars),
Y_p: Y_test.reshape(-1, n_timesteps,n_y_vars)
}
test_loss, y_test_pred = tfs.run([total_loss,predictions],
feed_dict=feed_dict
)
print('test mse = {}'.format(test_loss))
print('test rmse = {}'.format(math.sqrt(test_loss)))
我们在测试数据上得到以下 mse 和 rmse(均方根误差):
test mse = 0.008790395222604275
test rmse = 0.09375710758446143
这非常令人印象深刻。
这是一个非常简单的例子,只用一个变量值预测一个时间步。在现实生活中,输出受到多个特征的影响,并且需要预测不止一个时间步。后一类问题被称为多变量多时间步进预测问题。这些问题是使用递归神经网络进行更好预测的积极研究领域。
现在让我们重新调整预测和原始值并绘制原始值(请在笔记本中查找代码)。
我们得到以下绘图:
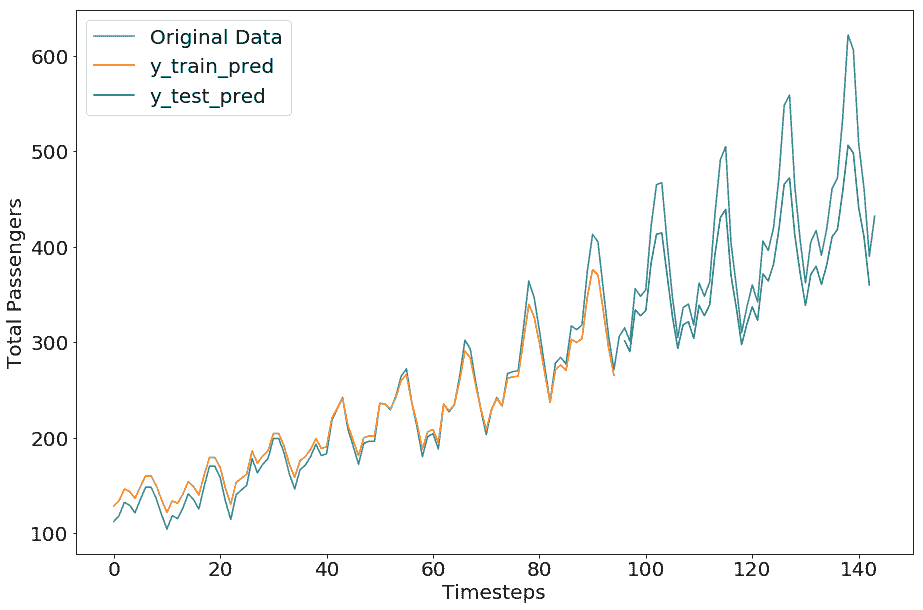
令人印象深刻的是,在我们的简单示例中,预测数据几乎与原始数据相匹配。对这种准确预测的一种可能解释是,单个时间步的预测基于来自最后一个时间步的单个变量的预测,因此它们总是在先前值的附近。
尽管如此,前面示例的目的是展示在 TensorFlow 中创建 RNN 的方法。现在让我们使用 RNN 变体重新创建相同的示例。