岭正则化

以下是岭正则化回归的完整代码，用于训练模型以预测波士顿房屋定价：

num_outputs = y_train.shape[1]
num_inputs = X_train.shape[1]

x_tensor = tf.placeholder(dtype=tf.float32,
                          shape=[None, num_inputs], name='x')
y_tensor = tf.placeholder(dtype=tf.float32,
                          shape=[None, num_outputs], name='y')

w = tf.Variable(tf.zeros([num_inputs, num_outputs]),
                dtype=tf.float32, name='w')
b = tf.Variable(tf.zeros([num_outputs]),
                dtype=tf.float32, name='b')

model = tf.matmul(x_tensor, w) + b

ridge_param = tf.Variable(0.8, dtype=tf.float32)
ridge_loss = tf.reduce_mean(tf.square(w)) * ridge_param

loss = tf.reduce_mean(tf.square(model - y_tensor)) + ridge_loss

learning_rate = 0.001
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

mse = tf.reduce_mean(tf.square(model - y_tensor))
y_mean = tf.reduce_mean(y_tensor)
total_error = tf.reduce_sum(tf.square(y_tensor - y_mean))
unexplained_error = tf.reduce_sum(tf.square(y_tensor - model))
rs = 1 - tf.div(unexplained_error, total_error)

num_epochs = 1500
loss_epochs = np.empty(shape=[num_epochs],dtype=np.float32)
mse_epochs = np.empty(shape=[num_epochs],dtype=np.float32)
rs_epochs = np.empty(shape=[num_epochs],dtype=np.float32)

mse_score = 0.0
rs_score = 0.0

with tf.Session() as tfs:
    tfs.run(tf.global_variables_initializer())
    for epoch in range(num_epochs):
        feed_dict = {x_tensor: X_train, y_tensor: y_train}
        loss_val, _ = tfs.run([loss, optimizer], feed_dict=feed_dict)
        loss_epochs[epoch] = loss_val

        feed_dict = {x_tensor: X_test, y_tensor: y_test}
        mse_score, rs_score = tfs.run([mse, rs], feed_dict=feed_dict)
        mse_epochs[epoch] = mse_score
        rs_epochs[epoch] = rs_score

print('For test data : MSE = {0:.8f}, R2 = {1:.8f} '.format(
    mse_score, rs_score))

我们得到以下结果：

For test data : MSE = 30.64177132, R2 = 0.63988018

绘制损失和 MSE 的值，我们得到以下损失图：

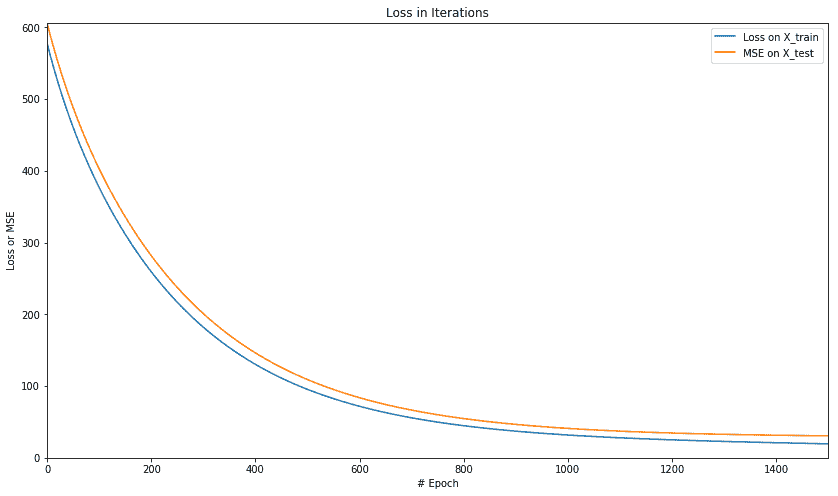
我们得到以下 R 平方图：

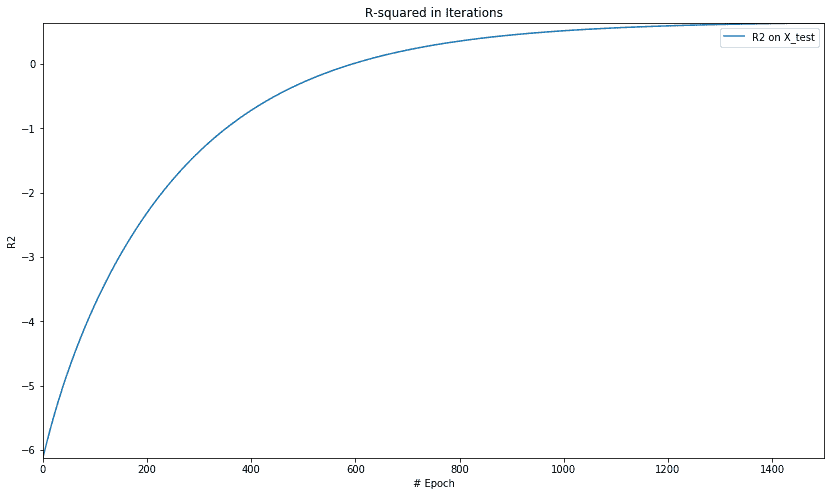
让我们来看看套索和岭正则化方法的组合。