TensorFlow 中的变分自编码器

变分自编码器是自编码器的现代生成版本。让我们为同一个前面的问题构建一个变分自编码器。我们将通过提供来自原始和嘈杂测试集的图像来测试自编码器。

我们将使用不同的编码风格来构建此自编码器，以便使用 TensorFlow 演示不同的编码风格：

1. 首先定义超参数：

learning_rate = 0.001
n_epochs = 20
batch_size = 100
n_batches = int(mnist.train.num_examples/batch_size)
# number of pixels in the MNIST image as number of inputs
n_inputs = 784
n_outputs = n_inputs

1. 接下来，定义参数字典以保存权重和偏差参数：

params={}

1. 定义每个编码器和解码器中隐藏层的数量：

n_layers = 2
# neurons in each hidden layer
n_neurons = [512,256]

1. 变分编码器中的新增加是我们定义潜变量z的维数：

n_neurons_z = 128 # the dimensions of latent variables

1. 我们使用激活tanh：

activation = tf.nn.tanh

1. 定义输入和输出占位符：

x = tf.placeholder(dtype=tf.float32, name="x", 
                    shape=[None, n_inputs]) 
y = tf.placeholder(dtype=tf.float32, name="y", 
                    shape=[None, n_outputs])

1. 定义输入层：

# x is input layer
layer = x

1. 定义编码器网络的偏差和权重并添加层。变分自编码器的编码器网络也称为识别网络或推理网络或概率编码器网络：

for i in range(0,n_layers):
    name="w_e_{0:04d}".format(i)
    params[name] = tf.get_variable(name=name, 
        shape=[n_inputs if i==0 else n_neurons[i-1],
        n_neurons[i]], 
        initializer=tf.glorot_uniform_initializer()
        )
    name="b_e_{0:04d}".format(i)
    params[name] = tf.Variable(tf.zeros([n_neurons[i]]),
        name=name
        )
    layer = activation(tf.matmul(layer,
        params["w_e_{0:04d}".format(i)]
        ) + params["b_e_{0:04d}".format(i)]
        )

1. 接下来，添加潜在变量的均值和方差的层：

name="w_e_z_mean"
params[name] = tf.get_variable(name=name,
    shape=[n_neurons[n_layers-1], n_neurons_z],
    initializer=tf.glorot_uniform_initializer()
    )
name="b_e_z_mean"
params[name] = tf.Variable(tf.zeros([n_neurons_z]),
    name=name
    )
z_mean = tf.matmul(layer, params["w_e_z_mean"]) + 
            params["b_e_z_mean"]
name="w_e_z_log_var"
params[name] = tf.get_variable(name=name,
    shape=[n_neurons[n_layers-1], n_neurons_z],
    initializer=tf.glorot_uniform_initializer()
    )
name="b_e_z_log_var"
params[name] = tf.Variable(tf.zeros([n_neurons_z]),
    name="b_e_z_log_var"
    )

z_log_var = tf.matmul(layer, params["w_e_z_log_var"]) + 
            params["b_e_z_log_var"]

1. 接下来，定义表示与z方差的变量相同形状的噪声分布的 epsilon 变量：

epsilon = tf.random_normal(tf.shape(z_log_var), 
    mean=0, 
    stddev=1.0,
    dtype=tf.float32, 
    name='epsilon'
    )

1. 根据均值，对数方差和噪声定义后验分布：

z = z_mean + tf.exp(z_log_var * 0.5) * epsilon

1. 接下来，定义解码器网络的权重和偏差，并添加解码器层。变分自编码器中的解码器网络也称为概率解码器或生成器网络。

# add generator / probablistic decoder network parameters and layers
layer = z

for i in range(n_layers-1,-1,-1):
name="w_d_{0:04d}".format(i)
    params[name] = tf.get_variable(name=name, 
    shape=[n_neurons_z if i==n_layers-1 else n_neurons[i+1],
    n_neurons[i]], 
    initializer=tf.glorot_uniform_initializer()
    )
name="b_d_{0:04d}".format(i)
params[name] = tf.Variable(tf.zeros([n_neurons[i]]),
    name=name 
    )
layer = activation(tf.matmul(layer, params["w_d_{0:04d}".format(i)]) + 
    params["b_d_{0:04d}".format(i)])

1. 最后，定义输出层：

name="w_d_z_mean"
params[name] = tf.get_variable(name=name,
    shape=[n_neurons[0],n_outputs],
    initializer=tf.glorot_uniform_initializer()
    )
name="b_d_z_mean"
    params[name] = tf.Variable(tf.zeros([n_outputs]),
    name=name
    )
name="w_d_z_log_var" 
params[name] = tf.Variable(tf.random_normal([n_neurons[0],
    n_outputs]),
    name=name
    )
name="b_d_z_log_var"
params[name] = tf.Variable(tf.zeros([n_outputs]),
    name=name
    )
layer = tf.nn.sigmoid(tf.matmul(layer, params["w_d_z_mean"]) + 
    params["b_d_z_mean"])

model = layer

1. 在变异自编码器中，我们有重建损失和正则化损失。将损失函数定义为重建损失和正则化损失的总和：

rec_loss = -tf.reduce_sum(y * tf.log(1e-10 + model) + (1-y) 
                            * tf.log(1e-10 + 1 - model), 1)
reg_loss = -0.5*tf.reduce_sum(1 + z_log_var - tf.square(z_mean) 
                                - tf.exp(z_log_var), 1) 
loss = tf.reduce_mean(rec_loss+reg_loss)

1. 根据AdapOptimizer定义优化程序函数：

optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
            .minimize(loss)

1. 现在让我们训练模型并从非噪声和噪声测试图像生成图像：

with tf.Session() as tfs:
    tf.global_variables_initializer().run()
    for epoch in range(n_epochs):
        epoch_loss = 0.0
        for batch in range(n_batches):
            X_batch, _ = mnist.train.next_batch(batch_size)
            feed_dict={x: X_batch,y: X_batch}
            _,batch_loss = tfs.run([optimizer,loss], 
                            feed_dict=feed_dict)
            epoch_loss += batch_loss
        if (epoch%10==9) or (epoch==0):
            average_loss = epoch_loss / n_batches
            print("epoch: {0:04d} loss = {1:0.6f}"
                      .format(epoch,average_loss))

# predict images using autoencoder model trained
Y_test_pred1 = tfs.run(model, feed_dict={x: test_images})
Y_test_pred2 = tfs.run(model, feed_dict={x: test_images_noisy})

我们得到以下输出：

epoch: 0000   loss = 180.444682
epoch: 0009   loss = 106.817749
epoch: 0019   loss = 102.580904

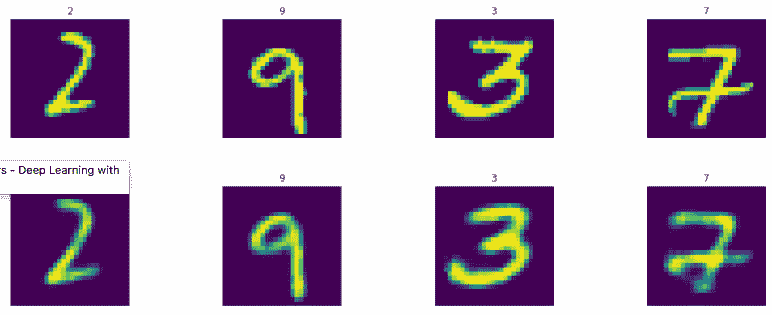
现在让我们显示图像：

display_images(test_images.reshape(-1,pixel_size,pixel_size),test_labels)
display_images(Y_test_pred1.reshape(-1,pixel_size,pixel_size),test_labels)

结果如下：

display_images(test_images_noisy.reshape(-1,pixel_size,pixel_size),
    test_labels)
display_images(Y_test_pred2.reshape(-1,pixel_size,pixel_size),test_labels)

结果如下：

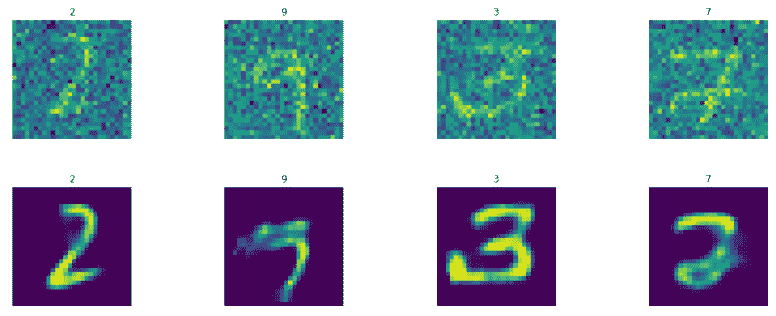
同样，可以通过超参数调整和增加学习量来改善结果。