Keras 中的栈式自编码器

现在让我们在 Keras 中构建相同的自编码器。

我们使用以下命令清除笔记本中的图，以便我们可以构建一个新图，该图不会占用上一个会话或图中的任何内存：

tf.reset_default_graph() keras.backend.clear_session()

1. 首先，我们导入 keras 库并定义超参数和层：

import keras
from keras.layers import Dense
from keras.models import Sequential

learning_rate = 0.001
n_epochs = 20
batch_size = 100
n_batches = int(mnist.train.num_examples/batch_sizee
# number of pixels in the MNIST image as number of inputs
n_inputs = 784
n_outputs = n_i
# number of hidden layers
n_layers = 2
# neurons in each hidden layer
n_neurons = [512,256]
# add decoder layers:
n_neurons.extend(list(reversed(n_neurons)))
n_layers = n_layers * 2

1. 接下来，我们构建一个顺序模型并为其添加密集层。对于更改，我们对隐藏层使用relu激活，为最终层使用linear激活：

model = Sequential()

# add input to first layer
model.add(Dense(units=n_neurons[0], activation='relu', 
    input_shape=(n_inputs,)))

for i in range(1,n_layers):
    model.add(Dense(units=n_neurons[i], activation='relu'))

# add last layer as output layer
model.add(Dense(units=n_outputs, activation='linear'))

1. 现在让我们显示模型摘要以查看模型的外观：

model.summary()

该模型在五个密集层中共有 1,132,816 个参数：

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_1 (Dense)              (None, 512)               401920    
_________________________________________________________________
dense_2 (Dense)              (None, 256)               131328    
_________________________________________________________________
dense_3 (Dense)              (None, 256)               65792     
_________________________________________________________________
dense_4 (Dense)              (None, 512)               131584    
_________________________________________________________________
dense_5 (Dense)              (None, 784)               402192    
=================================================================
Total params: 1,132,816
Trainable params: 1,132,816
Non-trainable params: 0
_________________________________________________________________

1. 让我们用上一个例子中的均方损失编译模型：

model.compile(loss='mse',
    optimizer=keras.optimizers.Adam(lr=learning_rate),
    metrics=['accuracy'])

model.fit(X_train, X_train,batch_size=batch_size,
    epochs=n_epochs)

在 20 个周期，我们能够获得 0.0046 的损失，相比之前我们得到的 0.078550：

Epoch 1/20
55000/55000 [==========================] - 18s - loss: 0.0193 - acc: 0.0117    
Epoch 2/20
55000/55000 [==========================] - 18s - loss: 0.0087 - acc: 0.0139 
...
...
...   
Epoch 20/20
55000/55000 [==========================] - 16s - loss: 0.0046 - acc: 0.0171

现在让我们预测并显示模型生成的训练和测试图像。第一行表示实际图像，第二行表示生成的图像。以下是 t 降雨设置图像：

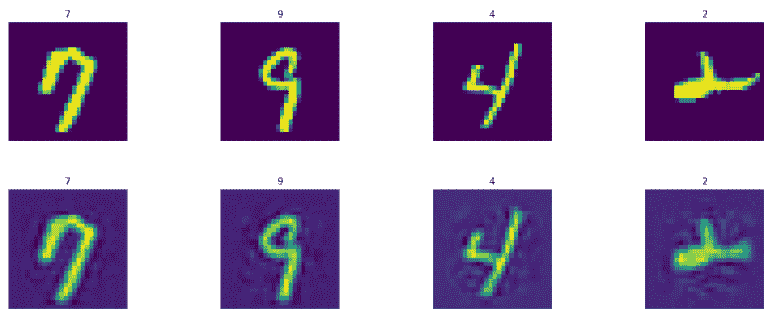
以下是测试集图像：

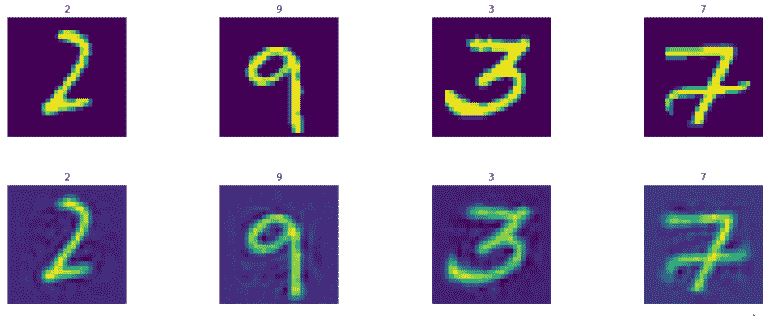
这是我们在能够从 256 个特征生成图像时实现的非常好的准确性。