大家好，这是我加入

大家好，这是我加入星球的第27次分享，请大家多多指教

《多元思维模型NO.24－－决策树模型》

毕业后10年的同学聚会，各自的选择不同，价值观不同。 有的人商业顺风顺水、大富大贵 有的人仕途平步青云，扶摇直上 有的人看破红尘，皈依佛门 有的人无所适从，一成不变，只是重复以前的自己。

当时的起步都在一个起跑线上，为什么过了10年就发生了这 么大的变化，可能就是当初的一个选择，造就了现在不同的 结果。

那有没有一个思维模型可以帮助我们做出正确的选择？ 顶级的高手都喜欢使用的一款思维模型：决策树模型。

1.决策数模型的定义

决策树(Decision Tree）是在已知各种情况发生概率的基础 上，通过构成决策树来求取净现值的期望值大于等于零的概 率，评价项目风险，判断其可行性的决策分析方法，是直观 运用概率分析的一种图解法。由于这种决策分支画成图形很 像一棵树的枝干，故称决策树。

在机器学习中，决策树模型是一个预测模型，他代表的是对 象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱 程度，使用算法ID3,C4.5和C5.0生成树算法使用熵。这一度量 是基于信息学理论中熵的概念。

决策树是一种树形结构，其中每个内部节点表示一个属性上 的测试，每个分支代表一个测试输出，每个叶节点代表一种 类别。

决策树模型是一种十分常用的分类方法。他是一种监管学 习，所谓监管学习就是给定一堆样本，每个样本都有一组属 性和一个类别，这些类别是事先确定的，那么通过学习得到 一个分类器，这个分类器能够对新出现的对象给出正确的分 类。这样的机器学习就被称之为监督学习。

二.决策树模型的详细解释 芒格说：“这么多年来，我一直跟巴菲特同事，他拥有许多优

点，其中之一就是它能够自动地根据决策树理论和基本的排

列组员原理来思考问题。”

费马和帕斯卡的努力，标志着概率论的诞生，而概率是风险 管理和决策理论的基础。

之前还提到过条件概率和贝叶斯定理模型，可能讲得有些复 杂，但是原理很简单，就是“当信息更新之后，我们的结论的 概率也发生了变化。”

用公式描述就是：初始概率 & 新的信息 = 新的概率 举一个例子：假设人类患某种癌症的概率是0.08%，现在最先

进的技术检测患这种癌的正确率是99%，如果小明检测患这

种癌，那么他患这种癌症的概率是多少？

直觉会认为检测患这种癌的正确率是99%，那么他患这种癌 症的概率应该是99%。

但是正确的方式是：0.08%（初始概率） & 99%（新信息）， 最后的结果是7.34%，远低于直觉的99%。计算方法在贝叶斯 定理模型这篇文章有讲到。

如果这个例子比较难理解，那我们换一个。 我们知道掷骰子出现3的概率是1/6，这时候多了一个信息，点

数是奇数，那么概率就变成了1/3。

初始概率 & 新的信息 = 新的概率

（1/6） & （是奇数） = 1/3

假设这时又多了一个信息，点数为“小”，那么概率就变成了

1/2。

贝叶斯的分析方法就是不断把新的信息加入到推理和决策的 过程，也就是本文要讲的决策树模型。

决策树模型是一种在不完全信息情况下，帮助我们做出更高 概率正确决策的思考工具。

用决策树模型其实也很简单，主要三个步骤：

1、画决策树（画出分支）

2、分析各种几率和收益损失

3、反向求解（ 从末端开始向前推导，确认每个分支的价值， 然后在每个结点处找出自己应该做的选择）。

决策树模型的4个作用：

1、帮助我们选择平均回报最高的决策，

2、根据别人的选择推测他人对事件发生几率的预测。

3、推测价值，或是别人认为的价值。

4、判断信息价值。 三.决策树模型的场景应用

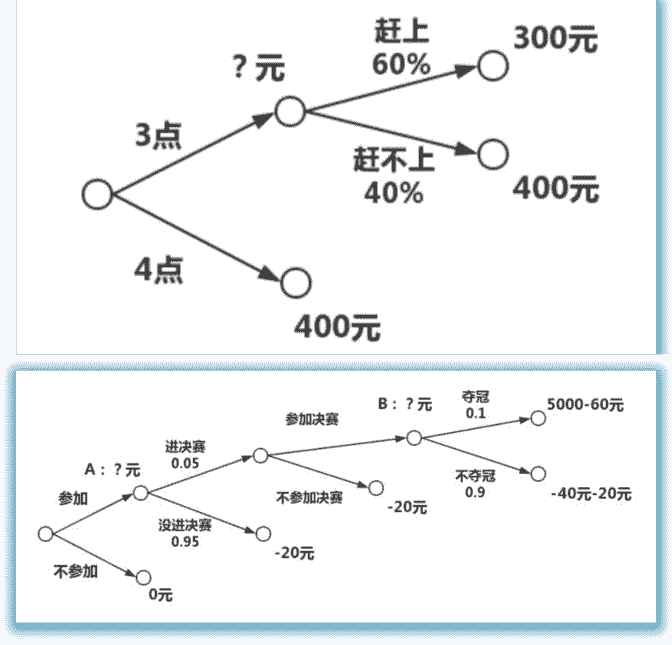
1.帮助我们选择平均回报最高的决策。 案例1：一次分叉决策树。 假设现在2点，你要去做火车，3点的票200元，但是40%的概

率赶不上，4点的票400元。应该怎么买？

按照之前的方法，可以算一下期望，买3点的票期望：

=0.6200+0.4600=360元，比400少，应该买三点的票。画成 决策树就是（见文末）：

？位置的数值，由两个分支结点可以算出来为360元。所以选

3点的票，更高概率能省钱。

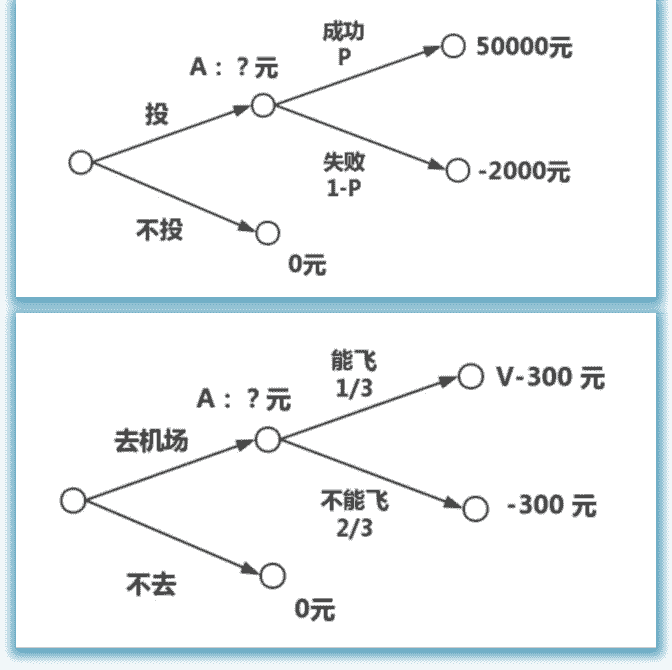
案例2：两次分叉决策树。 现在你想要参加一场比赛，奖金有5000元。有初选和决赛两

个环节。

初选，200人参加，报名费20元。 决赛，10人进决赛，需要40元准备材料。 假设每个人的概率都相同，你应该参加初选和决赛么？ 初选200人，所以参加初选进决赛的概率=1/200=0.05，没进的

概率0.9。

决赛10人，所以参加决赛夺冠的概率=0.1，收益5000-60元， 没夺冠的概率0.9，损失等于两次费用60元。

决策树（见文末）：

可以先算出参加决赛的期望：B = 0.14940 - 0.960=440，对 比损失20元，应该参加决赛。

然后可以算出参加初赛的期望：A = 0.05&440 - 0.95*20=3， 应该参加初赛。

如果参赛的人再多一点点，比如250人，初赛胜出概率变成

0.04，期望A的结果就变成了-1.6。这时候就不该应参与了。

所以决策树的本质是让我们更方便计算期望，从而更好的做 出更高概率正确的决策。

而期望也是概率决策理论中最基础，也最重要的概念。 巴菲特说：“用亏损的概率乘以可能亏损的金额，再用盈利概

率乘以可能盈利的金额，最后用后者减去前者。

这就是我们一直试图做的方法。这种算法并不完美，但事情 就这么简单。”

2.根据别人的选择推测他人对事件发生几率的预测。 假设一支股票需要投入2000元，预期回报50000元。

假设一个人已经投了，可以算出他对成功概率的想法。

假设投资成功的概率是P，那么失败的概率是（1-P）。还是 用决策树（见文末）：

既然一个投资了，那么他至少认为投资的期望应该大于0， 即，投的期望 A = 50000P-2000（1-P）> 0

所以P > 4%。

所以投的人认为投资成功的概率应该大于4%。

3.推测价值，或是别人认为的价值。 这个案例很有意思，可以推测你的男朋友认为见你这件事值

多少钱。

假设你的男朋友有一张候补机票去看你，他通过航空公司知 道：

1/3概率能飞；

2/3飞不了。 通过他去不去机场，就能判断他认为见你这件事值多少钱。 假设他认为看你的价值为G(irl)，坐车各种花费为300元。

先画出决策树（见文末）：

如果他不去机场，可以认为他觉得A < 0。 A = (1/3)(V-300)-(2/3)300>0

V < 900元。

所以如果他不去的话，可以认为他觉得见你不值900元。 所以 你知道该怎么做了吧。

4.判断信息价值。

我们知道通过新的信息可以提高判断的概率，如果一个新信 息能够做到这点，我们就说这条信息是有价值的，而且这个 价值可以计算出来。

信息的价值 = 得到信息的期望 - 没有信息的期望 假设现在买大小，每次下注20元，买中点数获得120元。 假设现在有人可以告诉你信息是奇数、还是偶数，要价15

元，你是否应该买这条信息？

没有新信息的期望：120(1/6)-20 = 0 得到新信息的期望：120(1/3)-20 = 20 元。 这条信息的价值：20元。所以15元买这条信息，理论上是划

算的，可以买。

当然很多时候，概率并不是这么明显可以知道的，所以相应 的决策也会更复杂。而且很多时候还需要考虑其他因素，有 时候只知道期望是不够的。但是用决策树模型作为决策参 照，会比凭感觉要靠谱得多。

查理芒格说：“掌握排列组合原理并不难，真正困难的是在日 常生活中习惯于几乎每天都应用它。”

决策树模型也一样，看懂上面这些例子并不难，真正困难的 是在日常生活中习惯于几乎每天都应用它。每个人每天做决 策的次数都很多，其中一两次拿出来试试用决策树的方法来 思考，也许就能打开一片新的世界。

2019-01-31(20赞)

评论区：

大叔是大树 : 有联系方式嘛？想和你探讨算法 link : 最近事比较多，等忙完吧

陈亦非 : 有软件吗

朱小峰 : Day81

关注公众号"懒人找资源"，星球资源一站式服务